
ТВ_и_МС
.pdf
Случайные величины |
33 |
Рассмотрим элементарный участок dx. Вероятность попадания случайной величины Х на этот участок dx (с точностью до бесконечно малых высших порядков) равна ƒ(x)dx=dF(x).
Величина ƒ(х)dx называется элементом вероятности для точки. Геометрически - это площадь заштрихованной области. Рассмотрим вероятность попадания случайной величины Х на участок от α до β. Эта вероятность равна сумме элементов вероятности на этом участке, т.е. определенному
β
интегралу: P{α < X < β} = ∫ f (x)dx .
α
На рисунке заштрихованная область.
|
F( x ) = P{ X < x } = P{ −∞ < X < x } = ∫x |
f ( x )dx . |
|
−∞ |
|
Свойства плотности распределения: |
|
|
1. |
ƒ(x)≥0; |
|
2. |
∞∫ f ( x )dx =1. |
|
|
−∞ |
|
Пример:
Функция распределения непрерывной случайной величины Х задана выражением
0, при x ≤ 0, F(x)= x2 , при 0<x ≤1,
1, при 1<x
Найти:
1.Плотность распределения ƒ(х) случайной величины Х и построить ее граграфик;
2.Найти вероятность того, что случайная ве-
личина Х в результате опыта примет значение между 0,25 и 0,5.
1) |
|
0, при x ≤ 0, |
f (x) = F '(x) = |
|
|
|
2x, при 0 < x <1, |
|
|
|
|
|
|
0, при x >1 |
или ƒ(x)= 2x при 0<x<1.
2) Вероятность попадания случайной величины
Х на участок (0,25;0,5): P{ 0,25 < X < 0,5 } = 0∫,5 f ( x )dx , но можно воспользо-
0,25
ваться формулой: P{0,25<X<0,5}= F(0,5)-F(0,25)=0,52-0,252=0,1875.
34 |
Лекции 3-5 |
3.4.Числовые характеристики случайных величин
Втеории вероятностей числовые характеристики играют огромную роль. С их помощью существенно облегчается решение многих задач. Среди числовых характеристик случайной величины рассмотрим сначала характеристику положения, фиксирующую положение случайной величины на числовой оси, т.е. некоторое среднее, ориентировочное значение случайной величины, около которого группируются ее возможные значения. Такой характеристикой является математическое ожидание, иногда ее называют средним значением случайной величины.
3.4.1. Математическое ожидание
ОМатематическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности
этих значений.
M(X )= ∑xi pi = mx
i=1n
Пример:
Дано распределение случайной величины. Найти М(Х).
|
X |
2 |
3 |
4 |
5 |
|
M (X |
P |
0,1 |
0,2 |
0,2 |
0,5 |
|
)= m(x)= |
2 0,1 + |
3 0,2 + 4 0,2 + 5 0,5 = 4,1. |
||||
!При достаточно большом числе опытов можно среднее арифметическое наблюденных значений случайной величины принимать приближенно равным ее математическому ожиданию.
Свойства математического ожидания:
1.М(с)=с, с- константа;
2.М(сХ)=сМ(Х).
ОМатематическим ожиданием непрерывной случайной величины Х с
плотностью ƒ(х) называется величина mx = M (X )= ∞∫ x f (x)dx .
−∞
Пример:
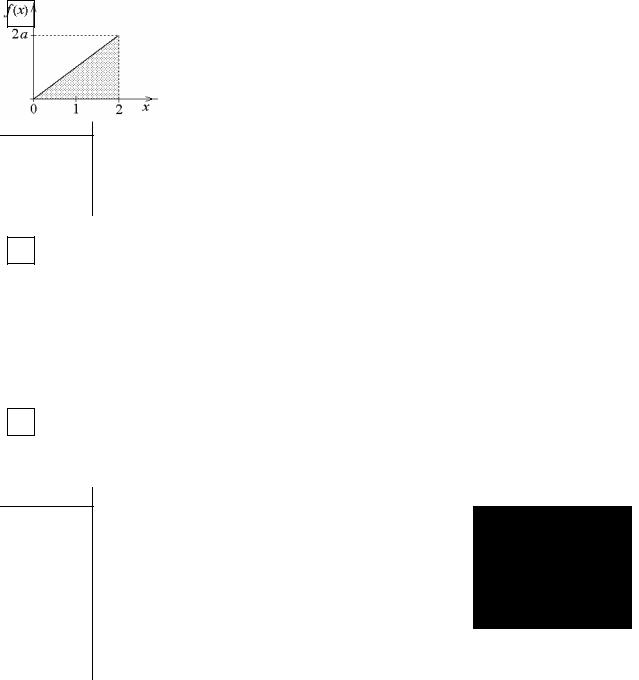
Непрерывная случайная величина Х распределена на участке (0,2) с плотностью распределения ƒ(x)=ax при x (0,2). Найти коэффициент а и математическое ожидание mx
Решение:
Построим график ƒ(x).
коэффициент а найдем из условия, что S∆=1. S∆ = 12 2 2a =1. Следовательно, a = 12 .

Случайные величины |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35 |
|
|
mx = |
2 |
x |
1 |
x dx = |
1 |
2 |
x2dx = |
1 x3 |
|
2 |
= |
8 |
= |
4 |
≈1,33 . |
||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
∫ |
|
|
∫ |
|
|
|
|
|
|
|
||||||||
2 |
2 |
2 3 |
|
|
|
6 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3.4.2. Дисперсия. Среднее квадратическое отклонение
Характеристикой отклонений случайной величины от ее математического ожидания является дисперсия, описывающая рассеяние случайной величины относительно среднего значения.
ОДисперсией случайной величины Х D(x)=Dx называется Dx=M((X-Mx)2), где разность X-Mx называется отклонением случайной величины Х от ее математического ожидания.
Для непосредственного вычисления дисперсии служат формулы:
n
Dx = ∑( xi − mx )2 pi – для дискретной случайной величины,
i=1
Dx = ∞∫(x − mx )2 f ( x )dx – для непрерывной случайной величины.
−∞
На практике пользуются формулой: Dx=M(X2)-(M(X))2, т.е. дисперсия случайной величины равна математическому ожиданию ее квадрата минус квадрат математического ожидания. Она получается из определения:
Dx = M ((X − Mx )2 )= M (X 2 −2X Mx + Mx2 )=
=M (X 2 )− 2M (X M x )+ M (M x2 )=
=M (X 2 )− 2M x M x + M x2 = M (X 2 )− M x2 .
Свойства дисперсии:
1.Dx≥0;
2.Dс=0;
3.D(cx)=c2Dx;
4.D(X+Y)=DX+DY (X,Y-независимые случайные величины);
5.D(C+X)=DX.
Пример:
В техническом устройстве работают независимо 2 блока. Вероятность безотказной работы первого блока p1=0,4, второго – p2=0,7. Случайная величина Х
– число работающих блоков. Найти ее математическое ожидание и дисперсию.
Решение: Случайная величина Х принимает значения 0, 1, 2. Вероятности этих значений: P{X=0}=0,6·0,3=0,18; P{X=1}=1-(0,18+0,28)=0,54; P{X=2}=0,4·0,7=0,28.
Ряд распределения случайной величины Х:
X |
0 |
1 |
2 |
P |
0,18 |
0,54 |
0,28 |
mx=0·0,18+1·0,54+2·0,28=1,1.
Дисперсия Dx=M(X2)-(M(X))2,

36 |
Лекции 3-5 |
(M(X))2=(1,1)2=1,21,
Найдем M(X2)=02·0,18+12·0,54+22·0,28=1,66. Dx=1,66-1,21=0,45.
Дисперсия имеет размерность квадрата случайной величины. Для наглядности в качестве характеристики рассеивания удобнее пользоваться числом, размерность которого совпадает с размерностью случайной величины.
Величина Dx =σx называется средним квадратическим отклонением
случайной величины (с.к.о.).
Для сравнения различных случайных величин бывает удобно привести их к стандартному виду: начало отсчета перенести в точку, совпадающую с математическим ожиданием с.в., а масштаб выбрать так, чтобы в новых единицах с.к.о. было равно единице.
О Случайная величина Y = |
X − MX |
называется стандартной случайной |
|||||||||
σx |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
величиной, соответствующей случайной величине X . |
|
|
|
||||||||
|
X − MX |
|
MX − MX = 0 , |
|
X − MX |
|
DX |
|
|
||
MY = M |
= |
DY = D |
= |
|
=1. |
||||||
σx |
σx |
(σx ) |
2 |
||||||||
|
|
σx |
|
|
|
|
|||||
3.4.3. Мода, медиана, квантили
Кроме математического ожидания в качестве характеристики положения применяют моду и медиану случайной величины.
ОМода дискретной случайной величины – это наиболее вероятное значение случайной величины; для непрерывной случайной величины – это точка максимума плотности распределения. Обозначение: Мoх.
Пример:
 На рисунке представлен многоугольник распределения. Для данной дискретной случайной величины Х мода Мoх =2.
На рисунке представлен многоугольник распределения. Для данной дискретной случайной величины Х мода Мoх =2.
Для непрерывной случайной величины на рисунке представлена кривая распределения случайной величены. Мoх – точка, в которой плотность распределения ƒ(х) имеет максимум.
Мода может быть не единственной. Такое распределение называется полимодальным. В этом случае часто статистический материал, использованный в исследованиях, является разнородным.
Случайные величины |
37 |
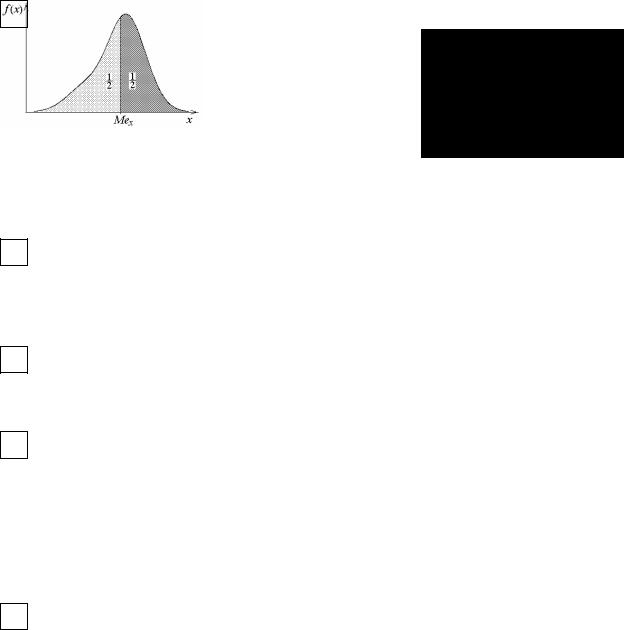
ОМедиана Мeх случайной величиныэто такое значение случайной величины, для
которого P{X < xm}= P{X > xm}= 12 . Медиана является характеристикой непрерывных случайных величин. Геометрически медианаэто точка на оси 0x для которой площади под графиком плотности распределения, лежащие слева и справа от нее, одинаковы и равны 12 .
! Если плотность распределения симметрична относительно прямой x = a и распределение одномодально, то матожидание, медиана и мода совпадают между собой,
M(x) = Mex = Мoх.
В приложениях часто используются квантили различных распределений.
ОКвантилью уровня p qp случайной величины X называется решение уравнения F (qp )= p , где F (x) – функция распределения случайной величины X, p – некоторое число, 0 < p <1.
!Медиана распределения является квантилью уровня 0,5: Mex = q0,5 .
3.4.4. Моменты случайных величин
Кроме характеристик положения случайных величин в теории вероятностей используют другие числовые характеристики – начальные и централь-
ные моменты.
ОНачальным моментом s-ого порядка случайной величины Х называет-
ся число αs (X ), равное математическому ожиданию случайной величи-
ны: Xs:αs (X )= M (X s ).
n |
|
Если Х - дискретная случайная величина, то αs (X )= ∑xis pi , где |
xi - |
i=1 |
|
значения, которые принимает случайная величина Х, pi - соответствую-
щие вероятности.
∞
Если Х – непрерывная случайная величина, то αs (X ) = ∫ xs f (x)dx , где
−∞
ƒ(х) – плотность распределения.
Если положить s =1, то первый начальный момент
n |
∞ |
α1 (X )= ∑xi pi , |
α1 (X )= ∫ xf (x)dx |
i=1 |
−∞ |

38 |
Лекции 3-5 |
|
|
|
есть математическое ожидание случайной величины Х, таким образом |
|
|
mx =α1 (X ). |
|
|
ο |
|
О |
|
|
Центрированной случайной величиной X называется отклонение |
|
|
|
ο |
|
|
случайной величины от ее математического ожидания: X = X − mx . |
!Центрирование случайной величины означает перенос начала коор-
динат в точку mx .
ОЦентральными моментами называются моменты центрированной случайной величины, (аналог моментов относительно центра массы в механике).
ОЦентральным моментом порядка s случайной величины Х называется
ο s |
s |
). |
|
|
|
|
величина µs (X )= M X |
= M ((X − mx ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
s |
Если Х – дискретная случайная величина, то |
µs |
= ∑(xi − mx ) pi ; |
||||
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
s |
если Х – непрерывная случайная величина, то |
µs |
= ∞∫(x − mx ) f (x)dx . |
||||
−∞
Кроме рассмотренных выше начальных и центральных моментов, иногда используют так называемые абсолютные моменты (начальные и центральные), определяемые как
|
s |
(X )= M |
( |
|
s |
) |
|
|
s |
|
|
ο |
|
s |
( |
|
|
x |
|
s |
) |
|
||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
β |
X |
, |
ν |
|
|
X |
|
|
|
X |
− m |
|
. |
|||||||||||
|
|
|
|
(X )= M |
|
|
|
= M |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Связь между начальными и центральными моментами |
|
|
|
|
|
|
||||||||||||||||||
Если положить S=1, то центральный момент 1-ого порядка |
|
|
|
|
|
|||||||||||||||||||
|
|
|
µ = M |
X = M (X − m )= 0 . |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
ο |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
Второй центральный момент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
ο 2 |
n |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
µ2 = M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
X |
|
= ∑(xi − mx ) pi = |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
∑xi2 pi − 2mx ∑xi pi + mx2 ∑pi =α2 − 2mx2 + mx2 =α2 − mx2 , |
|
|||||||||||||||||||||||
i=1 |
|
i=1 |
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.к. α2 = M (X 2 ), то второй центральный момент µ2 = M (X 2 )−(M (X ))2 есть
дисперсия случайной величины. Для непрерывной случайной величины

Случайные величины |
|
|
39 |
|
|
|
2 |
|
|
|
µ2 = Dx = ∞∫(x − mx ) f (x)dx = |
|
|
|
−∞ |
= ∞∫ x2 f (x)dx − 2 ∞∫ xmx f (x)dx + ∞∫ mx2 f (x)dx = =α2 − 2mxmx + mx2 =α2 − mx2 . |
|||
−∞ |
|
−∞ |
−∞ |
Аналогично для центрального момента 3-го порядка (формула куба раз- |
|||
ности), имеем |
|
|
|
D |
|
n |
− mx )3 pi =α3 −3α2mx + 2mx3 и т.д. для µ4 ,µ5 ... |
µ3 = M X 3 |
|
= ∑( xi |
|
|
|
i=1 |
|
В теории вероятностей из числовых характеристик чаще всего применяется математическое ожидание mx , дисперсия Dx или среднеквадратическое
отклонение σx . Они характеризуют самые важные черты распределения, его
3σx |
3σx |
mx
положение и степень разбросанности.
Если необходимо узнать диапазон возможных значений случайных величин, можно воспользоваться «правилом трех сигм» (доказательство дальше). Это правило гласит: Значения случайной величины Х практически не выходят за пределы интервала mx ±3σx .
Для более детального описания распределения служат моменты высших порядков.
Если многоугольник распределения дискретной случайной величины или плотность распределения непрерывной случайной величины симметричны относительно прямой x = mx , т.е. если распределение вероятностей слу-
чайной величины симметрично относительно математического ожидания случайной величины, то все центральные моменты нечетного порядка равны нулю:
|
|
µ2s+1 = 0, s =1,2,... . |
Действительно, |
при симметричном распределении и нечетном s |
|
n |
s |
|
µs = ∑(xi − mx ) pi - |
число положительных слагаемых в сумме равно числу |
|
i=1
отрицательных слагаемых (слагаемые равны по абсолютной величине) и они взаимно уничтожаются. (Для непрерывной случайной величины имеем интеграл, от нечетной функции в симметричных пределах, равный нулю).
В качестве характеристики асимметрии распределения выбран центральный момент 3-го порядка-µ3.
40 |
|
|
|
|
|
|
|
Лекции 3-5 |
µ3 |
|
|
0 |
3 |
=α3 |
−3α2mx |
+ 2mx3 , |
|
= M |
|
X |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
размерность которого [X ]3 . Для удобства используют безразмерную величину – ко-
эффициент асимметрии As = Sk = µ3 (от
σx3
английского skew – косой).
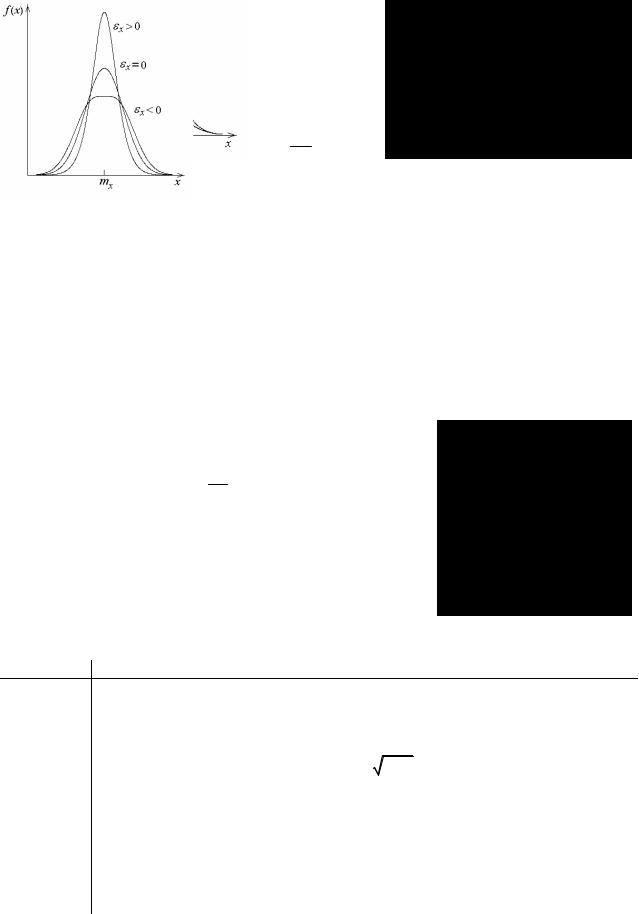
На рисунке имеем две асимметричных кривых распределения. I) – кривая с положительной асимметрией, As > 0 , II) – с отрицательной асимметрией, As < 0 .
В качестве характеристики большей или меньшей степени «сглаженности» плотности или многоугольника распределения по сравнению с нормальной плотностью (определение которой будет дано позже) используют понятие эксцесса, т.е. характеристикой островершинности или плосковершинности распределения является четвертый центральный момент - µ4, эксцесс
ε |
x |
= |
µ4 |
−3 . |
|
|
|||||
|
|
σ |
4 |
|
|
Число 3 связано |
с |
x |
часто встречающимся |
||
|
|||||
нормальным распределением, для него эксцесс
εx = 0 , σµ44 = 3 .
x
Для кривых распределения, имеющих более острую вершину, чем нормальные, эксцесс положителен, для более плосковершинных – отрицателен (см. рисунок).
Характеристика εх служит в основном для симметричных распределений.
Пример:
В предыдущей лекции рассматривались 2 независимо работающих блока. Вероятность безотказной работы первого и второго p1=0,4, p2=0,7.
Были найдены числовые характеристики случайной величины X – числа работающих блоков: математическое ожидание mx=1,1 и дисперсия Dx=0,45,
среднеквадратическое отклонение σx = |
0,45 = 0,67 . |
|||
Третий центральный момент |
|
|
|
|
3 |
3 |
|
|
|
µ3 =∑(xi −mx ) pi =(0−1,1)3 0,18+(1−1,1)3 0,54+(2−1,1)3 0,28 =0,1595, |
||||
i=1 |
|
0,1595 |
|
|
коэффициент асимметрии As = |
|
> 0 , т.е. ряд распределения имеет по- |
||
(0,67)3 |
|
|||
|
|
|
|
|
ложительную асимметрию.
Случайные величины |
41 |
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
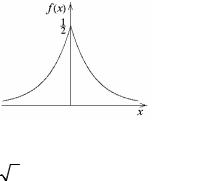
Непрерывная случайная величина Х распределена по закону Лапласа |
|||||||||||||||||||||||||
|
f (x)= |
1 e− |
|
x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти: математическое ожидание, дисперсию, среднее квадратическое от- |
|||||||||||||||||||||||||
|
клонение, асимметрию и эксцесс случайной вели- |
|||||||||||||||||||||||||
|
чины Х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∞ |
1 |
|
|
|
|
− |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
mx = |
x |
|
|
e |
|
|
|
dx = 0 , т.к. |
интеграл в |
симмет- |
|
|
|||||||||||||
|
−∞∫ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ричных пределах от нечетной функции равен ну- |
|
|
|||||||||||||||||||||||
|
лю. |
|
|
|
|
|
|
|
|
|
|
= ∞ 1 x2 e− |
|
|
|
|
dx = 2 1 ∞ x2 e−xdx = 2 ; |
|
|
|||||||
|
Дисперсия: |
|
|
|
|
|
D |
|
|
x |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
−∞∫ 2 |
|
|
|
|
|
|
|
2 ∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
среднее квадратическое отклонение σx |
= 2 ; коэффициент асимметрии |
||||||||||||||||||||||||
|
Sk=0, т.к. распределение симметрично относительно математического ожи- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ 1 |
4 |
|
|
|
−x |
|
µ4 |
|
|
|
|||
|
дания. Эксцесс: |
|
|
µ4 = 2∫0 2 x |
|
|
|
e |
|
dx = 24 ; εx |
= |
|
−3 = 3 . |
|||||||||||||
|
|
|
|
|
|
|
σx4 |
|||||||||||||||||||
4.1.Основные законы распределения случайных величин и их числовые характеристики
Вернемся к ранее рассмотренным распределениям – биномиальному и пуассоновскому и найдем их числовые характеристики, а также рассмотрим наиболее часто встречающиеся непрерывные распределения.
4.1.1. Биномиальное распределение
Ряд распределения случайной величины, подчиняющейся биномиальному закону, имеет вид:
X |
0 |
1 |
2 |
… |
k |
… |
n |
p |
qn |
Cn1 pqn−1 |
Cn2 p2qn−2 |
… |
Cnk pk qn−k |
… |
pn |
Используя формулу бинома Ньютона, можно убедиться, что сумма всех
n
вероятностей равна 1: ∑Cnm pmqn−m = (p + q)n =1.
m=0
Чтобы найти числовые характеристики с.в. X , введем новую с.в. Xi – индикатор события A ( i =1,2,...,n ). Она может принимать два значения: Xi =1, если в i-м испытании событие A произошло и Xi = 0 , если событие в
n
в i-м опыте не наступило. Исходная случайная величина X = ∑Xi . Ряд рас-
i=1
пределения с.в. Xi
42 |
|
|
|
|
|
|
Лекции 3-5 |
|
|
|
|
|
|
|
|
|
|
Xi |
|
0 |
1 |
|
|
|
|
p |
|
q |
p |
|
|
Математическое ожидание M (Xi )= p . |
|
|
|
||||
Дисперсия D (Xi )= M ((Xi )2 )−(M (Xi ))2 |
= p − p2 |
= pq . |
|||||
n |
|
|
|
|
|
|
|
Найдем характеристики X = ∑Xi , учитывая независимость величин Xi : |
|||||||
i=1 |
|
|
|
|
∑M (Xi )= np , |
||
M (X ) = M ∑Xi = |
|||||||
|
|
n |
|
n |
|
||
D (X ) = D ∑Xi |
i=1 |
|
i=1 |
σ (X ) = npq . |
|||
= ∑D |
(Xi |
) = npq , |
|||||
n |
|
n |
|
|
|
|
|
i=1 |
|
i=1 |
|
|
|
|
|
Найдем математическое ожидание и дисперсию относительной частоты по-
явления события A: |
m |
= |
|||||
|
|
|
|
|
|
n |
|
|
X |
|
1 |
M (X ) = |
|||
M |
|
|
= |
n |
|||
|
|||||||
|
n |
|
|
|
|
||
X
n
p ,
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
1 |
D (X ) = |
npq |
|
pq |
|
X |
|
pq |
|
||||
D |
|
|
= |
|
|
|
2 |
= |
|
, σ |
|
|
= |
|
. |
|
|
n |
2 |
n |
n |
|
n |
||||||||||
|
n |
|
|
|
|
|
|
n |
|
|
||||||
Полученный результат показывает обоснованность статистического опреде-
ления вероятности – среднее значение относительной частоты mn = p – веро-
ятности появления события в однократном испытании, а дисперсия, т. е., разброс значений вокруг среднего, уменьшается по мере роста n .
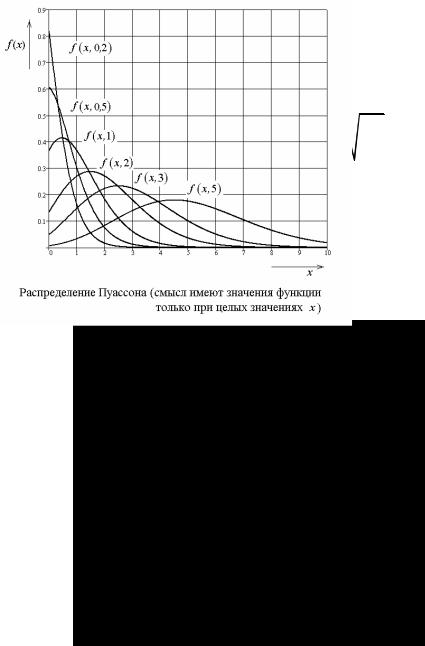
4.1.2. Распределение Пуассона
Случайная величина X, распределенная по закону Пуассона, принимает значения k = 0,1,2,... с вероятностями
P (X = k )= λk!k e−λ .
Число λ > 0 – параметр распределения, смысл которого будет уточнен при вычислении числовых характеристик распределения.
Легко убедиться, что сумма всех вероятностей
∞ |
|
|
|
|
|
|
∑P (X = k ) =1: |
|
|
|
|||
k =0 |
|
|
|
|
|
|
∞ |
|
k |
∞ |
|
k |
=e−λeλ =1. |
∑λ |
|
e−λ = e−λ ∑λ |
|
|||
k =0 |
k! |
k =0 |
k! |
|
||
