
ТВ_и_МС
.pdf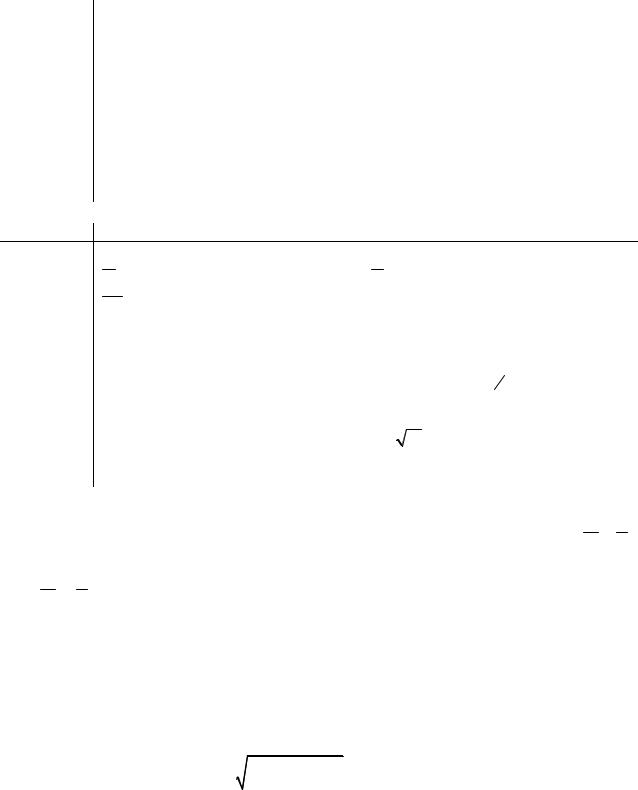
Проверка статистических гипотез |
123 |
Дальнейшее построение критической области для двух- и односторонней проверок проводится аналогично предыдущему, но вместо квантилей стандартного нормального распределения zα используются квантили распреде-
ления Стьюдента tα , определяемые по таблицам распределения Стьюдента,
а не Лапласа. Плотность распределения Стьюдента подобна функции Гаусса (плотности стандартного нормального распределения), но имеет отрицательный эксцесс, вследствие чего в «хвостах» распределения Стьюдента заключена бóльшая площадь. Следовательно, при том же уровне значимости значение tα будет больше, чем zα , т.е. доверительный интервал шире, чем по-
строенный на основе нормального распределения.
Пример:
Рассмотрим условия предыдущего примера ( H0 : средний размер детали X = 5,8 мм, альтернатива H1 : X ≠ 5,8 мм, выборочное среднее X B = 5,2 мм) с изменениями: выборка является малой, n =15 , выборочное среднеквадратическое отклонение s = 0,4 мм.
При том же уровне значимости α = 0,05 и числе степеней свободы ν = n −1 =15 −1 =14 найдем соответствующий квантиль tα 2 = 2,145 .
Допустимая область значений параметра t (−2,145;2,145). Вычисляя выбо-
рочное значение параметра tэксп |
= |
4,8 −5,2 |
14 = −3,74 < −2,145 видим, что в |
|
|
0,4 |
|
этом случае гипотеза H0 отклоняется. |
|
||
б) Сравнение средних значений двух совокупностей
Пусть имеются две совокупности, характеризующиеся средними X , Y и дисперсиями σx2 , σy2 . Выдвигается гипотеза, что эти средние равны, т.е.
H0 : X = Y . Для проверки этой гипотезы из каждой совокупности производится выборка: из первой – объемом n1 , в результате которой получаются
|
X |
B |
и s2 , из второй – объемом n , в результате которой получаются |
Y |
и s2 . |
|||||||||||||||||||||
|
|
x |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
B |
y |
|||||||||
|
sx2 и s2y – дисперсии выборок. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для проверки основной гипотезы используем критерий |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Θ = |
|
|
X B |
YB |
. |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
D ( |
|
|
− |
|
|
) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X B |
YB |
|
|
|
||||||||||
Так как M ( |
|
)= |
|
, M ( |
|
)= |
|
, при справедливости нулевой гипотезы H0 |
||||||||||||||||||
X B |
X |
YB |
Y |
|||||||||||||||||||||||
будем иметь M (Θ)= 0 . |
Используя свойства дисперсии и предполагая вы- |
|||||||||||||||||||||||||
борки (а следовательно, |
|
и выборочные средние) независимыми, |
получим |
|||||||||||||||||||||||
124 |
|
|
|
|
|
|
|
|
|
|
|
Лекции 11–12 |
|
|
|
|
|
|
|
|
2 |
σ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
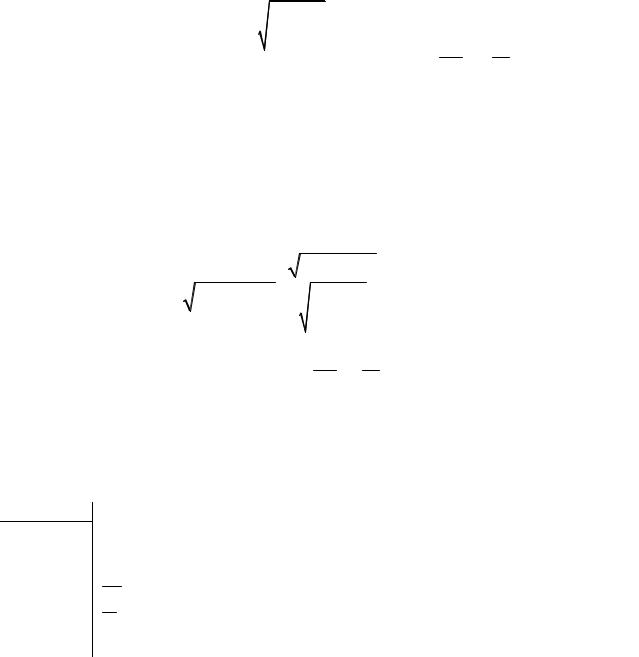
σ2 (X B −YB )=σ2 (X B )+σ2 (YB )= σnx + |
y |
. |
||||||||||
n |
||||||||||||
1 |
|
|
2 |
|
||||||||
Теперь сделаем дополнительное предположение, что дисперсии обеих совокупностей равны, т.е. σx2 =σy2 = σ2 . Это предположение нуждается в специ-
альной проверке, о чем речь пойдет в следующем разделе. Если принять это предположение, то
|
2 |
|
|
|
|
|
2 |
|
1 |
1 |
|
||
σ |
(X B −YB )=σ |
||||||||||||
|
|
|
|
+ |
|
. |
|||||||
|
|
n |
n |
||||||||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
||
Подставляя это выражение в формулу для критерия, получаем
Θ = |
|
X B |
− |
YB |
|
|
. |
|||
σ |
1 |
+ |
1 |
|
||||||
|
n |
n |
||||||||
|
|
|
|
|
||||||
|
|
|
1 |
|
|
2 |
|
|
||
Если обе выборки достаточно большого объема, то X B и YB распределены нормально, поэтому нормально будет распределен и критерий Θ. Заменяя
неизвестную дисперсию генеральной совокупности σ2 ее несмещенной выборочной оценкой
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑1 (xi − |
|
|
)2 + |
∑2 |
(yi − |
|
)2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
X B |
YB |
n s2 |
+ n s2 |
|
|
|
|
|||||||||||||||||||
s2 ≈ |
i=1 |
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
= |
|
1 x |
2 y |
, |
|
|
|
|||
|
|
|
n + n |
− 2 |
|
|
|
|
|
n + n − 2 |
|
|
|
||||||||||||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|||
придем к нормально распределенному критерию |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
− |
|
|
|
|
|
n1 + n2 − 2 |
|
|
|
|
|
|
|
||||||||
|
z = |
|
X |
B |
Y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
n1sx2 + n2 s2y |
|
|
1 1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
n |
+ n |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|||||
(число степеней свободы ν = n +n |
−2 , так как при расчете s2 |
и |
s2 |
исполь- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
зуются два соотношения для средних X B и YB .
Дальнейшая проверка ведется обычным образом с использованием таблиц функций распределения Лапласа. Если выборки малого объема и применение нормального распределения может привести к ошибкам, для того же критерия z используется распределение Стьюдента.
Пример:
Для проверки эффективности новой технологии отбираются две группы рабочих: в первой группе численностью n1 = 40 чел., где применяется новая
технология, получены следующие данные: средняя выработка в штуках X B = 84 , при этом sx =10,1, во второй группе численностью n2 = 54
YB = 77,5 sy = 8,4 .
Определим со значимостью α = 0,05 , действительно ли новая технология
Проверка статистических гипотез |
|
|
|
|
|
|
|
125 |
|
оказала влияние на производительность. |
|
|
|
|
|
|
|||
Вычисляем |
|
|
|
|
|
|
|
|
|
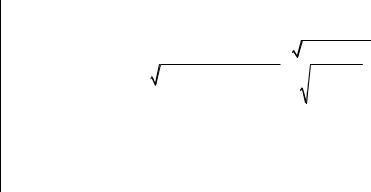
zэксп = |
|
84 −77,5 |
|
40 +54 −2 |
= 3,364 . |
||||
|
10,12 +54 8,42 |
|
1 |
|
1 |
|
|||
40 |
|
+ |
|
|
|||||
|
|
|
|
40 |
54 |
|
|
||
Критическое табличное значение критерия при α = 0,05 составляет 1,96. Так как zэксп >1,96 , то нулевая гипотеза об отсутствии влияния новой технологии должна быть отклонена. Если, считая n1 и n2 небольшими числами, воспользоваться распределением Стьюдента, получается тот же результат.
12.1.3. Сравнение дисперсий двух совокупностей
Проверять гипотезу о равенстве дисперсий двух совокупностей приходится во многих случаях: например, при анализе стабильности производства до и после введения технического новшества (стабильность выпуска продукции измеряется с помощью дисперсии измеряемого признака), при изучении качества измерительных приборов (сопоставление дисперсий показателей отдельных приборов), при изучении степени однородности двух совокупностей в отношении какого-либо признака (квалификации рабочих, успеваемости учащихся и т.д.). Необходимость проверки равенства дисперсий возникает, как было показано в предыдущем разделе, и при сравнении средних значений двух совокупностей, поскольку при этом в большинстве случаев предполагается, что генеральные дисперсии равны.
Пусть имеются две нормально распределенные совокупности, дисперсии которых равны σ12 и σ22 ; нулевая гипотеза H0 :σ12 =σ22 . Так как дисперсии генеральных совокупностей неизвестны, проверка гипотезы осуществляется на основе сопоставления выборочных дисперсий s12 и s22 . Если отношение s12 : s22 близко к 1, нет оснований отклонять нулевую гипотезу, если значи-
тельно отличается – гипотеза отклоняется. Для решения вопроса, насколько большим должно быть отличие выборочных дисперсий, чтобы отклонение нулевой гипотезы было достаточно обоснованным, используется отношение
F = |
s2 |
, где s |
2 |
> s |
2 |
. |
|
1 |
|
2 |
|||||
s2 |
|
||||||
|
|
1 |
|
|
|||
|
2 |
|
называющееся F –распределением |
||||
Распределение этого отношения, |
|||||||
Фишера – Снедекора, рассматривалось ранее, при обсуждении распределений, связанных с нормальным. Оно зависит от двух параметров – чисел степеней свободы числителя и знаменателя: ν1 = n1 −1 и ν2 = n2 −1, где n1 и n2 –
объемы выборок. Числа ν1 и ν2 указываются в фигурных скобках рядом с вычисленным значением F :
|
|
2 |
|
|
F = |
s1 |
; ν1 |
. |
|
|
||||
|
s |
2 |
ν |
|
|
|
2 |
2 |
|
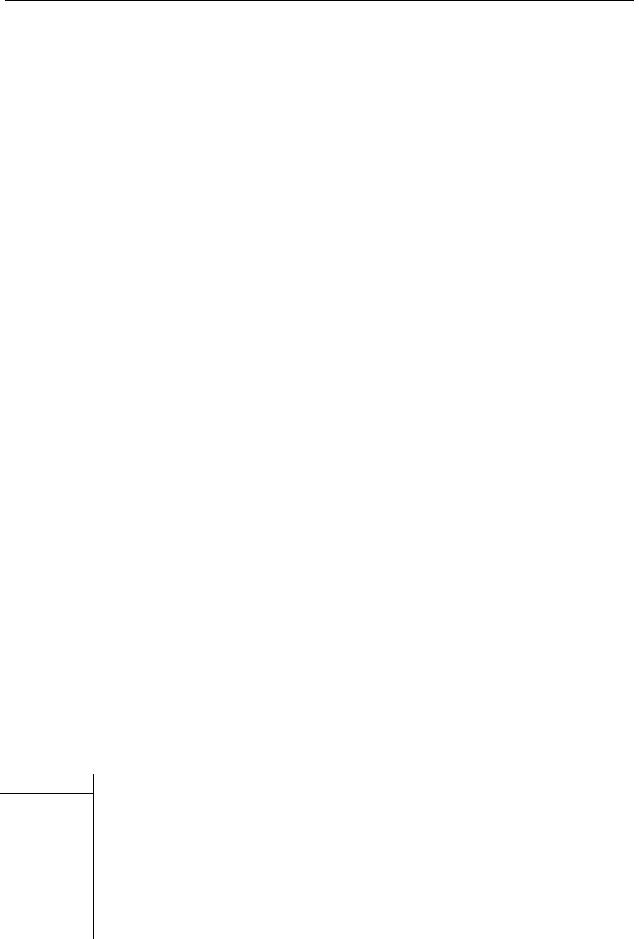
126 Лекции 11–12
Критическая область строится в зависимости от вида альтернативной гипотезы.
1). Нулевая гипотеза H0 :σ12 =σ22 . Альтернативная гипотеза H1 :σ12 >σ22 (считаем, что выборки пронумерованы так, что s12 > s22 ).
По заданному α и известным ν1 и ν2 по таблице распределения Фишера – Снедекора находим критическое значение Fα . Проверка гипотезы H0 сво-
дится к следующему правилу: если отношение выборочных дисперсий Fэксп > Fα , гипотеза H0 отклоняется; если Fэксп < Fα , гипотеза H0 не отклоняется.
2). Нулевая гипотеза H0 :σ12 =σ22 . Альтернативная гипотеза H1 :σ12 ≠σ22 .
В этом случае строим симметричную двустороннюю критическую область с
критическими точками F1 |
и F2 , определяемыми из неравенств |
|||
P (F < F )= α |
, |
P (F > F )= α . |
||
1 |
2 |
|
2 |
2 |
Правая критическая точка F2 |
находится непосредственно по таблице крити- |
|||
ческих точек распределения Фишера – Снедекора для уровня значимости α2
и степеней свободы ν1 и ν2 . Левых критических точек F1 таблица не содер-
жит, но, при выбранном симметричном способе построения критической области, достигается попадание критерия F в критическую область с вероятностью, равной уровню значимости α . Так как из определения уровня значи-
мости P (F < F1 )+ P (F > F1 )=α , то выбирая P (F > F2 )= α2 , мы одновре-
менно достигаем и P (F < F1 )= α2 . Проверка гипотезы H0 производится по тому же правилу, что и в случае односторонней критической области, но таб-
личные значения критерия ищутся для значения α |
, вдвое меньшего, чем за- |
|
2 |
|
|
данный уровень значимости: если отношение |
выборочных |
дисперсий |
Fэксп > F2 , гипотеза H0 отклоняется; если Fэксп < F2 , гипотеза H0 |
не отклоня- |
|
ется. |
|
|
Пример:
Два завода производят однотипные измерительные приборы. Для сравнения качества продукции проведены серии измерений приборами каждого завода. Из совокупностей наблюдений сделаны выборки, объемы которых
n1 = n2 =15 , исправленные выборочные дисперсии s12 =1,35 и s22 = 0,45 . При уровне значимости α = 0,1 проверить гипотезу о равенстве генеральных дисперсий при альтернативной гипотезе σ12 ≠σ22 .
Найдем наблюдаемое значение критерия

Проверка статистических гипотез |
|
|
|
|
127 |
F |
= 1,35 = 3 . |
|
|
|
|
эксп |
0,45 |
|
|
|
|
|
|
|
|
|
|
Ищем табличное значение критерия при уровне значимости, вдвое меньше |
|||||
заданного, т.е. при α = 0,05 |
для степеней свободы ν |
1 |
=ν |
2 |
= n −1 =14 : |
2 |
|
|
1 |
||
|
|
|
|
|
|
Fкрит = 2,48 . Так как Fэксп > Fкрит , нулевая гипотеза о равенстве дисперсий не |
|||||
принимается, различие дисперсий статистически значимо. Приборы второго завода производят измерения с меньшей дисперсией, с меньшим разбросом и поэтому более предпочтительны.
12.1.4.Сравнение исправленной выборочной дисперсии
сгипотетической генеральной дисперсией
нормальной совокупности
Пусть генеральная совокупность распределена нормально и есть основания предполагать (скажем, на основании предыдущих испытаний), что гипотети-
ческая (предполагаемая) дисперсия генеральной совокупности равна σ02 . Из генеральной совокупности извлечена выборка объема n и по ней вычислена исправленная выборочная дисперсия s2 с ν = n −1 степенями свободы.
Требуется проверить, значимо ли отличие s2 от σ02 . Как нулевую гипотезу выдвигаем H0 :σ2 =σ02 . На практике рассматриваемая гипотеза проверяется,
если нужно проверить точность приборов, инструментов, станков, устойчивость технологических процессов. Например, известна допустимая мера рас-
сеяния размера деталей σ02 , изготовляемых станком-автоматом, и по найденной по выборке характеристике рассеяния s2 требуется определить, значимо ли отличие s2 от σ02 , нужна переналадка станка или не нужна.
В качестве критерия проверки нулевой гипотезы примем случайную величи-
(n −1)s2
ну . Можно доказать, что она распределена (при нормальном рас-
σ02
пределении признака) по закону χ2 с ν = n −1 степенями свободы. Итак, критерий проверки нулевой гипотезы
χ2 = (n −1)s2 .
σ02
Критическая область строится в зависимости от вида альтернативной гипотезы.
1). Нулевая гипотеза H0 :σ2 =σ02 . Альтернативная гипотеза H1 :σ2 >σ02 . В этом случае строим правостороннюю критическую область из усло-
вия
P (χ2 > χкрит2 )= α .
128 |
|
|
|
|
|
Лекции 11–12 |
По таблице распределения χ2 |
находим значение χкрит2 , и, сравнивая |
|||||
χэксп2 с χкрит2 |
, при χэксп2 |
> χкрит2 |
отклоняем нулевую гипотезу, при χэксп2 < χкрит2 |
|||
принимаем нулевую гипотезу. |
|
|
|
|
||
2). Нулевая |
гипотеза |
H0 :σ2 |
=σ02 . |
Альтернативная |
гипотеза H1 :σ2 ≠σ02 . |
|
В этом случае строим симметричную двустороннюю критическую об- |
||||||
ласть из условий |
|
.лев )= α |
|
|
.прав )= α . |
|
|
P (χ2 |
< χкрит2 |
, P (χ2 |
> χкрит2 |
||
|
|
|
2 |
|
|
2 |
В таблице критических точек распределения χ2 |
приводятся только «правые» |
|||||
критические точки. Это затруднение можно обойти следующим образом: так
как события χ2 < χкрит2 |
.лев |
и χ2 ≥ χкрит2 |
.лев несовместны и в сумме составляют |
|||||||||
все пространство событий, то |
|
|
|
|
|
|
||||||
|
|
|
|
|
P (χ2 < χкрит2 |
.лев )+ P (χ2 ≥ χкрит2 |
.лев )=1. |
|||||
Поэтому P (χ2 < χкрит2 |
.лев ) |
находим из условия P (χ2 ≥ χкрит2 |
.лев )=1− α . |
|||||||||
При χэксп2 |
< χкрит2 |
|
|
|
χ2 > χкрит2 |
|
|
|
|
|
2 |
|
.лев или |
.прав |
нулевая гипотеза отклоняется, в про- |
||||||||||
тивном случае – принимается. |
|
|
|
|
|
|
||||||
3). Нулевая гипотеза |
H0 :σ2 =σ02 . |
Альтернативная |
гипотеза H1 :σ2 < σ02 . |
|||||||||
Левосторонняя критическая область строится из условия |
|
|||||||||||
|
|
|
|
|
|
P (χ2 ≥ χкрит2 |
)=1−α . |
|
|
|||
При χэксп2 |
< χкрит2 |
.лев нулевая гипотеза отклоняется, в противном случае – при- |
||||||||||
нимается.
12.2.Непараметрические гипотезы. Критерии согласия Пирсона и Колмогорова
Впредыдущих параграфах рассматривались методы проверки гипотез относительно отдельных параметров генерального распределения. Особое место занимают гипотезы относительно согласованности выборочного распределения с теоретическим (генеральным) распределением. Критерии согласия позволяют ответить на вопрос о том, являются ли различия между выборочным и теоретическим распределениями столь незначительными, что они могут быть приписаны влиянию случайных факторов, или нет.
Пусть закон распределения генеральной совокупности неизвестен, но есть основания предполагать, что он имеет определенный вид. В частности, если выполняются условия центральной предельной теоремы, есть основания ожидать, что генеральное распределение – нормальное; если выборочное среднее и выборочная дисперсия равны, то можно предполагать, что генеральная совокупность распределена по закону Пуассона и т.д. Эти утвержде-

Проверка статистических гипотез |
129 |
ния носят характер гипотез, а не категорических утверждений, и должны быть подвергнуты статистической проверке.
Для проверки гипотезы H0 : закон распределения имеет данный вид (на-
пример, равномерный, нормальный и др.) используется специально подобранная с. в., которая называется критерием согласия.
Критерий согласия есть критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Имеется несколько критериев согласия: χ2 (хиквадрат) Пирсона, Колмогорова, Мизеса – Смирнова и др.. Мы познакомимся с критериями χ2 и Колмогорова.
12.2.1. Критерий Пирсона
Рассмотрим случай, когда выборка представляется интервальным статистическим рядом. Для изучения случайной величины Х проведено n опытов, диапазон наблюдавшихся значений величины Х разбит на q интервалов. Ряд распределения имеет вид:
|
Интервалы |
(x1 ...x2 ) |
(x2 ...x3 ) |
… |
(xq ...xq+1 ) |
|
||
|
|
|
|
|
|
|
|
|
|
pi = |
mi |
|
p1 |
p2 |
… |
pq |
|
|
n |
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
q |
|
где mi – количество экспериментальных данных в i -м интервале, ∑mi = n . |
||||||||
|
|
|
|
|
|
|
i=1 |
|
В соответствии с предполагаемым теоретическим законом распределения, вычислим вероятности попадания с.в. в соответствующий интервал pi = P(xi < X < xi +1 ) и рассмотрим величину
q |
|
χ2 = ∑ n (pi − pi )2 , |
|
i=1 |
pi |
которая характеризует степень расхождения теоретических и эмпирических данных. Учитывая, что pi = mni , получим
q |
(mi |
−npi )2 |
χнабл2 = ∑ |
|
. |
i=1 |
|
npi |
Можно показать, что при n → ∞ распределение этой с.в., независимо от того, каков закон распределения генеральной совокупности, стремится к рас-
пределению Пирсона χ2 с числом степеней свободы ν = q −1−k , где k –
число параметров генерального распределения, оцениваемых на основании наблюденных данных. Если проверяется согласие выборочного распределения с распределение Пуассона, единственный параметр которого оценивается по выборочным данным, то ν = q −2 , если проверяется согласие с нор-

130 Лекции 11–12
мальным распределением, для которого по выборочным данным оцениваются два параметра X и σ , то ν = q −3 и т.д.
При полном совпадении теоретического и экспериментального распределений χ2 = 0 , в противном случае χ2 > 0 . Задавшись уровнем значимости α , находим табличное критическое значение χα2 , при χнабл2 < χα2 принимаем гипотезу H0 , при χнабл2 ≥ χα2 отклоняем гипотезу H0 о виде распределения.
В связи с асимптотическим характером закона Пирсона χ2 должны выполняться следующие условия:
1)выборка должна образовываться в результате случайного отбора;
2)объем выборки n должен быть достаточно большим (практически не менее 50 единиц);
3)численность каждой группы должна быть не менее 5 (если это условие не выполняется, производится объединение малочисленных интервалов).
Пример:
На экзамене экзаменатор задает студенту только один вопрос по одной из четырех частей курса. Из 100 студентов 26 получили вопрос по первой части, 32 - по второй, 17 - по третьей, остальные - по четвертой. При уровне значимости α=0,05 проверить гипотезу, что вероятность получить вопрос по любой из четырех частей для пришедшего на экзамен одинакова.
Объемы выборки и групп n =100 , m1 = 26 , m2 = 32 , m3 =17 , m4 =100 −(26 +32 +17)= 25 . Вероятность получить вопрос по любой из че-
тырех частей одинакова, т.е. pi = p = 0,25 , |
npi = 25; |
(i =1,2,3,4). |
|||||||||
Наблюдаемое значение критерия |
|
|
|
|
|
|
|
||||
χ2 |
= |
(26 −25)2 |
+ |
(32 −25)2 |
+ |
(17 −25)2 |
+ |
(25 −25)2 |
= |
||
|
|
|
|
|
|
||||||
набл |
|
25 |
|
25 |
|
|
|
25 |
|
25 |
|
|
|
|
|
|
|
|
|
||||
|
|
= |
1+ 49 +64 |
= |
114 |
= 4,56 . |
|
|
|
||
|
|
|
|
25 |
|
25 |
|
|
|
|
|
Так как ни один из параметров предполагаемого распределения не находился по выборке, то k = 0 б q = 4 и число степеней свободы
ν = 4 −(1+0)= 3 . По таблице для ν = 3 и α=0,05 находим критическую
точку χкр2 = 7,82 . Так как χнабл2 = 4,56 < χкр2 = 7,82 , гипотеза о равновероятности получить вопрос по любой из четырех частей курса не отвергается.
Пример:
Распределение признака Х в выборке задано интервальным вариационным рядом (первый и второй столбцы таблицы).
При уровне значимости α=0,05 проверить гипотезу о нормальном распределении Х в генеральной совокупности.
|
* |
|
* |
|
* |
−mi ) |
2 |
|
(m*i −mi )2 |
|
xi |
mi |
mi = n∆Ф |
mi |
−mi |
(mi |
|
|
|
|
|
|
|
mi |
|
|||||||
|
|
|
|
|
|
|
|
|
|

Проверка статистических гипотез |
|
|
|
|
|
|
|
131 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9,0 – 9,1 |
|
|
|
|
|
|
|
|
-0,8 |
0,64 |
0,08 |
|
2 |
|
1,4 |
|||||||||||
|
9,1 – 9,2 |
|
5 |
|
|
6,4 |
|
|
|
|
|
||
|
9,2 – 9,3 |
|
27 |
|
|
23,2 |
|
3,8 |
14,4 |
0,62 |
|
||
|
9,3– 9,4 |
52 |
62,0 |
-10 |
100 |
1,61 |
|
||||||
|
9,4 – 9,5 |
117 |
126 |
-9 |
81 |
0,64 |
|
||||||
|
9,5 – 9,6 |
203 |
189 |
4 |
16 |
0,08 |
|
||||||
|
9,6 – 9,7 |
228 |
214,2 |
13,8 |
190,4 |
0,89 |
|
||||||
|
9,7 – 9,8 |
180 |
181,3 |
1,3 |
1,7 |
0,01 |
|
||||||
|
9,8 – 9,9 |
105 |
115,7 |
10,7 |
174,5 |
0,99 |
|
||||||
|
9,9 – 10,0 |
60 |
54,7 |
5,3 |
28,1 |
0,51 |
|
||||||
|
10,0 – |
14 |
19,5 |
5,5 |
30,3 |
1,55 |
|
||||||
|
10,1 |
|
4 |
|
|
5,2 |
|
|
|
|
|
||
|
10,1 – |
|
|
|
|
|
|
|
|
0,7 |
0,49 |
0,08 |
|
|
2 |
|
|
1,1 |
|
||||||||
|
10,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
||
|
10,2 – |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10,3 – |
|
|
|
|
|
|
|
|
|
|
|
|
|
10,4 |
|
|
|
|
|
|
|
|
|
– |
|
|
|
Итого: |
1000 |
999,7 |
– |
7,06 |
|
|||||||
По данному интервальному ряду составим вспомогательный ряд (в качестве значений возьмем середины интервалов, в качестве вероятностей – относительные частоты):
X |
9,05 |
9,15 |
9,25 |
9,35 |
9,45 |
9,55 |
9,65 |
|
|
|
|
|
|
|
|
|
|
w |
0,002 |
0,005 |
0,027 |
0,052 |
0,117 |
0,203 |
0,228 |
|
|
|
|
|
|
|
|
|
|
X |
9,75 |
9,85 |
9,95 |
10,05 |
10,15 |
10,25 |
10,35 |
|
|
|
|
|
|
|
|
|
|
w |
0,180 |
0,105 |
0,060 |
0,014 |
0,004 |
0,002 |
0,001 |
|
|
|
|
|
|
|
|
|
|
Для вспомогательного ряда найдем выборочное среднее X B = 9,643 и исправленную выборочную дисперсию sB2 = 0,166 . Принимая их в качестве то-
чечных оценок соответствующих параметров генерального распределения, по таблице значений функции Лапласа найдем теоретические частоты (третий столбец исходной таблицы).
При дальнейших вычислениях объединим интервалы с малыми числами наблюдений (числа в таблице обведены рамками) и найдем наблюдаемое зна-
чение критерия χнабл2 = 7,06 (четвертый – шестой столбцы исходной таблицы). При уровне значимости α=0,05 и числе степеней свободы ν =11−(1+ 2)= 8 табличное критическое значение χкр2 =15,5 .
Так как χнабл2 = 7,06 < χкр2 = 15,5 , гипотеза о нормальном законе распределения Х в генеральной совокупности не противоречит опытным данным (гипотеза не отвергается).

132 |
Лекции 11–12 |
12.2.2. Критерий Колмогорова
Величина χ2 зависит от группировки выборочной совокупности по интервалам, что вносит в оценку дополнительный элемент случайности.
В ряде случаев оказывается удобнее пользоваться критерием Колмогорова, основанном на сравнении эмпирической функции распределения F* (x)
(построенной на основании опытных данных) и предполагаемой теоретической функции распределения F (x). В качестве меры расхождения берется
максимум абсолютной величины разности между опытной F* (x) и теоретической F (x) функциями распределения накопленных относительных частот,
D = max |
|
∆ |
n |
|
= max |
|
F* (x)− F (x) |
|
. |
|
|
|
|
|
|||||||
|
|
|||||||||
n |
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Очевидно, если расхождения слишком велики, то гипотеза о том, что функция распределения генеральной совокупности имеет вид F (x), отвергается.
При достаточно больших объемах выборки (как показывает практика, при n > 20 ) можно пользоваться предельным распределением критерия, предложенным А.Н. Колмогоровым, формально справедливым при n → ∞: если функция распределения генеральной совокупности F (x) непрерывна, то при n → ∞
|
∞ |
при t > 0; |
P(Dn |
∑(−1)k e−2k 2t2 , |
|
n < t ) n→∞→K (t )= k =−∞ |
|
|
|
|
при t ≤ 0. |
|
0, |
При заданном уровне значимости α критерий Колмогорова отклоняет основную гипотезу H0 о виде функции распределения F (x), если Dn > D1−α ,
где D1−α – квантиль уровня 1−α распределения случайной величины D при
условии истинности основной гипотезы |
H0 . Если Dn ≤ D1−α , то статистиче- |
|||||
ские данные не противоречат гипотезе H0 . Квантиль D1−α находится из урав- |
||||||
нения |
|
|
|
t1−α |
|
|
K (t |
)=1−α , |
D |
= |
. |
||
|
||||||
1−α |
|
1−α |
|
n |
||
|
|
|
|
|||
