ТВ_и_МС
.pdfОГЛАВЛЕНИЕ |
|
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ВЕРОЯТНОСТЕЙ |
|
Лекции 1 – 2. СЛУЧАЙНЫЕ СОБЫТИЯ ............................................................... |
7 |
1.1. Введение...................................................................................................... |
7 |
1.2. Основные понятия...................................................................................... |
8 |
1.3. Вероятность. Варианты определения....................................................... |
10 |
1.3.1. Относительная частота события, статистическое определение ве- |
|
роятности............................................................................................. |
10 |
1.3.2. Классическое определение вероятности........................................... |
11 |
1.3.2.1. Основные формулы комбинаторики........................................ |
11 |
Выборки без возвращения ....................................................... |
12 |
Выборки с возвращением......................................................... |
13 |
1.3.3. Геометрическое определение вероятности ........................................ |
14 |
1.3.4. Аксиоматическое определение вероятности...................................... |
15 |
2.1. Теорема сложения вероятностей.............................................................. |
16 |
2.2. Условная вероятность события. Теорема умножения вероятностей.... |
16 |
2.3. Вероятность появления хотя бы одного события................................... |
18 |
2.4. Формула полной вероятности................................................................... |
19 |
2.5. Формула Бейеса (теорема гипотез) .......................................................... |
20 |
2.6. Повторение опытов. Формула Бернулли................................................. |
22 |
2.7. Предельные случаи формулы Бернулли.................................................. |
24 |
2.7.1. Локальная предельная теорема Муавра-Лапласа ............................ |
24 |
2.7.2. Интегральная предельная теорема МуавраЛапласа...................... |
24 |
2.7.3. Формула Пуассона.............................................................................. |
25 |
Лекции 3 – 5. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ............................................................ |
27 |
3.1. Случайные величины. Виды случайных величин. |
|
Закон распределения случайной величины................................................ |
27 |
3.1.1. Биномиальное распределение. Распределение Пуассона. |
|
Поток событий..................................................................................... |
29 |
3.2. Функция распределения случайной величины ....................................... |
30 |
3.3. Непрерывная случайная величина. Плотность распределения............. |
32 |
3.4. Числовые характеристики случайных величин...................................... |
34 |
3.4.1. Математическое ожидание................................................................. |
34 |
3.4.2. Дисперсия. Среднее квадратическое отклонение............................ |
35 |
3.4.3. Мода, медиана, квантили ................................................................... |
36 |
3.4.4. Моменты случайных величин............................................................ |
37 |
4.1. Основные законы распределения непрерывных случайных величин |
|
и их числовые характеристики.................................................................... |
41 |
4.1.1. Биномиальное распределение............................................................ |
41 |
3
4.1.2. Распределение Пуассона.................................................................... |
42 |
4.1.3. Равномерное распределение .............................................................. |
43 |
4.1.4. Показательное распределение ........................................................... |
45 |
4.1.5. Нормальное распределение (распределение Гаусса) ...................... |
46 |
5.1. Функции от случайной величины............................................................. |
48 |
5.2. Числовые характеристики функции случайной величины.................... |
51 |
5.3. Распределения, связанные с нормальным............................................... |
52 |
5.3.1. Распределение χ2 (Пирсона)............................................................. |
52 |
5.3.2. t – распределение Стьюдента............................................................ |
53 |
5.3.3. F – распределение Фишера – Снедекора.......................................... |
54 |
Лекция 6. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.................................. |
55 |
6.1. Многомерные случайные величины ........................................................ |
55 |
6.1.1. Функция распределения многомерной случайной величины........ |
56 |
6.1.2. Дискретные многомерные случайные величины (ДМСВ) ............. |
57 |
6.1.3. Непрерывные многомерные случайные величины (НМСВ) .......... |
59 |
6.2. Зависимые и независимые случайные величины.................................... |
60 |
6.2.1. Условные законы распределения...................................................... |
61 |
6.3. Числовые характеристики двумерной случайной величины................. |
63 |
6.3.1. Корреляционный момент и коэффициент корреляции................... |
64 |
6.3.2. Числовые характеристики условных распределений...................... |
67 |
6.3.3. Линейная регрессия. Прямые линии среднеквадратической |
|
регрессии.............................................................................................. |
68 |
6.3.4. Линейная корреляция. Двумерный нормальный закон |
|
распределения...................................................................................... |
70 |
Лекция 7. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ................... |
72 |
7.1. Закон больших чисел (предельные теоремы теории вероятностей)..... |
72 |
7.1.1. Неравенство Чебышева....................................................................... |
73 |
7.1.2. Теорема Чебышева.............................................................................. |
75 |
7.1.3. Теорема Маркова................................................................................. |
76 |
7.1.4. Теорема Бернулли............................................................................... |
77 |
7.2. Центральная предельная теорема............................................................. |
78 |
7.2.1. Формула Муавра-Лапласа как частный случай .............................. |
|
центральной предельной теоремы .................................................... |
79 |
4
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ |
|
Лекции 8 - 10. ВЫБОРКИ. СТАТИСТИЧЕСКИЕ ОЦЕНКИ |
|
ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ............................................ |
82 |
8.1. Задачи математической статистики ......................................................... |
82 |
8.2. Генеральная и выборочная совокупности. Способы отбора................. |
83 |
8.3. Статистическое распределение выборки................................................. |
85 |
8.4. Полигон и гистограмма............................................................................. |
87 |
8.5. Эмпирическая функция распределения................................................... |
88 |
8.6. Числовые характеристики статистического распределения выборки.. |
90 |
8.7. Числовые характеристики генеральной совокупности.......................... |
92 |
9.1. Статистические оценки параметров распределения............................... |
93 |
9.2. Точечные и интервальные оценки. Доверительный интервал, |
|
точность оценки, доверительная вероятность (надежность).................. |
94 |
9.3. Несмещенные, эффективные и состоятельные оценки.......................... |
96 |
9.4. Точечная оценка генерального среднего |
|
по выборочному среднему......................................................................... |
96 |
9.5. Точечная оценка генеральной дисперсии |
|
по исправленной выборочной дисперсии............................................... |
97 |
9.6. Метод моментов для точечной оценки параметров распределения..... |
98 |
9.7. Метод максимального правдоподобия для точечной оценки |
|
параметров распределения..................................................................... |
100 |
10.1. Интервальные оценки............................................................................ |
103 |
10.2. Интервальная оценка математического ожидания нормально |
|
распределенной случайной величины при известном σ. .................... |
104 |
10.3. Интервальная оценка математического ожидания нормально |
|
распределенной случайной величины при неизвестном σ. ................ |
106 |
10.4. Интервальная оценка среднего квадратического отклонения σ нор- |
|
мального распределения......................................................................... |
108 |
Лекции 11 - 12. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ ......................... |
111 |
11.1. Статистическая гипотеза. Параметрическая и непараметрическая, |
|
нулевая и конкурирующая, простая и сложная гипотезы................... |
111 |
11.2. Ошибки первого и второго рода........................................................... |
112 |
11.3. Статистический критерий. Критическая область. |
|
Область принятия гипотезы. Критические точки................................ |
113 |
11.4. Уровень значимости и мощность критерия......................................... |
114 |
11.5. Виды критических областей ................................................................. |
115 |
11.6. Методика проверки гипотез.................................................................. |
115 |
12.1. Некоторые типичные задачи проверки параметрических гипотез... |
117 |
12.1.1 Проверка гипотез о доле признака................................................. |
117 |
5
12.1.2 Проверка гипотез о среднем значении........................................... |
121 |
12.1.3 Сравнение дисперсий двух совокупностей................................... |
125 |
12.1.4 Сравнение исправленной выборочной дисперсии с гипотетичес- |
|
кой генеральной дисперсией нормальной совокупности............. |
127 |
12.2. Непараметрические гипотезы. Критерии согласия |
|
Пирсона и Колмогорова......................................................................... |
128 |
12.2.1 Критерий Пирсона ........................................................................... |
129 |
12.2.2. Критерий Колмогорова................................................................... |
132 |
Лекции 13-14. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ. |
|
КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ........... |
134 |
13. Основы корреляционного анализа................................................................. |
134 |
13.1. Основные понятия.................................................................................. |
134 |
13.2. Элементы теории корреляции. Анализ парных связей...................... |
136 |
13.3. Оценка показателя связи по выборочным данным. |
|
Корреляционное поле............................................................................. |
139 |
13.4. Анализ коэффициента корреляции....................................................... |
140 |
13.4.1. Точечная оценка коэффициента корреляции............................... |
140 |
13.4.2. Интервальная оценка коэффициента корреляции |
|
и проверка значимости..................................................................... |
142 |
14. Основы регрессионного анализа.................................................................... |
144 |
14.1. Условные средние. Выборочные уравнения регрессии..................... |
144 |
14.2. Корреляционная таблица. Выборочные линии регрессии................. |
145 |
14.3. Линейная регрессия. Выборочный коэффициент корреляции.......... |
149 |
Лекции 15-16. ОСНОВЫ ДИСПЕРСИОННОГО АНАЛИЗА............................. |
151 |
15.1. Исходные понятия.................................................................................. |
151 |
15.2. Групповое и общее среднее. Групповая, внутригрупповая, |
|
межгрупповая и общая дисперсии ........................................................ |
152 |
15.3. Однофакторный анализ при полностью случайном плане |
|
эксперимента ........................................................................................... |
155 |
16.1. Однофакторный анализ при группировке по случайным блокам..... |
159 |
16.2. Двухфакторный анализ при полностью случайном |
|
плане эксперимента................................................................................. |
162 |
ПРИЛОЖЕНИЯ....................................................................................................... |
167 |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.................................................................... |
186 |
6
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Лекции 1–2 СЛУЧАЙНЫЕ СОБЫТИЯ
В лекциях рассматриваются основные понятия теории вероятностей: вероятность и случайные события. Приведены различные варианты определений вероятности, отражающие историческое развитие теории вероятностей, изложены основные теоремы, применяемые при построении математических моделей случайных событий.
1.1.Введение
1.2.Основные понятия
1.3.Вероятность. Варианты определения
1.3.1.Относительная частота события, статистическое определение вероятности
1.3.2.Классическое определение вероятности
1.3.3.Геометрическое определение вероятности
1.3.4.Аксиоматическое определение вероятности
2.1.Теорема сложения вероятностей
2.2.Условная вероятность события. Теорема умножения вероятностей
2.3.Вероятность появления хотя бы одного события
2.4.Формула полной вероятности
2.5.Формула Бейеса (теорема гипотез)
2.6.Повторение опытов. Формула Бернулли
2.7.Предельные случаи формулы Бернулли
2.7.1.Локальная предельная теорема Муавра-Лапласа
2.7.2.Интегральная предельная теорема Муавра-Лапласа
2.7.3.Формула Пуассона
1.1.Введение
Наблюдаемые события можно разделить на три группы: достоверные, невозможные, неопределенные. При создании определенных условий достоверные события обязательно происходят, невозможные – обязательно не происходят, неопределенные – могут и произойти, и не произойти. Скажем, при подбрасывании монеты событие «монета упадет» – достоверное, событие «монета останется висеть в воздухе» – невозможное, событие «монета упадет гербом вверх» – неопределенное или случайное. Теорией вероятностей называется наука, изучающая закономерности в случайных явлениях.
Для того чтобы к неопределенному событию могли быть применены методы теории вероятностей, необходима возможность многократного наблюдения события при повторении комплекса условий. В рамках теории вероят-
8 |
Лекции 1-2 |
ностей термин случайное явление (событие) относится к именно таким со-
бытиям, которые могут наблюдаться многократно. С этой точки события
«матч выиграет команда А» или «Паша женится на Маше» – неопределенные, но не случайные в смысле, вкладываемом в это понятие в теории вероятностей: они не могут повториться при точно таких же условиях, при повторной встрече игроки будут в иной физической форме, молодые люди будут обладать иным опытом и т.п.
Элементы случайности присутствуют во всех явлениях природы. На практике случайными элементами можно пренебречь, рассматривая вместо реального явления его модель. Это схема точных наук: от условий опыта к его однозначному результату. Есть задачи, для которых эта схема плоха. Это задачи, где результат опыта существенно зависит от большого числа факторов, которые учесть невозможно.
1.2. Основные понятия
Пусть проводится некоторый опыт (как синонимы используются названия эксперимент, наблюдение, испытание), исход которого предсказать заранее нельзя.
ОСлучайным событием (событием, исходом) называется любой исход опыта, который может произойти или не произойти. События обычно обозначаются заглавными латинскими буквами.
Пример:
Опыт – бросание монеты; событие А – появление герба.
ОЭлементарным исходом (элементарным событием) называют любой простейший (неделимый в условиях данного опыта) исход опыта. Элементарные исходы должны удовлетворять следующим условиям:
–в результате опыта один из исходов обязательно происходит;
–появление одного из элементарных исходов исключает появление остальных;
–в рамках данного опыта нельзя разделить элементарный исход на более мелкие составляющие.
Пример:
При бросании игральной кости возможно появление 1, 2, 3, 4, 5, 6 очков, при этом появление 4 очков – событие элементарное, появление четного количества очков – событие не элементарное, оно составляется из 3 элементарных: появление 2, ,4 или 6 очков.
ОМножество всех элементарных событий (исходов), связанных с данным опытом, называют пространством элементарных событий Ω, которое отождествляется с достоверным событием. Элементарные исходы ωi Ω
– элементы этого множества.
Случайные события |
9 |
!Так как в дальнейшем события будут рассматриваться как некоторые множества, составленные из «более простых» событий, напомним основные операции над множествами.
ОМножеством называется любая совокупность объектов произвольной природы, каждый их которых называется элементом множества. В дальнейшем множества (и события) будем обозначать большими латин-
скими буквами, элементы – малыми латинскими, a A – «элемент a принадлежит множеству A ».
!В дальнейшем операции над событиями (и над множествами) будем иллюстрировать диаграммами Эйлера – Венна. В них пространство исходов изображается на плоскости в виде прямоугольника, элементарные события – точками внутри прямоугольника, более сложные события – подмножествами точек прямоугольника.
О
О
Пустым множеством называется множество, не содержащее ни одного элемента (обозначается Ø). Пустое множество соответствует невозможному событию, т.е. такому, которое в данном опыте вообще не может произойти.
Множество В называется подмножеством множества А, если все элементы В содержатся в А. Обозначение B A .
ОПересечением (произведением) множеств А и В на-
зывается множество D = A∩ B ( D = A×B , D = AB ), состоящее из элементов, входящих одновременно и в
А, и в В.
ОСобытия А и В называются несовместными (непересекающимися), если они не могут появиться вме-
сте (их пересечение является невозможным событи-
ем, AB = ).
ООбъединением (суммой) множеств А и В называется множество C = A B (C = A + B ), состоящее из всех элементов, входящих хотя бы в одно из множеств А или В. (А и В см. на первом рисунке)
ОРазностью множеств А и В называется множество
F = A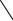
B ( F = A − B ), состоящее из элементов, входящих в А, и не входящих в В.
О Противоположным событиюA называется событиеA , происходящее тогда и только тогда, когда не происходит событие A . Используется также термин дополнение события A : A = Ω − A .
10 |
Лекции 1-2 |
О |
События A1 , A2 ,...An образуют полную группу событий, если: |
|
1) Ai Aj = , i ≠ j , 2) A1 + A2 +...+ An = Ω. |
Пример:
Пространство элементарных событий Ω. Выпадение герба и выпадение решки при бросании монеты.
1.3. Вероятность. Варианты определения
ОПоявление события А обладает какой-то степенью возможности, которую можно измерить численно. Это число называется вероятностью события.
ОВероятность достоверного события, т.е. такого, которое в результате опыта неизбежно должно произойти, равна 1.
ОВероятность невозможного события, т.е. такого, которое в данном опы-
те вообще не может произойти, равна 0.
!Все события, возможные, но не достоверные, будут иметь вероятность между 0 и 1.
Пример:
Выпадение герба и выпадение решки при бросании монеты.
1.3.1. Относительная частота события, статистическое определение вероятности
Пусть проведена серия из n испытаний при одних и тех же условиях; при этом фиксируется появление события А и событие А произошло m раз.
О Число m называют частотой наступления события А. Ясно, что
0 ≤ m ≤ n .
ООтносительной частотой W (A) события А называют отношение числа
испытаний, в которых событие А появилось, к числу всех проведенных испытаний: W (A) = mn .
Если проводить серии опытов с большим числом испытаний при одинаковых условиях, то во многих случаях относительная частота наблюдаемого события будет мало меняться от серии к серии. Этот факт (статистическая устойчивость) проверен многократно в различных экспериментах.
ОЧисло, около которого группируются относительные частоты при увеличении числа испытаний, называется статистической вероятностью рас-
сматриваемого события.
Обозначение вероятности события А: P (A).
И относительная частота, и статистическая вероятность обладают следующими свойствами:
Случайные события |
11 |
1.0 ≤ P (A)≤1, т.к. P (A) = mn , и m ≥ 0,n > 0 , m ≤ n .
2.P (Ω) =1, т.к. m = n .
3.P ( ) = 0 , т.к. n0 = 0 .
4.P (A + B) = P (A)+ P (B), если AB = (события несовместны).
Основной недостаток статистического определения вероятности состоит в необходимости проведения большого числа опытов для вычисления вероятности в соответствии с этим определением.
1.3.2. Классическое определение вероятности
ОСобытие называется благоприятствующим событию A , если появление этого события влечет за собой появление события A .
ОПусть пространство элементарных событий Ω:
1)состоит из конечного числа элементарных исходов;
2)элементарные исходы w1 , w2 ,..., wn равновозможны (нет оснований счи-
тать, что одни происходят чаще, чем другие).
!Такая модель называется классической схемой. Эта схема применима к бросанию игральной кости: из симметрии кости вытекает равновозможность появления любого из чисел 1,2,3,4,5,6.
ОВероятностью события А называется отношение числа благоприятствующих этому событию исходов (исходов, составляющих событие А), к общему числу всех равновозможных исходов в конечномерном пространстве элементарных событий, т.е. P(A) = mn , где m – число благопри-
ятствующих исходов, n – общее число несовместных равновозможных исходов, составляющих пространство исходов.
!Свойства 1 – 4, рассмотренные для статистической вероятности, справедливы и для классической вероятности.
Пример:
При бросании игральной кости из 6 случаев: 1,2,3,4,5,6 событию A – появление не менее 4-х очков, благоприятны случаи 4,5,6, и неблагоприятны
1,2,3.
1.3.2.1. Основные формулы комбинаторики
Рассмотрим наиболее часто встречающиеся при использовании классической схемы ситуации, требующие подсчета общего количества случаев и количества благоприятствующих случаев. При этом используются методы комбинаторики – раздела математики, изучающего задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам.
12 |
Лекции 1-2 |
При рассмотрении следующих ниже схем выбора и получении соответствующих формул используются два важных правила сложения и умноже-
ния.
Пусть множество A , a A содержит n элементов, множество B , b B
– m элементов. Тогда выбор « a или b» можно осуществить n + m способами, выбор « a и b » – n ×m способами.
Действительно, если мы выбираем один элемент из объединения двух множеств A и B , то существует n + m различных возможностей. Если мы выбираем один элемент из A и один элемент из B , то для первого выбора имеется n возможностей, для второго – m возможностей и число различных пар (a,b) равно n ×m .
Эти формулы допускают обобщение. Так, если имеется три множества A , a A, B , b B , C , c C , содержащие соответственно n , m и k элементов, то выбор « a или b или c » осуществляется n + m + k способами, выбор « a и b и c « – n ×m ×k способами, и т.д.
Выборки без возвращения
Пусть имеется множество A , состоящее из n элементов.
ОПодмножество множества A (упорядоченное или неупорядоченное), состоящее из m элементов, где m ≤ n , называется m –элементной выборкой из n –элементного множества (соответственно, упорядоченной или неупорядоченной).
Рассмотрим основные возникающие ситуации.
1) Вычислим число способов упорядочения n – элементного неупорядо-
ченного множества. Первый элемент можно выбрать n различными спо-
собами, второй – n −1 способами, третий – n −2 способами, и т.д. В ре- (n −1) (n −2) ... 3 2 1 = n!зультате получаем – факториал числа n .n
ОУпорядоченная n –элементная выборка из n –элементного множества называется перестановкой. Число перестановок n элементов
Pn = n!.
2) Рассмотрим упорядоченные m –элементные выборки из n – элементного множества, где m ≤ n . Первый элемент можно выбрать n различными способами, второй – n −1 способами, третий – n −2 способами, m –й элемент – n −m +1 способом. Всего различных способов
n (n −1) ... (n −m +1)= |
n (n −1) ... 2 1 |
= |
n! |
. |
|||
|
|
|
|
||||
1 2 ... (n −m) |
|
(n −m)! |
|||||
|
|
|
|||||
ОУпорядоченная m –элементная выборка из n –элементного множества называется размещением из n по m .
Число размещений из n по m :