OMI-3

ін. Оскільки більшість популяцій постійно обновляється, їх харак­ теристики змінюються в часі.

Розглянемо найпростіший випадок моделювання динаміки зміни чисельності (N) гіпотетичної популяції з урахуванням наро­ джуваності і смертності. Народжуваність є середнім числом особин, що народилися в популяції за одиницю часу. Ця величина залежить від багатьох факторів: розміру і складу популяції, фізичних умов навколишнього середовища. Зміна розміру популяції dNp за рахунок народжуваності за деякий проміжок часу At буде дорівнює добуткові коефіцієнта народжуваності кр на розмір популяції і на цей ПРОМІЖОК часу:

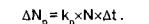(6) Смертність є середнім числом особей, що вмерли в популя­ ції за одиницю часу. Тоді зміна розміру популяції dNC за рахунок

смертності за деякий проміжок часу буде дорівнює:

Відповідно, сумарна зміна розміру популяції за час At дорів­ нює:

(8)

де (kпр =kр - kc) - загальний коефіцієнт приросту популяції. Розділивши ліву і праву частину рівняння на At і перейшовши до границі при dt->0, отримаємо диференціальне рівняння першого порядку:

(9)

де r - "миттєва швидкість росту" популяції без урахування обмеж­ уючого впливу середовища. Ця модель має назву моделі нормаль­ ної репродукції або мальтузіанськой моделлю на ім'я відомого вченого Мальтуса, який у кінці 18 сторіччя уперше підняв питання про ріст чисельності людства.

Рішенням даного диференціального рівняння є експоненціальна залежність розміру популяції N від часу (рис. 4):

(10)

де N() - розмір популяції в деякий початковий момент часу. Експоненціальний рост популяції є характерним при відсут-

ності конкуренції. Наприклад, початкова стадія росту популяції мікроорганізмів на субстраті описується рівнянням, аналогічним

81

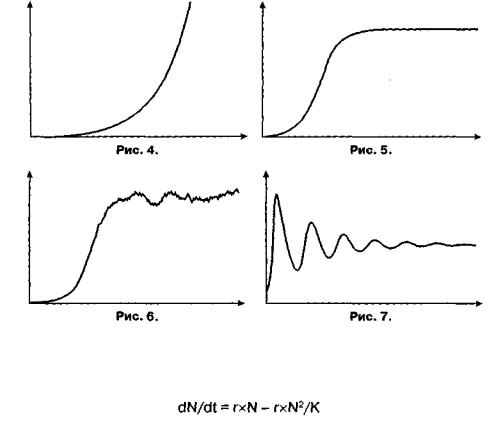
(10), але при наявності конкуренції популяція не росте необме­ жено. П. Ферхгюльст ще в 1838 р. припустив, що процес загибелі організмів спостерігається при зустрічі двох індивідів, тобто від­ бувається через "тісноту".

Існує деяка "межа росту" (К), до якої прагне розмір популяції (рис. 5) або навколо якої він коливається (рис. 6,7).

Такий характер росту популяції добре описують так звані "логістичні" рівняння [8], у яких швидкість росту популяції нелінійно залежить від її розміру:

(11)

На початковій, експоненціальній стадії, швидкість росту попу­ ляції збільшується (рис. 4), потім вона уповільнюється, зупиняєть­ ся, і починає падати (фаза негативного прискорення або виходу на стаціонар). Результати чисельного інтегрування для логістичної моделі представлені на рис. 6. Видно, що система коливається навколо стабільного стану N = К за рахунок випадкових відхилень.

82

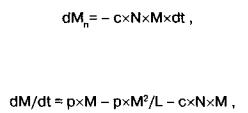
Випадкові відхилення у великих популяціях мають невеликі значення і, практично, не є періодичними. Однак нерідко чисель­ ність великих сукупностей має досить чітку циклічність (рис. 7). Одним з пояснень таких коливань є залежність росту популяції від (нинішніх умов (наприклад, харчування).

4. Математична модель "хижак - жертва"

Аналогічні міркування були застосовані італійським математиком Вольтерра в 1931 р. для моделювання взаємодії двох попу­

­­­­й за принципом хижак-жертва. Вона описує періодичну зміну кількості антагоністичних видів.

Задача моделювання формулюється в таким чином. Нехай у деякому екологічно закритому районі, живуть тварини двох видів. жертви харчуються рослинної їжею, якої є достатня кількість. Хи­ ­­ки можуть харчуватися тільки жертвами. Необхідно визначити, як буде мінятися чисельність жертв (М) і хижаків (N) з часом.

Якщо чисельність популяції хижаків буде описуватися рівнянням (11), то при розрахунках чисельності жертв необхідно врахувати зменшення їх чисельності за рахунок їх поїдання хижаками:

де с - коефіцієнт, що характеризує частоту зустрічей жертв із хижаками. Таким чином, загальне рівняння для жертв буде мати ви-

ГЛЯД:

(12)

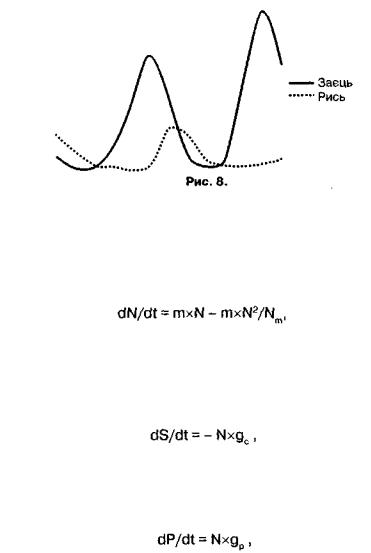
де р - "миттєва швидкість росту" популяції жертв без урахування обмежуючого впливу середовища, L - межа росту, до якої прагне розмір популяції жертв за умови їх окремого від хижаків існування Рішення системи рівнянь (11) і (12) може бути використане для моделювання закономірностей динаміки экосистем на основі конкурентної взаємодії між популяціями різних видів, за прин­ ципом «хижак-жертва», «паразит-хазяїн», «травоїдне-рослина». Наприклад, динаміка коливання чисельності зайця-біляка і канадської рисі (рис. 8) добре описується цією системою, принаймні, на

якісному рівні.

83

5. Моделювання клітинного росту

Рост культури клітин можна описати найпростішим диферен­ ціальним рівнянням, аналогічним (6). Якщо врахувати уповільнен­ ня швидкості росту клітинної культури при великій щільності попу­ ляції, ми дістанемо логістичне рівняння:

(13)

де N - число мікробних кліток, Nm - рівноважний розмір клітинної популяції.

Оскільки субстрат використовується на підтримку життєді­ яльності всіх живих клітин відносно рівномірно, швидкість падіння його концентрації пропорційна числу клітин:

(14)

де gс - миттєва швидкість синтезу субстрату. Звичайно клітинна культура продукує один або кілька корисних продуктів, які можуть впливати на рост самої культури. Швидкість росту концентрації продуктів також прямопропорційна ЧИСЛУ клітин:

(15)

де gр - миттєва швидкість синтезу продукту.

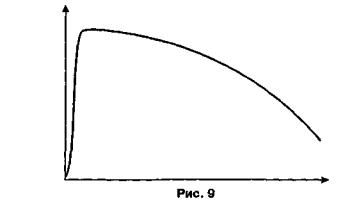
Чисельне інтегрування системи рівнянь (13), (14), і (15) при­ водить до знайомої форми зміни числа клітин у культурі (рис. 9). На ньому розрізняються фази експоненційного росту, виходу на стаціонар і відмирання після виснаження субстрату.

84

6. Математичне моделювання в імунології.

Імунітет - це складний комплекс реакцій організму на вторгнення антигенів - чужорідних об'єктів або клітин, тканин, білків, що переродилися. Специфічна імунна реакція на молекулярно­ му рівні починається з того, що спеціалізовані плазматичні кліти­ ни виробляють у великій кількості білкові молекули - антитіла, які нейтралізують антигени.

Розглянемо модель роботи імунного апарату під час трива­

­­­о інфекційного захворювання. Ця модель використовується в медичній практиці при лікуванні вірусного гепатиту і гострої пнев­ монії.

Взаємодія антигенів і імунних сил організму в математичній моделі має характер, подібний до взаємодії в системі "хижакижертви". "Жертвами" тут є чужорідні об'єкти - антигени з концентрацією X. "Хижаками" є антитіла з концентрацією N, що створються плазматичними клітками з концентрацією Р. Така модель часто використовується в клінічній практиці при лікуванні вірусного і гепатиту, гострої пневмонії та ін. Врахуємо очевидні міркування:

коефіцієнт розмноження антигенів m (вірусів, бактерій) має обернено-пропорційну залежність від температури, що пов'я­ зано із стримуючим впливом високої температури на їх роз­ множення; природний розпад антитіл і антигенів пропорційний їх концен­

траціям з коефіцієнтами nс і mс, відповідно;

85

-природна загибель плазматичних клітин пропорційна їх кон­ центрації з коефіцієнтом рс ;

-взаємодія антиген-антитіло в реакції аглютинації пропорційно імовірності зустрічі відповідного антитіла з антигеном, тобто добутку XxN;

-надходження антитіл до крові пропорційно концентрації плаз­ матичних кліток Р;

-швидкість народження плазматичних кліток є функцією кон­

центрації антигенів F(X) з коефіцієнтом рр, що має прямо-пропо-. рційну залежить від температури.

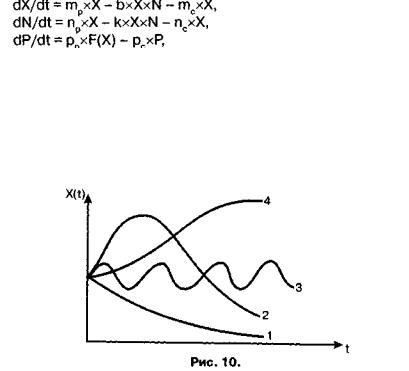
Зурахування цього можна скласти систему диференціальних рівнянь, що описують тривалий процес інфекційного захворювання:

де b - коефіцієнт, що враховує імовірність нейтралізації антигену антитілами при зустрічі з ними; nр - коефіцієнт розмноження анти­ тіл; k - коефіцієнт, що враховує зменшення числа антитіл за раху­ нок їх зв'язку з антигенами,

Дослідження характеру рішень математичної моделі дали чо­ тири основні форми перебігу інфекційного захворювання. На рис. 10 показано можливі випадки динаміки імунної реакції (X - кіль­ кість антигенів, t - час).

Субклінічна форма (1) - проходить без фізіологічних порушень в організмі і без зовнішніх проявів. Засоби імунного захисту легко зни­ щують антигени, не даючи їм розмножитися до небезпечної межи.

86

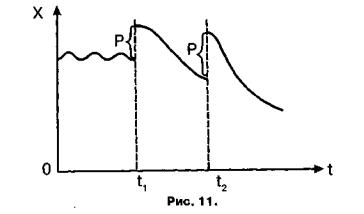
Гостра форма (2) спостерігається коли організм атакується невідомим антигеном у великих кількостях. Спочатку відбувається його інтенсивне розмноження. Коли ж імунна система виробляє проти антигену достатню кількість антитіл, чисельність антигенів різко зменшується.

Хронічна форма (3) - установлюється динамічна рівновага антигенів і антитіл. Виникає стійкий стан хвороби.

Летальна форма (4) - імунна реакція занадто затримується, і ве­ ника кількість антигенів приводить до необоротних змін в організмі.

Дослідження математичної моделі полягає у розв'язанні отриманої системи диференціальних рівнянь при відомих коефіцінтах і з відомими початковими умовами Х(0), N(0), Z(0). Значення коофіцієнтів визначають за результатами спеціальних біохімічних аналізів, для кожної людини вони індивідуальні. Дуже важливо, що така система рівнянь при різних початкових умовах і коефіцієнтах показує абсолютно різну динаміку процесу.

Наприклад, у медичній практиці, лікування деяких інфекційних захворювань проводять методом загострення, тобто переведенням хронічної форми в гостру з наступним одужанням (рис. 11). Для цього потрібно штучно загострити хворобу, тобто ввести в організм у певні моменти часу (t1 t2) певну кількість Р біостимулятора - антигену, який є конкуруючим, непатогенним і не розмножуться. Через деякий час він породжує посилену імунну відповідь, що приводить до швидкого одужання.

87

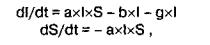
Дослідження математичної моделі на ЕОМ дає змогу визна­ чити кількість біостимулятора і момент часу його введення в орга­ нізм хворого, при яких перебіг хвороби набуває потрібної форми.

Переведення хронічної форми в гостру можна здійснити за допомогою температурного ефекту; гіперчи гіпотермії, оскільки коефіцієнти mр і zр , які відповідають за розмноження антигенів і утворення плазматичних клітин, залежать від температури. Тобто, змінюючи штучно температуру організму чи фізіологічних засобів, які не мають побічної дії на імунну систему, можна досягти потріб­ ного результату. В цьому випадку теж не обійтися без дослідження математичної моделі на ЕОМ. Багаторазове прораховування мо­ делі при різних значеннях температури Т допоможе знайти таку, при якій графік перебігу хвороби набуває потрібної форми.

7. Моделювання епідемічних процесів

Епідемія - саморегулюючий процес взаємодії мінливих гетеро­ генних популяцій паразита і хазяїна. Моделювання конкретних епіде­ мій з метою передбачення масштабів зараження залежить від особли­ востей передачі, плину і результату даного захворювання, вироблення імунітету в перехворілих, складу популяцій хазяїв і паразитів.

Розглянемо найпростіший випадок передачі паразита, що ви­ кликає захворювання з довічним імунітетом, однорідній популяції хазяїна (людина). Позначимо чисельності сприйнятливих (тих, хто ще не хворів) і інфікованих членів популяції через S і І відповідно. Вважаючи, що розмір популяції хазяїна постійний (N = const = S +1 + "ті, що одужали"), а всі немовлята сприйнятливі, дістанемо наступ­ ну систему рівнянь, що описують динаміку поширення епідемії:

(16)

де а - коефіцієнт зараження сприйнятливих; b - коефіцієнт видужання інфікованих; g - коефіцієнт смертності членів популяції Член axIxS визначає число заражених, пропорційне числу зустрічей інфікованих зі сприйнятливими, тобто добуткові їх численностей. Член bxl визначає видужання інфікованих, пропорційне їх числу. Член gxl визначає число померлих (помирають тільки від хвороби) і, відповідно, число народжених сприйнятливих.

88

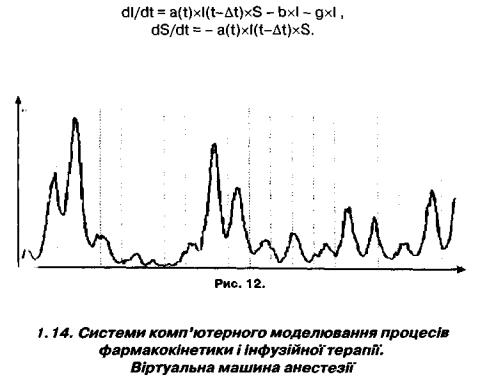
У моделі (16) ми вважали, що людина стає контагіозною від­ разу після інфікування. Однак більшість захворювань мають інку­ баційний період, у який людина ще не заразна. Таким чином, dl/dt запежить не від зустрічей сприйнятливих із інфікованими, а від зустрічей сприйнятливих із членами популяції, що вже стали зараз­ ними. Тобто спостерігається запізнення на час dt. Ще одним важливим доповненням до моделі може бути урахування залежності імовірності інфікування від пори року (а=f(t)), тоді:

(17)

Результат чисельного інтегрування (17), що якісно погоджуться з реальними даними, представлено на рисунку 12.

однією з найважливіших задач медицини є моделювання процесів фармакокінетики, з метою визначення терапевтично обґрунтованих дозувань лікарських речовин в організмі людини. Результатом такого моделювання повинен бути точний розрахунок концентрації фармакологічного препарату в тих чи інших органах і тканинах, що в свою чергу, дасть можливість індивідуальної лікарської терапії,

89

з мінімальним ризиком передозування і побічних явищ, а також економічно обґрунтованими витратами лікарських засобів. Сьогодні існують такі методи вирішення цієї задачі. В результаті клінічних іспитів визначається рівень лікарських речовин у крові пацієнта шляхом багатократного вимірювання концентрації препарату на фоні його тривалого застосування, або в результаті багатократного визначення концентрації препарату протягом визначеного інтервалу часу після його одноразового введеніня. На базі отриманої інформації моделюються процеси, які відбуваються з лікарською речовиною в організмі людини. Будь-яка з відомих моделей фармакокінетичних процесів описується набором громіздких диференційних рівнянь з нечітко визначеними коефіцієнтами (див. розділ «Математичне моделювання»), що має в переважній більшості теоретичний інтерес, так як їх широке використання в клінічній практиці малоймовірне. Як показує дослід, лікар найчастіше розраховує дозування препарату емпірично або за спеціально підготовленими таблицями. В цьому випадку лікарська терапія може бути недостатньо ефективною, а витрати лікарських препаратів нераціональними. Крім того, завжди існує загроза передозування потенційно токсичних препаратів. Наприклад, передозування антибіотику гентаміцину може привести до токсичного ураження канальців нирки, а в деяких випадках може бути ушкоджений слуховий нерв.

Система комп'ютерного моделювання процесів фармакокінетики PharmaKin.Pro дозволяє на основі характеристик фармакологічних , препаратів, визначених в результаті клінічних дослідів і внесених до і бази даних системи, теоретично розрахувати параметри введення, розподілу і виведення лікарських речовин в різних органах і тканинах І організму людини, з урахуванням усіх основних факторів, що впливають на процеси фармакокінетики: біохімічних перетворень, гідродинаміки, осмосу, обміну речовин і води між позаклітинною речовиною і кров'ю, обміну речовин і води між внутрішньоклітинною рідиною і клітинами, виділення речовин нирками, виділення і руйнування речовин печінкою, моделювання функцій шкіри, моделювання функцій органів дихання.

Методика використання системи PharmaKin.Pro в клінічній практиці:

90