Лекции Физика / Лекция 10.б-1
.pdf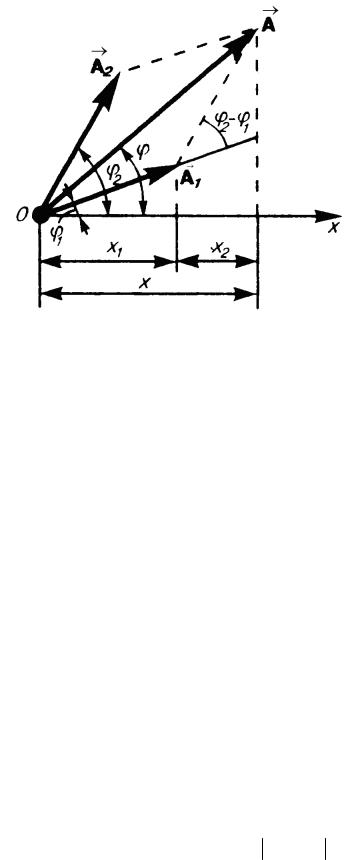
11
Рис.7
Так как векторы A1 и A2 вращаются с одинаковой угловой скоростью ω0 , то разность фаз между ними остается постоянной. Уравнение результирующего колебания будет:
x = x1 + x2 = A cos(ω0t + ϕ) ,
где
A2 = A2 |
+ A2 |
+ 2 A A cos(ϕ |
2 |
− ϕ ) , |
(10.24) |
|||
1 |
2 |
1 |
2 |
1 |
|
|||
tgϕ = |
A1 sin ϕ1 |
+ A2 sin ϕ |
2 |
. |
(10.25) |
|||
A1 cosϕ1 |
|
|
|
|||||
|
|
+ A2 cosϕ2 |
|
|||||
Таким образом, тело, участвуя в двух гармонических колебаниях од- |
||||||||
ного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности
фаз складываемых колебаний. |
|
Выполним анализ выражений (10.24) и (10.25) |
в зависимости от разности |
фаз ϕ2 − ϕ1: |
|
1) (ϕ2 − ϕ1 ) = ±2mπ (m = 0,1,2,...) , тогда A = A1 + A2 , |
т.е. амплитуда результи- |
рующего колебания равна сумме амплитуд складываемых колебаний;
2) (ϕ2 − ϕ1 ) = ±(2m + 1)π (m = 0,1,2,...) , тогда A = A1 − A2 , т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний. При равенстве амплитуд складываемых колебаний амплитуда результирующего колебания равна удвоенной амплитуде каждого колебания, если они разность фаз между ними равна 0 или кратна 2π , и равна 0, если колебания происхо-
12
дят в противофазе. Эффект зависимости амплитуды результирующего колебания от разности фаз ϕ2 − ϕ1 обусловлен интерференцией двух колебаний с одинаковой частотой.
Биения
Особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления незначительно отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны A , а частоты равны ω и ω + ω , причем ω >> ω . Предположим, что начальные фазы обоих колебаний были равны нулю:
x1 = Acos(ω t) |
|
x = Acos(ω + ω)t . |
(10.26) |
2 |
|
Складывая эти выражения с использованием формулы для суммы косинусов и
учитывая, что во втором сомножителе |
1 |
ω << ω , получим: |
|
||
|
|
||||
|
2 |
|
|
|
|
x = x |
+ x = (2 Acos |
ω t) cos(ω t) . |
(10.27) |
||
1 |
2 |
|
|
2 |
|
|
|
|
|
|
|
Результирующее колебание (10.27) можно рассматривать, как гармоническое с частотой ω , амплитуда которого изменяется по следующему периодическому закону:
|
|
ω t |
|
. |
|
|
A |
= |
2 A cos |
|
(10.28) |
||
б |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Такого рода колебания можно условно назвать квазигармоническими, |
||||||
поскольку период изменения амплитуды Aб |
существенно больше периода ко- |
|||||
лебаний 2π ω . Частота изменения |
Aб в два раза больше частоты изменения |
|||||
косинуса (так как берется по модулю), т.е. частота биений равна разности частот складываемых колебаний: ωб = ω . Период биений T = 2π / ω .
На рис.8 представлена зависимость сигнала биений от времени; сплошная кривая - результирующее колебание (10.27) в зависимости от времени, а пунктирная огибающая - медленно изменяющаяся в зависимости от времени в соответствии с уравнением (10.28) амплитуда.
13
Рис.8
Метод биений используется для настройки музыкальных инструментов, анализа слуха и т.д.
Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу
Выполним сложение двух гармонических колебаний одинаковой частоты
ω, происходящих во взаимно перпендикулярных направлениях вдоль осей OX
иOY. Для простоты предположим, чтоб начальная фаза первого колебания равна нулю, и запишем:
x = Acos(ω t) |
, |
(10.29) |
|
||
y = B cos(ω t + α ) |
|
|
где α - разность фаз колебаний, A и B - соответственно амплитуды складываемых колебаний.
Уравнение траектории результирующего колебания можно получить путем исключения из системы уравнений (10.29) времени. Запишем колебания в следующем виде:
x / A = cos(ω t) , y / B = cos(ω t + α ) = cos(ω t) cosα − sin(ω t) sin α ,
и произведем замены во втором уравнении:
cos(ω t) → x / A , sin(ω t) → ±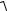
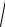1 − (x / A)2 .
После преобразований получим уравнение эллипса на плоскости OXY, являюще-
гося траекторией колеблющейся точки:
|
x 2 |
− |
2xy |
cosα + |
y 2 |
= sin 2 α |
. |
(10.30) |
|
A2 |
AB |
B 2 |
|||||
|
|
|
|
|
|
14
Ориентация осей эллипса относительно осей координат зависит от α .
Рассмотрим некоторые частные случаи, представляющие физический интерес:
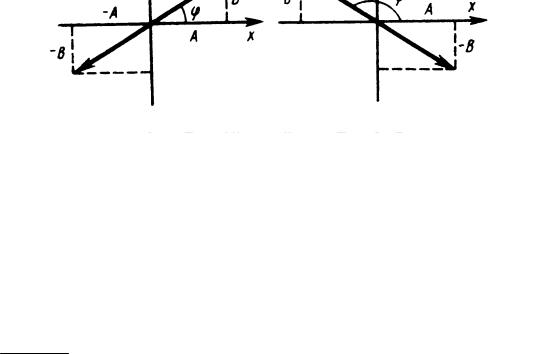
1) α = mπ (m = 0,±1,±2,...) - эллипс вырождается в отрезок прямой y = ±(B / A)x , причем знак «+» соответствует четным значениям m либо 0, а знак «-» - нечетным значениям m (рис.9).
Рис.9
В данном случае говорят о линейно поляризованном колебании. Результирующее колебание является гармоническим колебанием с частотой ω и амплиту-
дой 
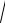A2 + B 2 , совершающимся вдоль прямой, составляющей с осью OX угол
B |
|
|
ϕ = arctg |
|
cos(mπ ) . |
|
||
A |
|
|
2) α = (2m + 1) π (m = 0,±1,±2,...) , уравнение (10.30) примет вид
2 |
|
|
|
|
|
x2 |
+ |
y 2 |
= 1. |
|
A2 |
B 2 |
||
|
|
|
Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис.10).
Кроме того, если A = B , то эллипс вырождается в окружность. Такие колебания называются циркулярно поляризованными или колебаниями, поляризованными по кругу.
15
|
Рис.10 |
При α = + π |
- движение по часовой стрелке; при α = − π - движение против |
2 |
2 |
часовой стрелки.
Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории точки, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз.
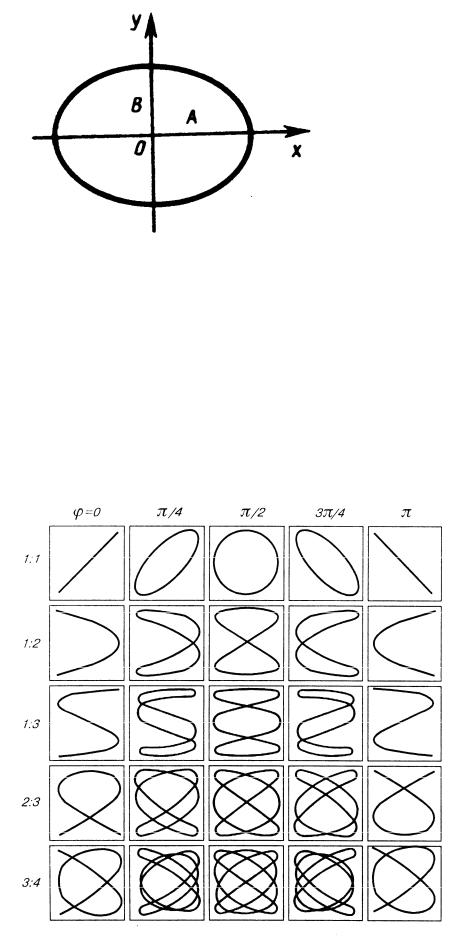
Рис.11
16
На рис.11 приведены фигуры Лиссажу при различных соотношениях частот (слева) и разности фаз (вверху). Амплитуды складываемых взаимно перпендикулярных колебаний полагаются равными.
Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, параллельными осям координат. По виду фигур можно определить неизвестную частоту по известной или определить отношение частот складываемых колебаний. Анализ фигур Лиссажу – широко используемый метод исследования соотношения частот и разности фаз складываемых колебаний, а также формы колебаний.