
- •Статистические методы управления качеством
- •Введение
- •Статистическая грамотность является неотъемлемой составной частью профессиональной подготовки каждого специалиста, имеющего дело с
- •Внастоящее время от работника, занятого в любой области науки, техники, производства, бизнеса и
- •Методы экспертных оценок
- •МОЗГОВАЯ АТАКА
- •МОЗГОВАЯ АТАКА
- •Методы мозговой атаки
- •Методы мозговой атаки
- •Причинно-следственная диаграмма (диаграмма Исикавы)
- •Причинно-следственная диаграмма (диаграмма Исикавы)
- •Пример практического применения диаграммы Исикавы
- •Ранжирование данных
- •Диаграмма Парето
- •Диаграмма Парето
- •Формализация априорной информации
- •Формализация априорной информации
- •Формализация априорной информации
- •Формализация априорной информации
- •Формализация априорной информации
- •Методы обработки выборок
- •Любая группа однородных данных, собранных при измерении параметров – это статистическая совокупность или
- •Б) Характеристики изменчивости (рассеяния) данных в группе:
- •Обработка результатов измерений
- •Обработка результатов измерений
- •Обработка результатов измерений
- •Обработка результатов измерений
- •Обработка результатов измерений
- •Расслоение данных
- •Расслоение данных
- •Расслоение данных
- •Сравнение выборок
- •Сравнение выборок
- •Сравнение выборок
- •Сравнение выборок
- •Гистограммы
- •Гистограммы (виды и расслоение)
- •Гистограммы (сравнение с допуском)
- •Гистограммы
- •Гистограммы
- •Временной ряд
- •Временной ряд
- •Временной ряд
- •Временной ряд
- •Временной ряд
- •Временной ряд
- •Временной ряд
- •Контрольные карты
- •Контрольные карты
- •Контрольные карты
- •Управление технологическим процессом
- •Управление технологическим процессом
- •Управление технологическим процессом
- •Управление технологическим процессом
- •Управление технологическим процессом
- •Корреляционно – регрессионный анализ
- •Диаграммы рассеяния
- •Диаграммы рассеяния
- •Диаграммы рассеяния
- •Корреляция
- •Корреляция
- •Регрессионный анализ
- •Регрессионный анализ
- •Регрессионный анализ
- •Регрессионный анализ
- •Регрессионный анализ
- •Регрессионный анализ
- •Регрессионный анализ
- •Регрессионный анализ
- •Регрессионный анализ
- •Заключение
- •Для управления качеством продукции на производстве специалисты привлекают всё более и более новые

Корреляция
Оценивают степень тесноты (значимость) корреляционной зависимости различными методами.
Так, можно вычислить коэффициент корреляции по формуле:
|
1 |
(xi |
|
)( yi |
|
) |
|
x |
y |
||||
r = |
n |
|
|
|
|
|
|
Sx Sy |
|||||
|
|
|||||
Где х i
х , у
S x и
и у i – значения параметров х и у для i-го измерения; - средние арифметические значения величин х и у; S y – стандартные отклонения величин х и у;
n – число измерений в выборке (объём выборки).
Чем ближе коэффициент корреляции к ±1 (плюс - прямая, минус - обратная связь), тем теснее зависимость между параметрами. Если r = 0 , корреляционная зависимость отсутствует.
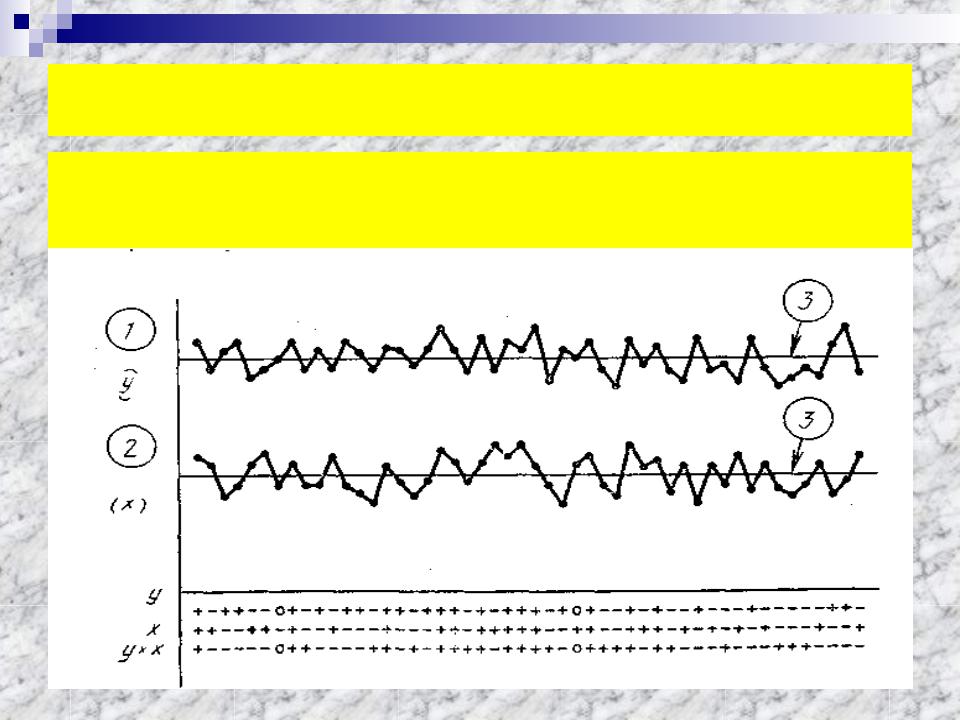
Корреляция
Оценка степени корреляции между праметрами по их временным рядам

Регрессионный анализ
Если корреляционный анализ на основе диаграмм разброса позволяет установить наличие и оценить степень тесноты взаимосвязи двух и более параметров, то регрессионный анализ позволяет выразить установленную взаимосвязь в виде уравнения регрессии, которое кроме возможности рассчитывать характеристику (или результат) у по одному или многим факторам (или причинам) х , даёт тоже достаточно много информации о характере и степени тесноты между исследуемыми параметрами.
Для регрессионного анализа используют данные а к т и в н ы х экспериментов, в ходе которых «раскачивают» технологический процесс, и данные п а с с и в н ы х экспериментов, т.е. результаты текущих наблюдений за процессом. При этом в первом случае возможна «порча» продукции; во втором случае в процесс не вмешиваются, за ним только наблюдают.

Регрессионный анализ
Найти линию регрессии, наиболее адекватно отражающую облако точек – основная задача регрессионного анализа. Естественно, наименьший разброс точек будет около той линии, которая определяется по коррелированным параметрам.
Главное в регрессионном анализе то, что исследователь сам задаёт вид линии регрессии.
Рассмотрим поиск адекватного уравнения на примере уравнений регрессии между содержанием в стекле оксида Fe 2 O 3 (F) и светопропусканием стекла в ИК-области спектра (D) по экспериментальным данным (пассивный эксперимент !), представленным в ранее рассмотренной диаграмме рассеяния. По этой диаграмме мы установили, что связь между этими параметрами существует. Но какая: линейная или криволинейная? – неизвестно.

Регрессионный анализ
Начинают анализ с самой простой формы связи – линейной,
которая выражается уравнением регрессии 1-ой степени и |
|||||||||||
имеет вид |
|
|
|
D a 0 a1 F |
|||||||
|
|
|
|
||||||||
Составляем систему уравнений |
|
|
|
|
|||||||
|
a |
0 |
n a |
1 |
|
F |
D |
||||
|
|
|
|
|
|
||||||
a |
0 |
|
F a |
1 |
F 2 |
|
D F |
||||
|
|
|
|
|
|
||||||
На основе экспериментальных данных подсчитываются соответствующие суммы и подставляются в уравнения системы.

Регрессионный анализ
Решение системы уравнений
методом вычитания |
|
С помощью |
уравнения |
|
программы Solver |
|
|
|
После решения приведённой ранее системы уравнений получим уравнение 1-ой степени
D = 0,92181 – 1,0 F .

Регрессионный анализ
Теперь необходимо оценить, насколько полученное уравнение адекватно экспериментальным данным. Для этого используют критерий, тоже называемый коэффициентом корреляции, но определяемый иначе:
|
R |
1 |
расч |
|
|
|
|
|
|
эксп |
|
|
|
||||
|
(D i эксп D расч ) 2 |
|
|
|
|
(D i эксп |
|
) 2 |
расч |
|
эксп |
D |
|||||
п |
|
n |
||||||
|
|
|
|
|
||||
Для нашего примера после расчёта дисперсий получим следующее значение коэффициента корреляции R = 0.4899.

Регрессионный анализ
Одно из правил оценки адекватности линий регрессии гласит, что дисперсия расчётных по уравнению регрессии данных относительно экспериментальных должна быть на порядок меньше дисперсии экспериментальных данных относительно их средней арифметической (или коэффициент корреляции должен быть больше 0,9 - при хорошо коррелированных параметрах).

Регрессионный анализ
Как и следовало ожидать, судя по диаграмме разброса, адекватность
расчётных и экспериментальных данных мала, а поэтому необходимо продолжить анализ и рассчитать уравнение регрессии 2-ой степени вида:
|
|
|
|
D a a |
1 |
F a |
2 |
F 2 |
|||||||||||||
Составим опять систему уравнений:0 |
|
|
|
|
|
|
|
|
|
||||||||||||
a |
0 |
|
1 |
|
F |
a |
2 |
|
|
F 2 |
|
|
D |
|
|
|
|||||
|
n a |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a |
0 |
|
F a |
1 |
|
F 2 a |
2 |
|
|
F 3 |
|
D F |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
a |
|
|
F 2 |
a F 3 |
|
a F 4 |
|
D F 2 |
|||||||||||||
Подставив в эту |
0систему уравнений1 |
|
численные2 |
|
значения сумм |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
экспериментальных данных и решив эту систему уравнений, получим коэффициенты регрессии для уравнения 2-ой степени:

Регрессионный анализ
D = 0.916211 – 0.976872 F – 0.012245 F 2 .
Для этого уравнения коэффициент корреляции R = 0,6678.
Если бы мы таким же образом рассчитали уравнение регрессии 3-ей степени (кубическая парабола) вида :
D a 0 a1 F a 2 F 2 a 3 F 3
то получили бы следующее уравнение:
D = 0.866938 – 0.64025 F – 0.553823 F 2 – 0.113272 F 3 .
Рассчитав по этому уравнению расчётную дисперсию, получим коэффициент корреляции R = 0,6668.
Делаем вывод, что уравнение 3-ей степени в нашем случае менее адекватно, чем уравнения 2-ой степени, будучи и более сложным в использовании. А поэтому результатом регрессионного анализа принимаем уравнение 2-ой степени.
