Расслоение данных
Можно получить ценную информацию о причинах дефектов, если весь массив данных по участку разделить (расслоить) по станкам. Можно углубить анализ, если массив данных делить поочередно по каждому фактору. Рассматривая факторы первого порядка, можно выявить факторы второго порядка и провести расслоение уже по ним. При необходимости и возможности расслоение можно продолжить и для факторов третьего порядка.
Расслоение данных
► Метод расслоения в чистом виде используется также и в финансово-бухгалтерской сфере (при расчётах стоимости изделия, когда требуется оценка прямых и косвенных расходов отдельно по изделиям и по партиям; при оценке прибыли от продажи изделий отдельно по изделиям и по партиям и т.д.); в сфере маркетинга для оценки поставщиков и потребителей.
► Кроме того, расслоение используется и при использовании других статистических методов: при построении причинно-следственных диаграмм, диаграмм Парето, гистограмм и др.
Сравнение выборок
При предварительном анализе данных наблюдений часто возникает необходимость сравнения двух или нескольких выборок данных, полученных в относительно разных условиях, чтобы решить одинаковы ли они, принадлежат ли одной генеральной совокупности, и тогда эти выборки при необходимости можно объединять для последующего анализа более мощного массива данных; или же выборки неодинаковы, а значит разница между ними не случайна и выборки не могут быть объединены.
Сравнение выборок
Сравнивают выборки по их средним значениям [ 2 ]. Однако это сравнение производится по-разному в зависимости от того, как соотносятся между собой дисперсии этих выборок. Поэтому вначале определяют равны или не равны эти дисперсии.
Сравнение двух дисперсий |
F |
|
n (n |
1)S 2 |
|
1 |
2 |
1 |
|||
|
расч |
|
n (n 1)S 2 |
||
|
|
|
2 |
1 |
2 |
где в числителе должна быть бо'льшая из двух оценок рассеяния (для того, чтобы значение Fрасч всегда было больше 1).
Критическая область для проверяемой гипотезы при уровне значимости α является односторонней и определяется соотношением F расч и F α . Величину F α определяем при уровне значимости α = 0,05 или α = 0,01
Если F расч < F α , значит дисперсии равны (при этом не значит, чтобы были одинаковыми их численные выражения); если же F расч > F α , то дисперсии считаются не равными, и значит разница между выборками не случайна, и существуют какие-то для этого причины.
Сравнение выборок
Сравнение среднеарифметических при равных дисперсиях :
t |
|
|
x1 x2 |
|
|
|
|
|
n1n2 (n1 n2 2) |
|
|
|
|
|
|
|
|
|
|
|
n1 n2 |
|
|
n S 2 |
n |
2 |
S 2 |
|
|
|
|
||||
|
|
|
|
|
|
||||||
1 |
1 |
|
2 |
|
|
|
|
|
|||
Выборки считаются равными, если расчётная величина t оказывается больше, чем (- t α ), и меньше, чем ( t α ), т.е. находится внутри диапазона: - t α < t расч < t α .
Величина t α находится по таблице для t – распределения при уровне значимости α и числе степеней свободы n 1 + n 2 – 2.
Сравнение выборок
Сравнение среднеарифметических при неравных дисперсиях :
|
t |
|
|
x1 x2 |
|
|
|
S12 |
|
|
t (n1 1) |
|
|
S22 |
|
t (n2 1) |
|||||||||
|
|
|
|
t |
|
n1 |
1 |
|
n2 |
1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
S1 |
|
|
S2 |
|
|
|
|
|
|
|
S12 |
|
|
|
S22 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
n1 1 |
n2 1 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n1 1 |
|
n2 |
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где t α (n 1 – 1) – значение при n 1 – 1 степенях свободы и уровне значимости |
|||||||||||||||||||||||||
|
α ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
t α (n 2 – 1) – значение при n 2 – 1 степенях свободы и уровне значимости |
||||||||||||||||||||||||
|
α . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Эти значения находят в таблице. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
В результате, если расчётная величина t' < t" , то с полным |
|||||||||||||||||||||
|
основанием можно говорить о равенстве сравниваемых |
|
|
||||||||||||||||||||||
|
среднеарифметических величинах. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
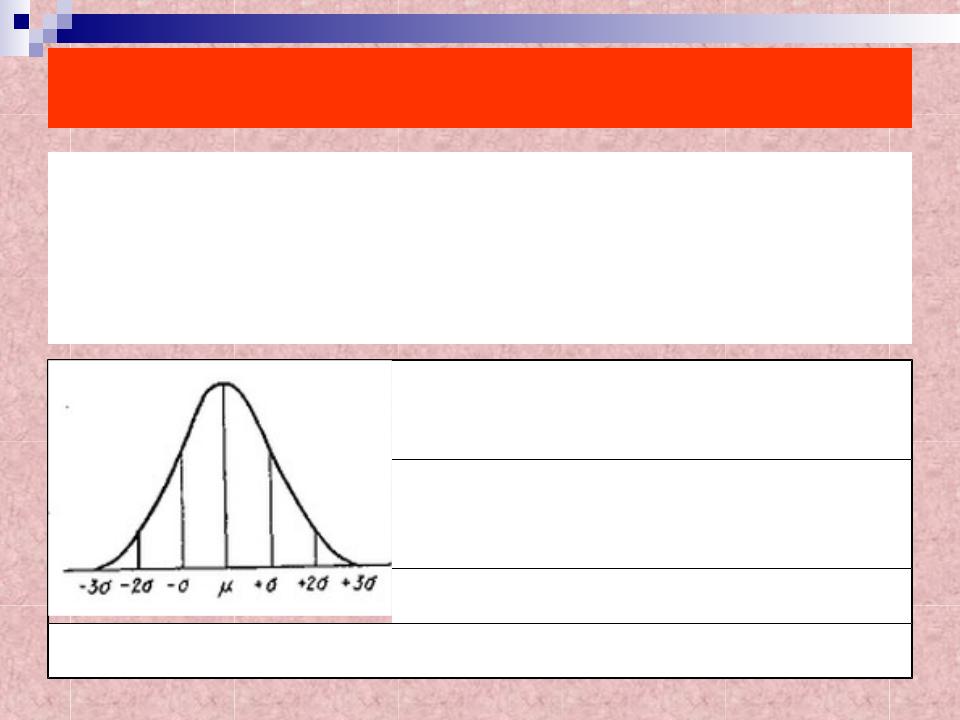
Гистограммы
Если данные из какой либо выборки сгруппировать по частоте попадания в тот или иной интервал значений и представить это распределение графически в виде столбиков соответствующей высоты, получим график, называемый гистограммой (или столбчатой диаграммой). Гистограмма способна дать много информации, если сравнить полученное распределение данных с контрольными нормативами.
|
Частота |
Частота |
|
|
попадания за |
||
Диапазон |
попадания в |
||
пределы |
|||
|
диапазон, % |
||
|
диапазона, % |
||
|
|
Гистограмма нормального распределения
μ ± 1 σ |
68,2 |
31,74 |
μ ± 2 σ |
95,44 |
4,56 |
μ ± 3 σ |
99,73 |
0,27 |
μ ± 4 σ |
99,994 |
0,006 |
Гистограммы (виды и расслоение)
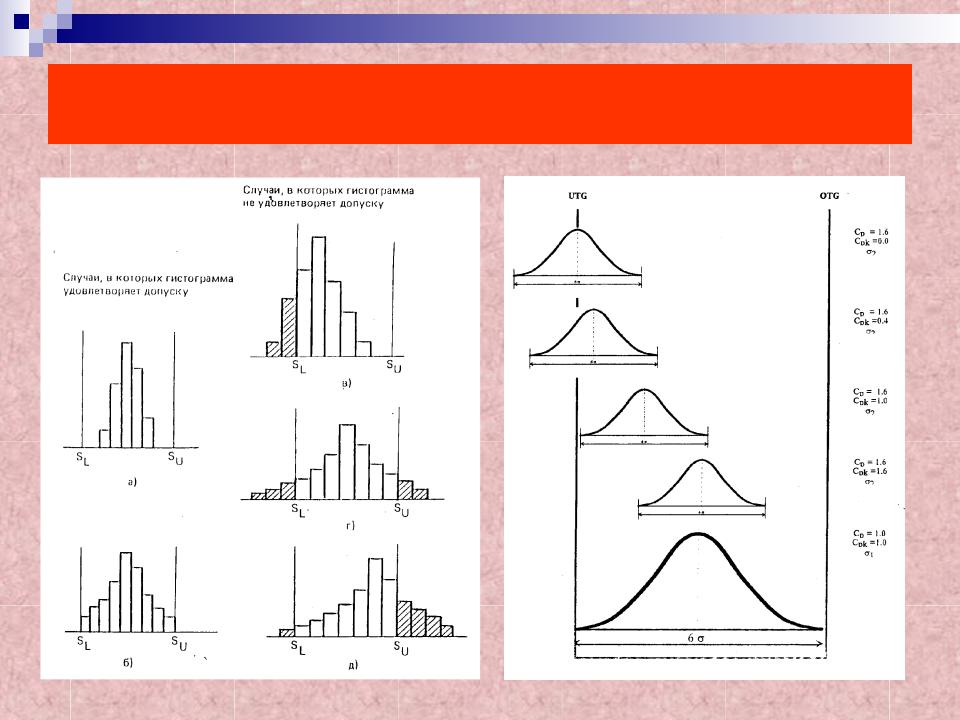
Гистограммы (сравнение с допуском)
Гистограммы
► Существует индекс возможностей (или показатель мощности) процесса, по значению которого можно делать заключение о состоянии разброса по отношению к допуску; о том, достаточен ли допуск.
В том случае, когда есть и верхняя, и нижняя границы допуска и гистограмма выборки расположена между ними, индекс возможностей процесса С р определяется по формуле:
Ср SU SL
6s
где S U - верхняя граница допуска,
S L - нижняя граница допуска,
s - стандартное отклонение выборки.