11. Уравнение состояния

В состоянии равновесия давление жидкости (или газа) p меняется с изменением ее плотности ρ и температуры T. Оно однозначно определяется значениями этих параметров. Соотношение

p=f(ρ,T)

между давлением, плотностью и температурой в состоянии равновесия называется уравнением состояния.

Для капельных жидкостей уравнения состояния очень сложны и поэтому в большинстве гидравлических расчетов принимают его в предельно простой форме

ρ = соnst, (11.1)

(т.е. плотность капельных жидкостей имеет постоянное значение).

Для газов (воздух, природный газ, перегретый пар) уравнение состояния при относительно небольших температурах и давлениях принимает такую форму

pV=RT, (11.2)

где p – абсолютное давление; Т – термодинамическая температура, К; V-удельный объем, связанный с плотностью соотношением V=1/ρ; R – универсальная газовая постоянная: для воздуха R = 287 Дж/(кг.К).

Уравнение состояния может быть записано в виде (с учетом V=1/ρ)

p/ρ=RT. (11.3)

Это уравнение позволяет определить плотность газа при данном давлении и известной температуре. Зная уравнение состояния,возможно определить фактически все основные параметры и характеристики жидкой среды. В частности, для газов коэффициент объемного сжатия определяется при Т= соnst , а коэффициент температурного расширения при p= соnst.

Имея в виду уравнение состояния идеального газа, можно описать процессы изменения его состояния.

1. Изотермический процесс. В этом случае температура газа не меняется, т.е. Т=const на протяжении всего процесса, тогда

= RT = const.

Изотермический процесс возможен лишь при идеально хорошем обмене теплом между газом и внешними телами.

2. Адиабатический процесс – происходящий без обмена теплом с окружающими телами.

Уравнение адиабаты

pV^k = const

или

= const.

Последнее уравнение часто представляют в виде

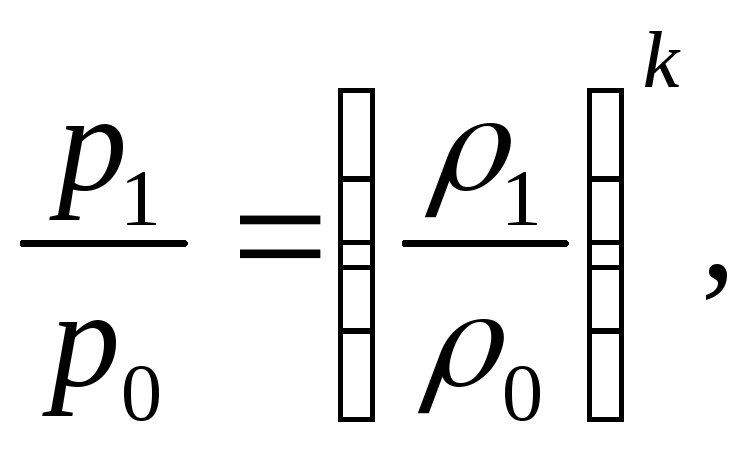
где k – коэффициент адиабаты.

3. Политропный процесс. Изотермический и адиабатический процессы являются идеальными, которые на практике осуществить нельзя, к ним можно только приблизиться. Изотермический процесс должен происходить бесконечно медленно, адиабатический процесс может протекать с конечной скоростью, но в адиабатной, теплонепроницаемой оболочке.

В природе происходят реальные процессы, являющиеся промежуточными между адиабатическими и изотермическими. Такие процессы называются политропными. Чтобы определить такой процесс, необходимо наложить на него только одно ограничение: считать, что повышение температуры тела пропорционально сообщенному телу количеству тепла ∆Q или, что то же, теплоемкость тела при политропном процессе постоянна, т.е.

∆Q = с ·∆T,

где с – const.

Для политропных процессов справедливы те же формулы, что и для адиабатических, например

= const,

где γ имеет значение, промежуточное между с_p/c_v и единицей.

Задача 11.1. Определить коэффициент объемного сжатия для газов в изотермическом процессе (Т= соnst).

Решение. Имея в виду определение коэффициента βр в виде (8.1) и уравнение состояния (11.2) находим dW/dp (в данном случае через W обозначаем объем во всех зависимостях). Из (11.2), W=RT/p, при Т=соnst ,

dW/dp=(-RT/p²)

и окончательно

βр=1/p(при T=const).

Задача 11.2. Определить значение коэффициента температурного расширения для газов в изобарном процессе (при р= соnst).

Задача 11.3. По трубе подается воздух, его температура t = 15C, давление по манометру, присоединенному к трубе в некотором сечении равно P_M=39 кПа. Атмосферное давление p_ат = 735 мм рт.ст. Определить плотность воздуха в данном сечении.

Решение. Определим плотность воздуха с помощью уравнения состояния (11.3)

.

Давление p в числителе складывается из атмосферного давления p_ат = 735 мм рт.ст. = 97960,8 Па и избыточного p_М = 39000 Па = 39 кПа. Результирующее давление p равно p = 136960,8 Па. Плотность воздуха определится так

кг/м³.