9. Идеальная жидкость

Решение дифференциальных уравнений, описывающих движение реальной жидкости, в большинстве случаев затруднительно, поэтому в гидродинамике и гидравлике используют различные упрощенные модели среды; одной из таких моделей является идеальная жидкость. Под идеальной жидкостью понимают воображаемую жидкость, обладающую абсолютной подвижностью (т.е. лишенную вязкости), абсолютно несжимаемую. Такое определение имеет смысл только для капельных жидкостей; идеальный газ также лишен вязкости, но сжимаем (подробнее об этом в п. 11). Для идеальной жидкости μ=0 и =0 и при движении ее всякое трение отсутствует. И, следовательно, отсутствует переход механической энергии в тепловую за счет вязкости (иногда говорят, что «потерь» механической энергии нет). На основании (6.3) видно, при каких условиях трение внутри жидкости отсутствует, т.е.

τ=0.

1. μ=0 – идеальная жидкость;

2. U=0 – жидкость покоится;

3. dU /dу = 0 - эпюра скорости представляет собой прямую линию, перпендикулярную к направлению течения.

Выводы, полученные с использованием модели идеальной жидкости, приходится, как правило, корректировать, вводя поправочные коэффициенты.

10. Поверхностные явления в жидкостях

Молекулы жидкости, расположенные у поверхности контакта с другой жидкостью, газом или твердым телом, находятся в условиях, отличных от условий внутри объема жидкости. Внутри объема молекулы окружены со всех сторон такими же молекулами, вблизи поверхности – лишь с одной стороны. Такого типа несимметричное взаимодействие приводит к особым свойствам поверхностного слоя жидкости.

П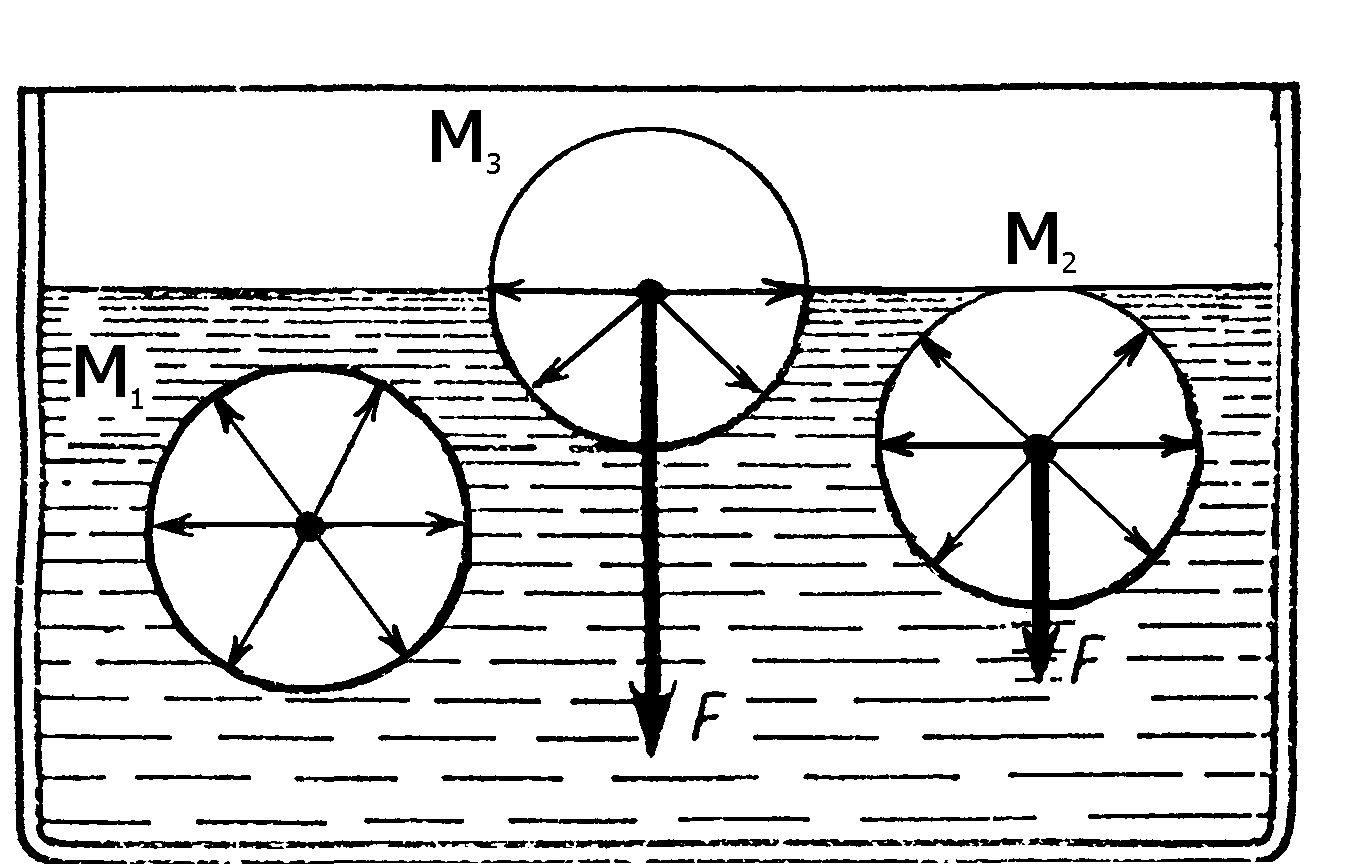оверхностная энергия.Для молекулыM₁, находящейся внутри жидкости (рис. 10.1), условия взаимодействия ее с остальными молекулами одинаковы и поэтому равнодействующая всех сил взаимодействия, действующих на эту молекулу, равна нулю (молекулы жидкости непрерывно колеблются относительно некоторых положений и поэтому, говоря о силе, имеем в виду ее среднее значение). На молекулы, находящиеся в поверхностном слое, например на молекулыM₂иM₃, действуют соседние молекулы, расположенные в этом слое и под ним. Поэтому равнодействующаяFсил, приложенных к каждой молекуле поверхностного слоя, не равна нулю и направлена внутрь жидкости. Следовательно, чтобы вывести молекулы, находящиеся внутри жидкости, на ееповерхность, нужно преодолеть

Рис. 10.1 противодействие молекулярных

сил, т.е. произвести работу. При обратном переходе на глубину потенциальная энергия, которой обладала молекула в поверхностном слое, переходит в кинетическую энергию молекулы. Таким образом, молекулы в поверхностном слое обладают дополнительной потенциальной энергией; эта энергия часто называется свободной энергией.

Изменение свободной энергии ∆П(∆Правно работе по изменению площади свободной поверхности) прямо пропорционально изменению площади свободной поверхности∆S

∆П = σ · ∆S

или

A = σ · ∆S. (10.1)

Эта работа должна еще зависеть от рода жидкости и внешних условий, например, от температуры. Эту зависимость и выражает коэффициент σ.

Величина σ, характеризующая зависимость работы молекулярных сил при изменении площади свободной поверхности жидкости от рода жидкости и внешних условий, называется коэффициентом поверхностного натяжения жидкости.

Свободная поверхность жидкости стремится к минимальному значению для данных условий, например, отдельные частицы – капли – принимают форму шара. Наблюдаемая тенденция к уменьшению поверхности согласуется с обычным стремлением всякой механической системы к устойчивому равновесию, связанному с минимумом потенциальной энергии. В системе СИ величина σизмеряется в Дж/м².

Сила поверхностного натяжения.МолекулаM₃(рис. 10.1), расположенная на поверхности жидкости, взаимодействует не только с молекулами, находящимися внутри жидкости, но и с соседними молекулами на поверхности; поэтому силы взаимодействия направлены вдоль поверхности жидкости.

С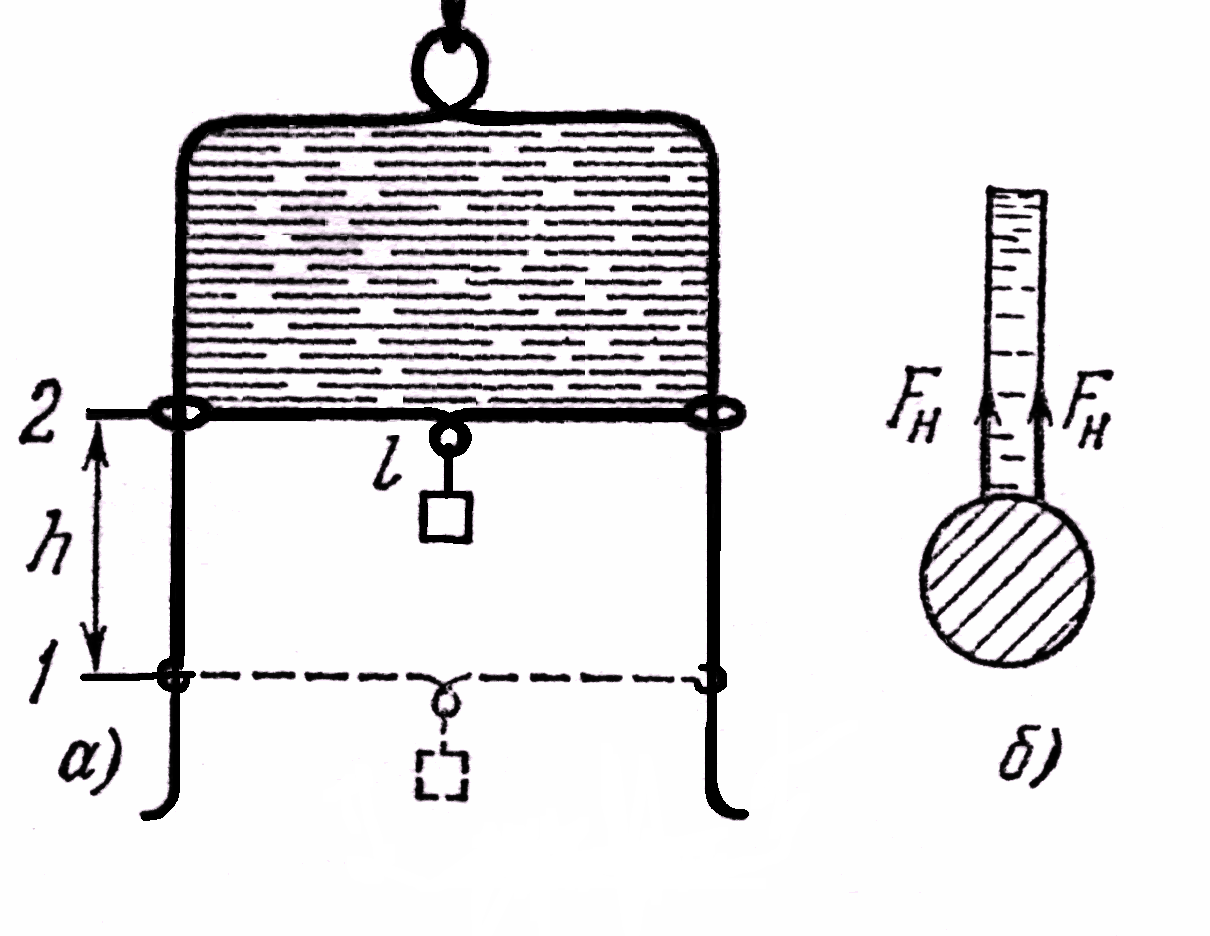илаF, обусловленная взаимодействием молекул жидкости, вызывающая сокращение площади ее свободной поверхности и направленная по касательной к этой поверхности, называется силой поверхностного натяжения. Молекулярныесилы притяжения направлены перпендикулярно любому контуру на этой поверхности.

Для установления связи силы поверхностного натяжения с длиной линии соприкосновения поверхностного слоя рассмотрим проволочную рамку (рис. 10.2), у которой поперечина длиной lподвижная.Рис. 10.2

Рамку затягивают мыльной пленкой, опуская ее в мыльный раствор; после извлечения ее из раствора поперечина lперемещается вверх. Работа, совершаемая силами поверхностного натяжения при перемещении поперечиныlиз положения 1 в положение 2, выражается формулой (10.1)A = σ · ∆S.Так как в нашем случае у слоя пленки две граничные поверхности (рис. 10.2, б), то суммарное сокращение площади∆Sсвободной поверхности равно2hl,поэтомуA =σ · 2hl.С другой стороны, работуAможно найти, умножив силу на путь: общая сила равна2F_HиA=2F_H · h.Таким образом,2F_H · h = σ · 2hlили

F_H = σ · l, (10.2)

откуда

σ =. (10.3)

Единицей σв СИ служит Дж/м², но

1= 1= 1,

что следует непосредственно из (10.3).

Теперь понятны причины, по которым жидкость принимает форму, при которой площадь ее свободной поверхности оказывается наименьшей: силы молекулярного давления втягивают молекулы с поверхности внутрь жидкости, а силы поверхностного натяжения сокращают площадь свободной поверхности. Значения σ для некоторых жидкостей следующие (при комнатной температуре): ртуть – 0,490 Н/м, вода – 0,073 Н/м, спирт – 0,023 Н/м. Примеси сильно влияют на величину σ; например, растворение в воде мыла снижает ее коэффициент поверхностного натяжения до 0,045 Н/м.

Смачивание. Краевой угол. Если опустить стеклянную палочку в ртуть и вынуть ее, то ртути на ней не окажется. Если эту же палочку опустить в воду, то после вытаскивания на ней останется небольшое количество воды. Этот опыт показывает, что молекулы ртути притягиваются друг к другу сильнее, чем к молекулам стекла (ртуть не смачивает стекло), а молекулы воды притягиваются друг к другу слабее, чем к молекулам стекла (вода смачивает стекло). Если капнуть на горизонтальную пластину исследуемую жидкость, то капля расположится либо как показано на рис. 10.3, либо так, как на рис. 10.4. В первом случае

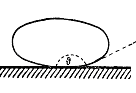
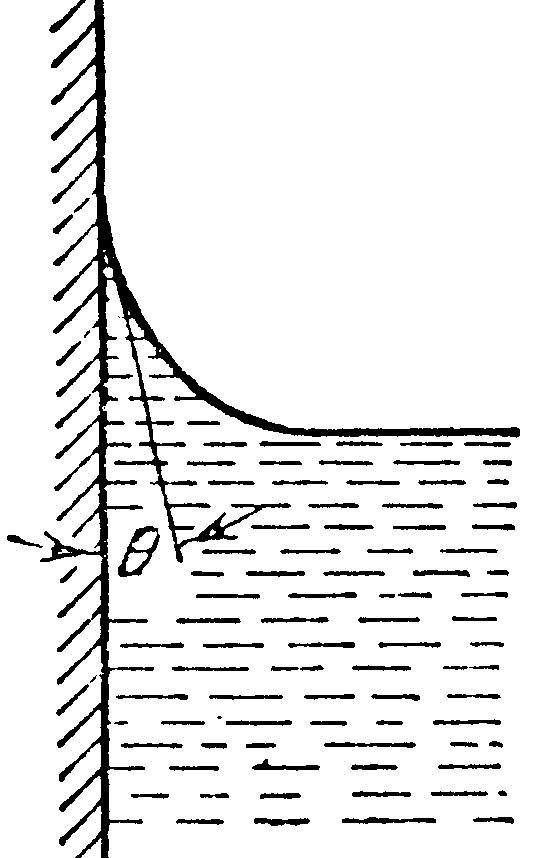
Рис. 10.3 Рис. 10.4 Рис. 10.5 Рис. 10.6

жидкость смачивает твердое вещество, а во втором – нет. Отмеченный на рис. 10.3 угол θ называют краевым углом. Для смачивающих жидкостей он острый, а для несмачивающих – тупой. Поскольку краевой угол θ сохраняется при вертикальном положении твердой поверхности, то смачивающая жидкость у краев сосуда, в который она налита, приподнимается, (рис. 10.5), а несмачивающая жидкость опускается, (рис. 10.6). Мерой смачивания обычно служит косинус краевого угла, т.е. cos θ. При θ = π (cos θ) = -1 говорят о полном несмачивании, при θ = 0 (cos θ = 1) – о полном смачивании.

Мениск. Давление, создаваемое искривленной поверхностью жидкости. Искривление поверхности жидкости у краев сосуда наблюдается в опытах; особенно отчетливо это видно в узких трубках, где искривляется вся свободная поверхность. В трубке с круглым сечением эта поверхность представляет собой часть поверхности сферы и называется мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 10.7, а), а у несмачивающей выпуклый – (рис. 10.7, б). Если поверхность жидкости не плоская, то стремление ее к сокращению приведет к возникновению давления р_λ, дополнительного к тому, которое испытывает жидкость с плоской поверхностью. В случае выпуклой поверхности это дополнительное давление положительно (рис. 10.8, а), в

а б а б

Рис. 10.7 Рис. 10.8

случае вогнутой поверхности – отрицательно, (рис. 10.8, б). Для сферической формы свободной поверхности жидкости с радиусом R это давление выражается формулой

р_λ = . (10.4)

Капиллярность. Искривление поверхности жидкости в узких трубках приводит к кажущемуся нарушению «закона» сообщающихся сосудов. Если в воду опустить узкую стеклянную трубку, то вода втягивается в трубку и ее уровень располагается на высоте h над уровнем воды в сосуде. Объясняется это тем, что давление р_λ в трубке направлено вверх.

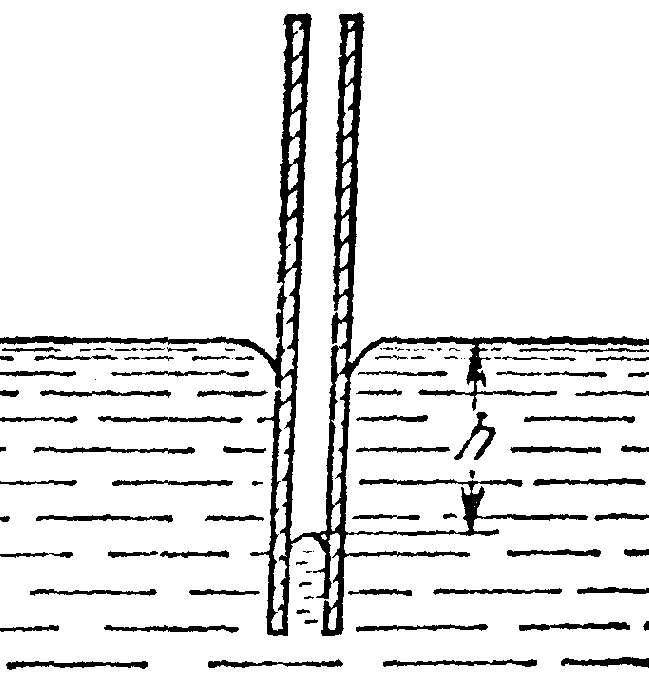
Рис. 10.9 Рис. 10.10

При полном смачивании

h = (10.5)

где r – радиус трубки; – плотность жидкости,σ – коэффициент поверхностного натяжения, g – ускорение силы тяжести.

Смачивающая жидкость в тонких трубках (капиллярах) поднимается вверх (рис.10.9), а несмачивающая – опускается вниз (рис. 10.10). Явления, обусловленные втягиванием смачивающих жидкостей в капилляры или выталкиванием несмачивающих жидкостей из капилляров, называются капиллярными явлениями.

Проявление поверхностных явлений в природе и технике. Во всех растениях и деревьях влага из почвы по капиллярам поднимается до вершин, где через листья испаряется в атмосферу. В почве имеются капилляры, которые тем уже, чем плотнее почва. Вода по этим капиллярам поднимается до поверхности и испаряется, а земля становится сухой. Если рано весной землю вспахать, то капилляры будут разрушены, подпочвенная влага сохранится, и урожай будет увеличен.

Процессы, связанные с кровообращением, определяются капиллярностью, так как мелкие кровеносные сосуды являются капиллярами.

В технике поверхностные эффекты учитываются и используются. Например, для изоляции кирпичной стены от сырости между фундаментом и стеной делают прокладку из вещества, в котором нет капилляров. По тонким капиллярным каналам в фитиле керосин поднимается из резервуара к горелке.

При очистке питьевой воды методом флотации через обрабатываемую воду пропускают пузырьки воздуха. Частицы загрязнений прилипают к пузырькам, всплывают вместе с ними на поверхность и образуют пену, которая затем удаляется.

Учет поверхностного натяжения необходим при расчетах капельных и пленочных оросителей в градирнях, применяемых в системах водоснабжения промышленных предприятий.

Поверхностное натяжение объясняет многие явления, характерные для жидкого состояния вещества, например, образование капель при вытекании жидкости сквозь малое отверстие, образование пены. Известно, что мыльная вода особенно легко дает тонкие пленки, хотя коэффициент поверхностного натяжения мыльной воды значительно меньше коэффициента поверхностного натяжения чистой воды. Это объясняется большой вязкостью мыльной воды, благодаря чему она стекает под влиянием силы тяжести медленнее, чем чистая вода и поэтому легче удерживается между поверхностными слоями.

З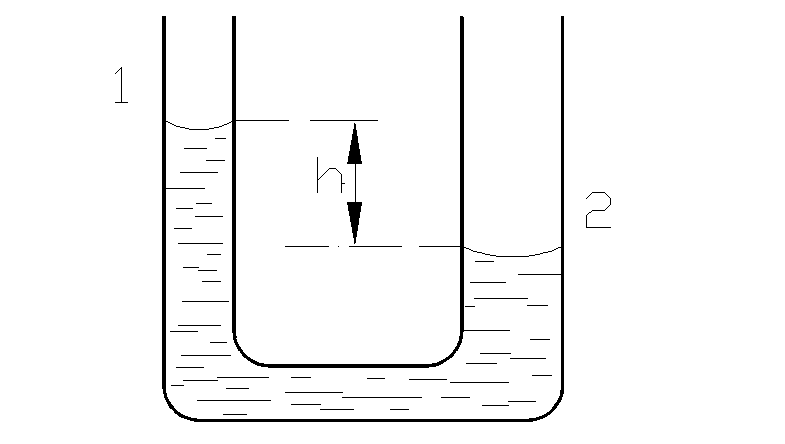адача 10.1.Диаметры колен U-образной стеклянной трубки (рис. 10.11), равны 1 мм и 4 мм. Чему равна разность уровней воды в обоих коленах?

Решение. Давление, создаваемое вогнутой поверхностью воды в более узком колене трубки, уравновешивается давлением, создаваемым разностью уровней воды в обоих коленах h (рис. 10.11) и давлением р₂, создаваемым вогнутой поверхностью в более широком колене Рис. 10.11

p₁ = ρgh+p₂, (10.6)

где ρ – плотность воды; g – ускорение силы тяжести.

Предполагаем, что краевой угол равен нулю, т.е. θ=0, тогда из (10.4) получаем

p₁ = , p₂ = ,

где r₁ и r₂ – радиусы трубок колен.

Вводя вместо радиусов диаметры, получим

p₁ = , p₂ = .

Подставляя последние выражения в (10.6), получим

= ρgh + ,

откуда

h = (-) = (-) = 0,023 м ≈ 23 мм