Постановка задач для решения уравнения Лапласа

П

Рис. Д.2.8

ри решении уравнения Лапласа наиболее часто встречаются следующие краевые задачи (уравнение Лапласа на плоскости относительно потенциала скорости или функции тока). Например, на рис. 1.4, б с помощью линий тока изображена картина обтекания плоской пластины, установленной перпендикулярно потоку.

Первая краевая задача (задача Дирихле)

На границе области Г, рис. Д.2.8 задана непрерывная функция f(x,y). Требуется найти, функцию (или), удовлетворяющую внутри области течения уравнению Лапласа и принимающую на границе Г заданные значенияf(x,y).

Вторая краевая задача (задача Неймана)

На контуре Г, ограничивающем область течения, задана непрерывная функция P(x,y). Требуется найти функцию (или), удовлетворяющую внутри области течения уравнению Лапласа, нормальная производная которойилина границе принимает заданные значенияP(x,y).

Таким образом, непосредственное определение поля скоростей заключается в решении уравнения Лапласа (9.10) или (Д.2.7) для определения φ(x,y) или ψ(x,y), удовлетворяющих граничным условиям данной задачи. Однако в большинстве практических случаев это является невыполнимой задачей. В связи с этим применяется косвенный способ решения задач. Выбирается произвольный потенциал скорости φ(x,y), который удовлетворяет уравнению Лапласа, и строится картина линий тока. Если находятся линии тока, которые совпадают с твёрдыми поверхностями канала или обтекаемого тела, то выбранная функция удовлетворяет граничным условиям задачи и является её решением. В этом случае поле скоростей определяется по формулам

, ,.

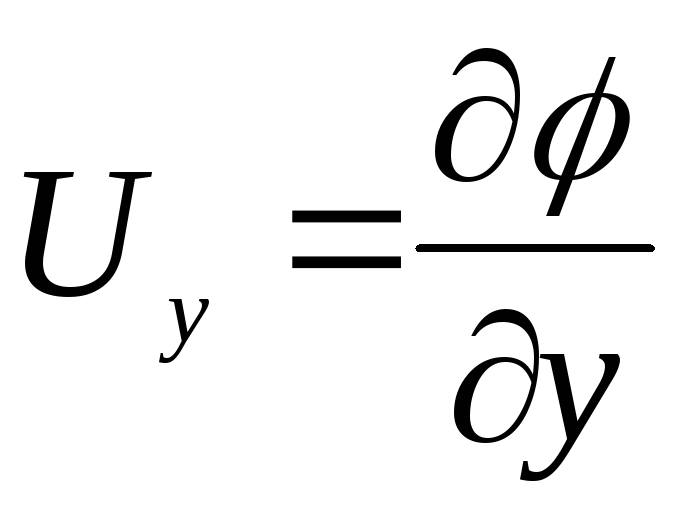Если же не будут найдены линии тока, совпадающие с твёрдыми поверхностями, то выбранная φ(x,y) не является решением задачи; угадывание решений достаточно сложных задач невозможно.

Д.3. Вихревая линия и вихревая трубка. Теоремы о вихрях

Векторы вихря образуют векторное поле, в котором могут быть найдены векторные линии и векторные трубки.

Линия, в каждой точке которой вихри вектора скорости (rot) или векторы угловых скоростей вращения частиц касательных к ней, называется вихревой линией. Уравнение вихревых линий, по аналогии с линией тока, будет

. (Д.3.1)

Если в пространстве, заполненном вихрями, взять некоторый замкнутый контур (не являющийся вихревой линией) и через каждую точку этого контура провести вихревые линии, то образуется вихревая поверхность. Часть жидкости, ограниченная этой поверхностью, называется вихревой трубкой. Когда замкнутый контур бесконечно мал, вихревая трубка называется элементарной.

Из определения вихревой линии и вихревой поверхности следует, что в любой точке таких линий и поверхностей нормальная составляющая вихря скорости равна нулю.

Напомним связь между вектором вихря скорости rot и вектором угловой скорости вращения

,

введем представление о потоке вектора вихря скорости

и учтём известный из векторного анализа факт, что поток любого вектора через любую замкнутую поверхность, внутри которой нет особенностей, равен нулю.

Поэтому и поток вектора вихря по любой замкнутой поверхности тоже равен нулю, т.е.

. (Д.3.2)

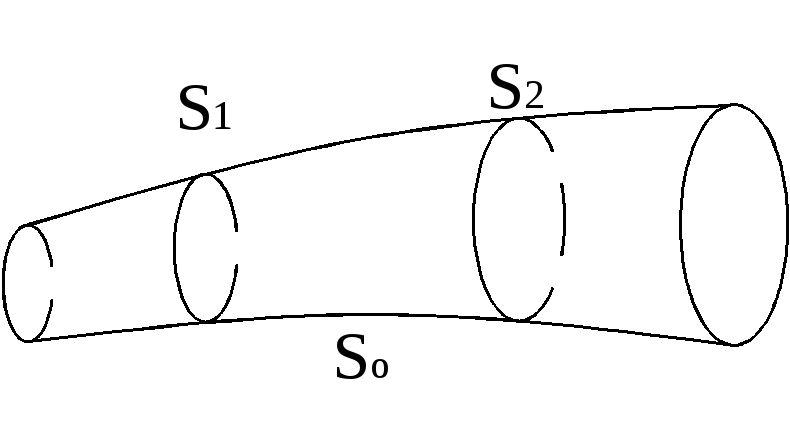
В

Рис. Д.3.1

ыделим в вихревой трубке, рис. Д.3.1, некоторую замкнутую поверхность, образованную двумя любыми поперечными сечениямиS₁ и S₂ и боковой поверхностью S₀.

Так как поток вихря по боковой поверхности равен нулю, то согласно формуле (Д.3.2)

. (Д.3.3)

Из предыдущего равенства вытекает свойство вихревых трубок, известное в кинематике как вторая теорема Гельмгольца: поток вектора вихря скорости через любое поперечное сечение вихревой трубки в данный момент времени постоянный вдоль всей трубки.

Из этой теоремы следует, что поток вихря есть величина, характерная для всей вихревой трубки, поэтому поток вихря принимают за характеристику вихревой трубки и называют интенсивностью

. (Д.3.4)

В основной части вихревая трубка называлась вихревым шнуром, зависимость (10.1) эквивалентна (Д.3.4).

Если величина вихря постоянна по сечению вихревой трубки, то вторую теорему Гельмгольца можно записать в виде

. (Д.3.5)

Из этой формулировки вытекают важные следствия:

1. Сечение вихревой трубки нигде не может стать равным нулю, так как в этом случае скорость вращения частиц должна стать бесконечно большой, что физически невозможно;

2. Вихревые трубки не могут заканчиваться внутри жидкости: они либо замыкаются на себя, образуя вихревые кольца, либо «опираются» на стенку или на свободную поверхность. К последнему типу вихрей относятся наблюдаемые в природе водяные и воздушные смерчи.

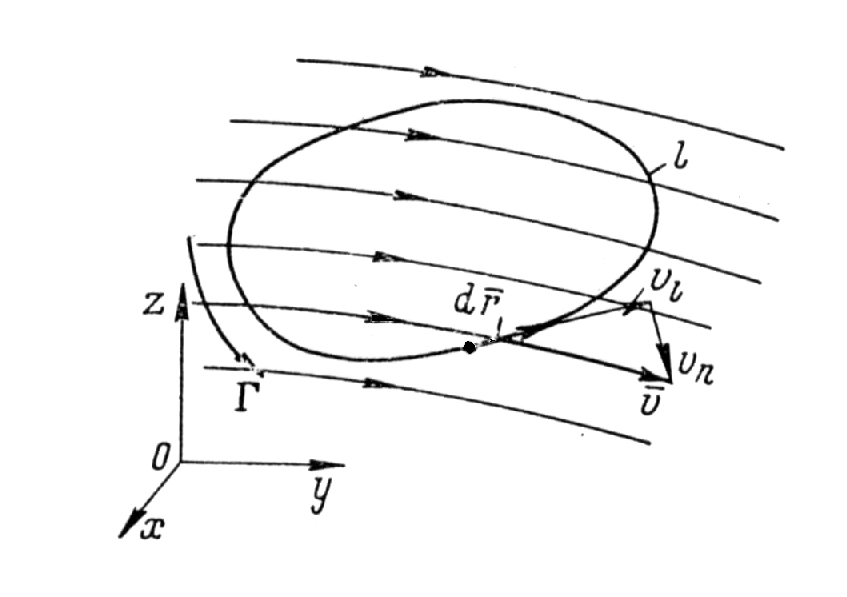
П

Рис. Д.3.2

ри рассмотрении вихревых движений важное значение имеет понятиециркуляции. Она представляет собой криволинейный интеграл по произвольному замкнутому контуру l от скалярного произведения вектора скорости на бесконечно малый элемент контура, рис. Д.3.2.

, (Д.3.6)

г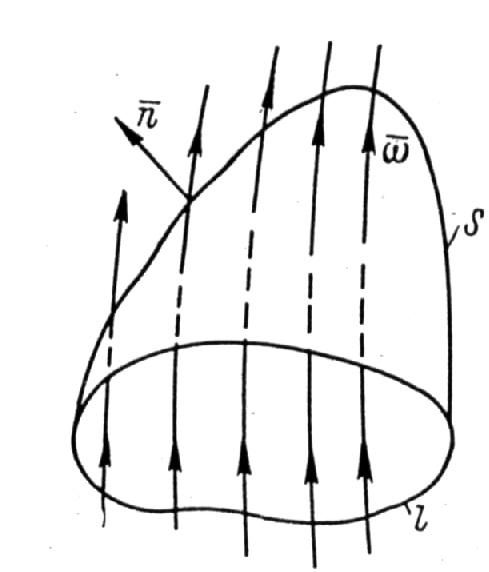де черезU_l обозначена касательная составляющая скорости, а – элемент длины контура.

В соответствии с (Д.3.6) размерность циркуляции , т.е. та же, что и интенсивности.

С

Рис. Д.3.3

вязь между циркуляцией и интенсивностью устанавливается теоремой Стокса. Рассмотрим поток вектора вихрячерез произвольную незамкнутую поверхностьS, рис. Д.3.3, обозначив через l замкнутый контур, на который опирается эта поверхность. Теорема Стокса (приводимая здесь без доказательства) устанавливает такую связь

(Д.3.7)

и формулируется так: поток вектора вихря через произвольную незамкнутую поверхность равен циркуляции скорости по контуру, на который опирается эта поверхность.

Следовательно, согласно теореме Стокса, интенсивность вихревой трубки равна циркуляции скорости по контуру площади её поперечного сечения S. Если считать, что вне вихревой трубки жидкость не завихрена (), то контурl сечения вихревой трубки можно деформировать в произвольный контур l₁, находящийся в жидкости и охватывающий вихревую трубку.

Задача Д.3.1.Определить, является ли турбулентное течение в круглой трубе вихревым, если скорость по сечению распределяется по закону

,

где U– скорость жидкости в точке, удалённой на расстояниеrот оси трубы;– радиус трубы;– некоторая скорость.

Решение.Направляем оси декартовой системы координат так, чтобы ось абсцисс (OX) совпадала с осью трубы. Тогда расстояние от оси трубы до рассматриваемой точки определится так

,

и проекции скорости будут такие

,

, .

Имеем также

,

.

Применяя зависимости (9.5), получаем окончательно

,

.

Таким образом, турбулентное течение в круглой трубе является вихревым.