7. Уравнение неразрывности

в дифференциальной форме

О

Рис. 7.1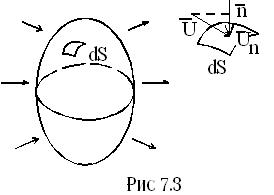

чевидно, что в любой точке внутри потока жидкость не возникает и не исчезает, поэтому можно считать что в любой точке должны выполняться определённые соотношения, содержащие скорость и выражающие закон сохранения массы. Для вывода уравнения такого рода представим внутри потока воображаемую неподвижную замкнутую поверхность, через которую может свободно протекать жидкость. Положительное направление нормали ориентировано внутрь поверхности, рис. 7.1. Любой бесконечно малый элементэтой поверхности, ввиду его малости можно рассматривать как плоскую площадку и скорость в её пределах считать неизменной. Кроме того, на каждой площадке определён вектор нормалик ней. Составим для каждого элемента поверхностипроизведение

,

которое можно представить как

,

где – проекция скорости на нормаль к площадке. Последнее произведение является, по определению, расходом жидкости через площадку,т. е.

.

Припишем величине знаки (-) или (+) в зависимости от направления векторови(противоположные или одноимённые), т.е. втекает жидкость внутрь поверхности (+) или вытекает из неё наружу (-). Если рассматривать однородную несжимаемую жидкость, то объём втекающей внутрь поверхности жидкости за любой промежуток времени равен объёму жидкости, вытекающей из неё. Суммарный расход через поверхность тогда, очевидно, будет равен нулю, т. е.

. (7.1)

Применяя теорему Гаусса-Остроградского к рассматриваемой замкнутой поверхности , получим

. (7.2)

Подставляя (7.1) в (7.2) получим

. (7.3)

Так как поверхность была выбрана произвольно и никаких ограничений сделано не было, то из (7.3) следует, что

(7.4)

в каждой точке объёма .

В декартовой системе координат зависимость (7.4) будет иметь вид

. (7.5)

Уравнение (7.5) представляет собой уравнение неразрывности в дифференциальной форме; оно должно выполняться в каждой точке потока несжимаемой жидкости и накладывает, таким образом, ограничения на компоненты ,ивектора скорости. Заметим для сравнения, что при движении материальной точки (в классической механике) никаких ограничений на её скорость не накладывается, в то время как в любой точке потока несжимаемой жидкости такое ограничение существует в виде уравнения (7.5).

Задача 7.1.Может ли существовать поток несжимаемой жидкости, поле скорости которого описывается векторомс компонентами

,

где – постоянный коэффициент, введённый, в частности, для сохранения размерности скорости?

Решение.В каждой точке потока несжимаемой жидкости обязательно должно выполняться уравнение неразрывности (7.5). Вычислим частные производные

.

Следовательно, в данном случае уравнение неразрывности выполняется в каждой точке и поток с заданными компонентами скорости существует.

8. Общий характер движения жидкой частицы

Жидкость обладает свойством текучести и является легко деформируемой средой, пример – трансформация жидкой капли при растекании её по твёрдой поверхности. Напомним, что твёрдое тело может участвовать одновременно в поступательном движении и во вращательном. Одной из характеристик интенсивности вращательного движения является угловая скорость . Если известно поле скоростей, то возможно определить вектор(ротор вектора скорости), связанный с вектором угловой скороститак

Помимо вращательного движения жидкая частица может деформироваться, и для каждой её точки это будет эквивалентно участию в так называемом деформационном движении. Все возможные виды наглядно изображены на рис. 8.1 и 8.2.

Рис. 8.1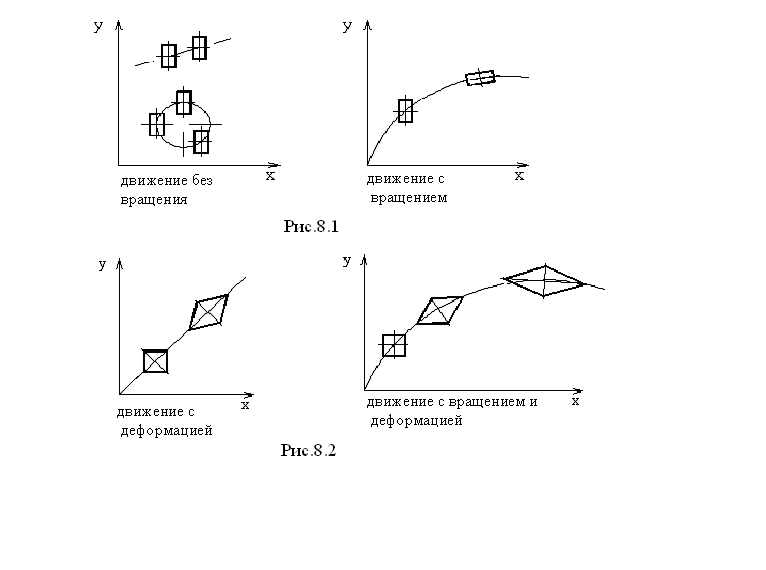

О

Рис. 8.2

сновная теорема кинематики жидкости – первая теорема Коши-Гельмгольца – этот результат формулирует так: скорость любой точки жидкой частицы складывается из скорости полюса, скорости при вращении вокруг мгновенной оси, проходящей через полюс, и скорости деформационного движения. Обозначим составляющие поступательной скорости полюса,и, составляющие вектора угловой скорости полюса,и, составляющие скорости деформации U_xдеф,U_yдефи U_zдеф. Тогда возможно выразить проекции скоростей движения в любой точке потока. Например,

.

Задача 8.1. Выразить проекцию скоростичерез,иU_zдеф.