1. Основные определения. Виды движения

При изучении движения жидкости она считается сплошной средой и её движение происходит потоком. Под потоком понимают движение массы жидкости, ограниченной системой поверхностей твердых тел (трубопровод, канал, река и т. д.). Движение сплошной среды характеризуется, прежде всего, скоростями её частиц, поэтому в дальнейшем в примерах рассматривается скорость .

1.1. Два метода изучения движения жидкости

М

Рис. 1.1

етод Лагранжа. Для удобства исследования любой жидкий объем можно представлять состоящим из большого числа жидких частиц. Если учесть, что «частицы» должны заполнять пространство без промежутков, правильнее было бы сказать, что весь объём движущейся жидкости представляется разделённым воображаемыми перегородками на бесконечное множество объёмов (частиц). В соответствии с этим, когда возникает необходимость к изучению движения жидкой частицы, возможен такой же подход, как и к изучению движения точки в механике. Применяя этот метод, мы должны изучить движение каждой частицы жидкости, указывая её положение в пространстве в любой момент времени, используя ортогональную декартовую систему координат с осями ox, oy, oz. Для этого, прежде всего, необходимо найти способ отличить одну частицу от другой; с этой целью допустим, что в некоторый начальный момент времени t₀ интересующая нас частица находилась в точке с координатами x=a, y=b, z=c (они не меняются со временем). С течением времени, т. е. в последовательные моменты t₁, t₂, … t_n частица изменяет свое положение в пространстве, рис.1.1. Координаты её определяются уравнениями

,,, (1.1)

которые описывают траекторию движения заданной (изучаемой) частицы.

Траекторией называется совокупность точек пространства, через которые движущаяся частица проходит в последовательные моменты времени.

Если известны уравнения (1.1), то скорость и ускорение частицы в любой момент времени находятся дифференцированием по времени и принципиальных затруднений на этом пути нет. При практическом применении метод Лагранжа встречает значительные трудности, так как для изучения всего потока необходимо знать уравнения типа (1.1) для каждой частицы, что на самом деле практически невозможно. Метод Лагранжа сравнительно редко применяется в механике жидкости и газа, например, при изучении волновых движений.

Метод Эйлера. При применении метода Эйлера определяют, какие значения имеют различные параметры потока (скорость, давление, ускорение и т. д.) в каждой точке пространства. Если взять различные точки и фиксировать время , то при этом в пространстве можно получить мгновенную картину распределения скоростей жидкости –векторное поле скоростей. Фактически в каждой точке будет указан вектор скорости той частицы жидкости, которая проходит через эту точку в рассматриваемый момент времени.

Н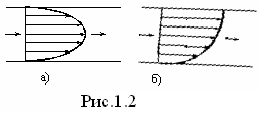а рис. 1.2 приведены примеры распределения скоростей в трубе,рис. 1.2, а и в открытом канале, рис. 1.2, б.

П

а) б)

Рис. 1.2

ри применении метода Эйлера все векторные и скалярные величины рассматриваются как функции координат и времени. Например, скорость в точке может быть представлена в виде вектора

(1.2)

или в виде его проекций на оси декартовой системы

, ,. (1.3)

Принципиальное различие между методом Лагранжа и методом Эйлера состоит в том, что в методе Лагранжа координаты частиц представляются как функции времени, а в методе Эйлера скорости частиц являются функциями координат и времени. Поэтому в методе Эйлера координаты x,y,и z являются независимыми переменными, а в методе Лагранжа они являются зависимыми. В дальнейшем, если не сделано специальных оговорок, применяется метод Эйлера для описания движения жидкости.

Задача 1.1. Выполнить переход от метода Лагранжа к методу Эйлера.

Решение.По методу Лагранжа движение жидкости определяется системой (1.1). Найдём скорости,, и , дифференцируя уравнение (1.1) по времени.

Результат будет таким

, ,.

Для того, чтобы выразить a,bиcчерезx,yиz, система (1.1) решается относительноa,bиcи эти зависимости подставляются в только что полученную дифференцированием по времени систему. В результате напишем уравнения движения в координатахx,y,zиt

, ,.