Сравнения. Кольцо классов вычетов

Множество Z можно разбить на классы чисел сравнимых между собой по модулю m и называемых классами вычетов по модулю m. Каждый класс вычетов имеет вид

,

так что

.

Каждым двум классам и независимо от выбора в них представителей k,l можно сопоставить классы, являющиеся их суммой или произведением, то есть на множестве классов вычетов по модулю m однозначным образом индуцируются операции и :

Так как определения этих операций сводятся к соответствующим операциям над числами из классов вычетов, то есть над элементами из Z, то {Zm,, } будет так же коммутативным кольцом с единицей . Оно называется кольцом классов вычетов по модулю m. Итак мы показали, что конечные кольца существуют. Приведем три примера, указывая отдельно таблицы сложения и умножения:

+	0	1
0	0	1
1	1	1

∙	0	1
0	0	0
1	0	1

+	0	1	2
0	0	1	2
1	1	2	0
2	2	0	1

∙	0	1	2
0	0	0	0
1	0	1	2
2	0	2	1

+	0	1	2	3
0	0	1	2	3
1	1	2	3	0
2	2	3	0	1
3	3	0	1	2

∙	0	1	2	3
0	0	0	0	0
1	0	1	2	3
2	0	2	0	2
3	0	3	2	1

Гомоморфизмы колец

Отображение обладает следующими свойствами:

, .

Это дает нам основания говорить о гомоморфизме Z и Zm.

Определение.

Пусть 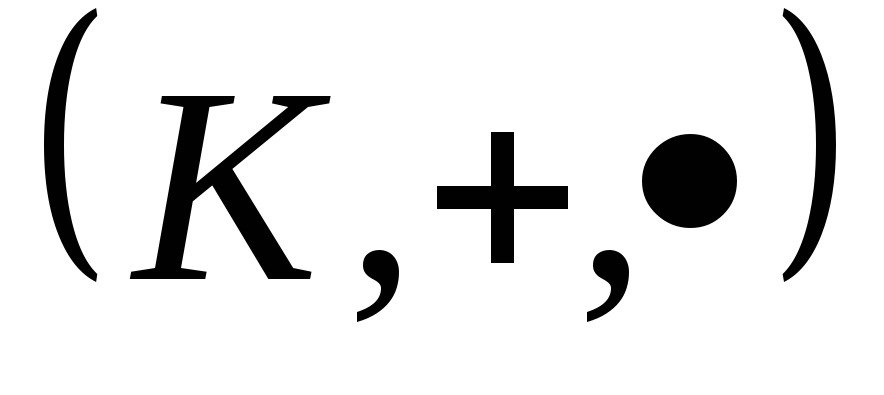и(К',, )– кольца. Отображение f:КК' называется гомоморфизмом, если оно сохраняет все операции, то есть если

,f(b).

При этом, конечно, f(0)=0'и f (na) = nf (a), nZ.

Ядром гомоморфизма f называется множество

.

Ясно, что Кer f - подкольцо в К. Как и в случае групп гомоморфизм f:К в К' называется мономорфизмом, если Кer f = 0. Эпиморфизмом, если образ совпадает сК', то есть

.

Изоморфизмом, если отображение f мономорфно и эпиморфно.

Факт изоморфизма колец кратко записывают в виде . Отображениеявляется эпиморфизмомZ в Z_m с ядром Кer f=mZ. Если рассматривать только кольца с 1, то в определение гомоморфизма f: К К', целесообразно ввести условие .

Типы колец. Поля

В числовых кольцах Z,Q и R из равенства следует, чтоa=0 или b=0. Но кольцо квадратных матриц М_n над любым из указанных колец этим свойством не обладает.

Рассмотрим матрицу , в которой на пересеченииi-ой строки и j-го столбца стоит единица, а все остальные элементы равны 0. Очевидно, что при, хотя . В коммутативном кольце выполнено равенство .

Определение.

Если ab=0 при и в кольце К, то a называется левым, а b правым делителем нуля (в коммутативном кольце говорят просто о делителях 0).

Сам 0 в кольце – тривиальный делитель 0. Если других делителей 0 нет (кроме 0), то К называется кольцом без делителей нуля. Коммутативное кольцо с 1 и без делителей 0 называется целостным кольцом (кольцом целостности или областью целостности).

Теорема 1.

Нетривиальное коммутативное кольцо К с единицей является целостным тогда и только тогда, когда в нем выполнен закон сокращения

ab = ac, a0, bca,b,cK.

В самом деле, если в К имеет место закон сокращения, то из

аb = 0 = а0либо а=0, либо а0, ноb=0.

Обратно: если К область целостности, то

ab = ac, a0a(b - c) = 0 b – c = 0 b = c.

В кольце К с единицей естественно рассматривать множество обратимых элементов. Элемент а называется обратимым или делителем 1, если существует элемент а^-1 для которого ^-1 = 1 = . Точнее следовало бы говорить об элементах обратимых справа или слева (ab=1 или ba=1), но в коммутативных кольцах, а так же в кольцах без делителей нуля, эти понятия совпадают. Действительно, ab=1aba=a, откуда

a(ba-1)=0, так как а0 , то ba-1=0, ba=1.

Например, в кольце М_n обратимый элемент это в точности матрицы с отличным от нуля определителем.

Обратный элемент a не может быть делителем 0

ab=0a^-1(ab)=0(a^-1a)b=0b=0(аналогично ba=0b=0).

Теорема 2.

Все обратимые элементы кольца Кс единицей составляют группу V(К)

по умножению.

Доказательство.

В самом деле, так как множество V(К) содержит 1, аV(К)а^-1V(К) и ассоциативность по умножению в К выполнена, то надо только убедиться в замкнутости множества V(К), то есть проверить, что произведение аb любых элементов a и b из V(К) будет снова принадлежать V(К), но это очевидно, так как

аb- обратим.

Легко видеть, что - циклическая группа порядка 2.

Мы получили интересный класс колец, так называемое кольцо с делением или тела. Заметив, в определении кольца аксиому К2) на существенно более сильные условия К2') относительно операции умножения множество К\является группой. Кольцо с делением всегда без делителей нуля и каждый не нулевой элемент в нем обратим .

Операции «+» и «» становятся почти полностью симметричными в коммутативном кольце с делением, которое называется полем.

Определение.

Поле Р – это коммутативное кольцо с единицей (10) в котором каждый элемент обратима0.

Группа Р*=V(Р) называется мультипликативной группой поля. Поле представляет собой гибрид двух абелевых групп: аддитивной и мультипликативной, связанных законом дистрибутивности. Теперь уже одним в виду коммутативности. Подполем F поля Р называется подкольцо в Р. Само являющееся полем, например: поле рациональных чисел Q- подполем поля вещественных чисел R. В случае FP говорят также, что поле Р является расширением своего подполя F, из определения подполя следует, что нуль и единица поля Р будут содержаться в F и служить для F нулем и единицей. Говорят, что расширение F₁ поля F получено присоединением к F элемента а и отражают это записью f₁=f(a). Аналогично можно говорить о подполе F₁=F(a₁,…,a_n) поля Р, полученном присоединением к F элемента а и отражают это записью F₁=F(a). Аналогично можно говорить о подполе F₁=F(a₁,…,a_n) поле Р, полученном присоединением к F n элементов (a₁,…,a_n). Проверка показывает, что Q() совпадает с множеством чисела+b, где а,bQ так как ()²=2 и

.

При a+b то же самое относится к Q(),Q и так далее.