Группоиды и полугруппы

1) В зависимости от числа операций, определенного в данном множестве, в зависимости от свойств этих операций, общая алгебра подразделяется на отдельные части. Самым простым алгебраическим образованием является множество с одной алгебраической операцией, на которую не налагается никаких условий. Называется оно группоидом. Если на алгебраическую операцию наложить некоторые условия, например, предположить, что операция коммутативна, то такие группоиды называются коммутативными или абелевыми ( в честь великого норвежского математика 19 века Н.Г. Абеля).

Определение.

Группоиды с ассоциативной операцией называются полугруппами.

Теория полугрупп является одной из наиболее содержательных областей общей алгебры. Если полугруппа содержит единичный элемент , то она называется полугруппой с единицей, ее единичный элемент называется единицей полугруппы. Примером полугруппы является множество, N₀ по отношению к сложению, а так же по отношению к умножению.(N₀ = N 0).

Группы

Определение 1.

Полугруппа G с единицей е называется группой, если для каждого ее элемента а существует такой элемент а'G, что

аа' = а'а = е. ( 1)

Будем с этого момента алгебраическую операцию в группе называть умножением и обозначать символом обычного умножения, ее результат будем называть произведением. Элемент а' из (1) назовем обратным к а и обозначим символом а^-1. Таким образом (1) запишется так:

аа^-1 = а^-1а = е. (1')

Определение 2.

Группа – это множество замкнутое относительно одной ассоциативной алгебраической операции, содержащее единичный элемент и такой, что для каждого ее элемента а существует обратный элемент, который удовлетворяет равенству (1').

Отметим некоторые простейшие свойства групп.

1. Всякий элемент группы имеет только один обратный.

2. (а^-1)^-1 = а.

3. (ab)^-1 = b^-1a^-1.

4. ( а₁а₂ … а_n )^-1 = а_n^-1а_n-1^-1… а₂^-1а₁^-1.

Докажем, например, свойство 3.

Пользуясь, ассоциативностью умножения в группе, получаем

(ab)(b^-1a^-1) = a(bb^-1)a^-1 = aea^-1 = aa^-1=e.

Это означает, что обратным к элементу аb является b^-1 а^-1.

В группе однозначно, разрешимы уравнения

ах = b, уа = b. (2)

Это означает, что для каждой пары а и b существует одна и только одна пара элементов х и у, удовлетворяющих равенствам (2). Заметим, что если в полугруппе G для каждой пары элементов a,b G разрешимы уравнения (2), то G является группой, то есть в G существует единица и каждый элемент имеет обратный. Итак, группу можно определить как группоид с ассоциативным умножением, в котором для каждой пары элементов а и b разрешимы уравнения (2).

Определение.

Группа называется абелевой, если умножение в ней коммутативно.

Для обозначения алгебраической операции в абелевых группах принято употреблять символ +, операцию эту называют сложением, единичный элемент обозначают символом 0 и называют нулем, элемент обратный к а обозначается через –а. В связи с этим говорится о двух терминологиях в теории групп: мультипликативной, связанной с термином умножение для обозначения групповой операции и употребляемой в неабелевых группах и в общей теории групп и о терминологии аддитивной, связанной с термином сложения для обозначения групповой операции и употребляемой обычно в абелевых группах. Аддитивная (сложение) используется для обозначения групповой операции, употребляемых обычно в абелевых группах.

В группе справедлив закон сокращения: из ab = ac b = c и из

ba = ca b = c.

Группа, состоящая из конечного числа элементов, называется конечной, а число ее элементов – порядком группы. Можно доказать, что для того чтобы конечная полугруппа была группой, достаточно, чтобы в ней выполнялся закон сокращения. Рассмотрим примеры групп:

1) Каждое из множеств: Z, Q, R, C, рассматриваемое со сложением, в качестве операции образует группу; это соответственно: группа аддитивная целых рациональных, действительных и комплексных чисел. Единичным элементом каждой из этих групп является число 0. Элементом обратным к а является число –а, все они абелевы, бесконечны. Группу относительно сложения образуют так же все четные числа, а не нечетные – не образуют группы по сложению.

2) Множества Q, R, C каждое взятое без нуля образуют группы по отношению к умножению чисел. Те же множества с нулем не являются группами по отношению к умножению (нуль не имеет обратного элемента). Все эти группы абелевы и бесконечны. Единицей в каждой из них является число 1, обратным к числу а является 1/a.

3) Число 0 образует группу относительно сложения чисел. Число 1 является группой по отношению умножения. Обе они конечные, порядка 1, абелевы.

4) Числа 1 и -1 с умножением в качестве алгебраической операции образуют абелевую группу второго порядка.

Абелевой группой является так же множество {1, -1, i, -i}, если в качестве операции рассматривать умножение комплексных чисел. Вообще множество корней n степени из 1 являются группой, если в качестве операции рассматривать их умножение.

5) Группа, заданная таблицей называется группой Клейна четвертого порядка (Ф.Клейн выдающийся немецкий математик второй половины 19 и начала 20 века).

Таблица 1.

	е	а	b	c
e	e	a	b	c
a	a	e	c	b
b	b	c	e	a
c	c	b	a	e

Она абелева и в ней каждый элемент обратен себе.

Можно показать, что множество всех взаимнооднозначных отображений, некоторого множества на себя является группой относительно их суперпозиции. Если, в частности, Х является конечным множеством, то его взаимнооднозначные отображения на себя называются подстановками.

Пусть Х состоит из n элементов так как их природа не играет никакой роли, можно считать, что этими элементами считаются числа 1, 2, … , n. Тогда некоторую подстановку σ множества Х удобно представить в форме:

σ = , (3)

где в верхнем ряду записаны элементы множества Х не (обязательно в их естественном порядке), а в нижнем - образы соответствующих элементов. Например

, (4)

представляет собой некоторую подстановку множества, состоящего из шести элементов. Единицей группы является тождественная подстановка

.

Подстановкой обратной к (3), будет

.

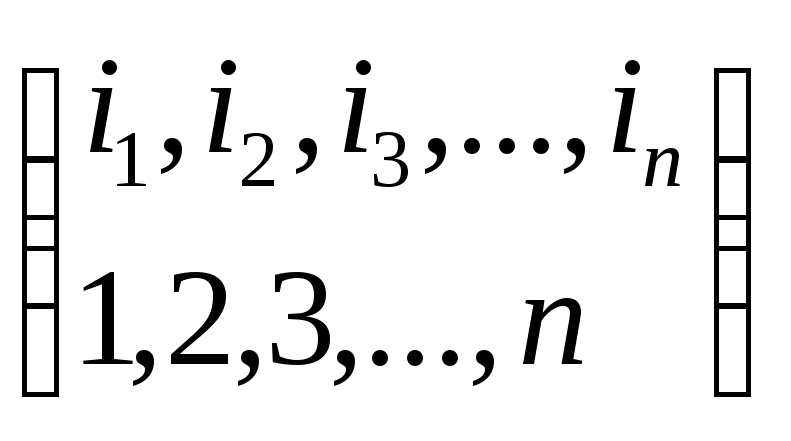В частности, для подстановки (4) обратной будет

= .

Следующий пример иллюстрирует способ умножения подстановок:

=.

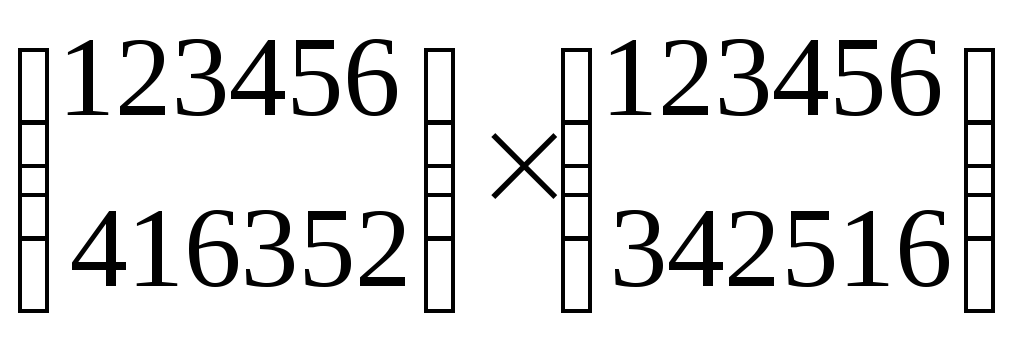Первая подстановка переводит 1 в 4, вторая 4 в 5 итак в результате их обеих 1 переходит в 5. Аналогично 2 в1, потом окончательно 1 переходит в 3 и так далее.

Определение.

Группа всех подстановок множества, состоящего из n элементов, называется симметрической группой n-й степени. Она состоит из n! элементов, так как множество из n элементов можно упорядочить n! различными способами.

Умножая, теперь подстановки из нашего примера в обратном порядке, получим

,

откуда видно, что умножение подстановок некоммутативно.

Множество R со сложением в качестве алгебраической операции является группой. Но Q, будучи подмножеством R само является группой по отношению к той же самой операции. Об аддитивной группе рациональных чисел говорим поэтому, что она является подгруппой аддитивной группы действительных чисел. Вообще, не пустое подмножество Н группы G называется ее подгруппой, если Н само является группой по отношению к алгебраической операции в G. Каждая группа содержит в качестве подгруппы саму себя и подгруппу состоящую из одного элемента – единицы группы. Эти подгруппы называются несобственными, всякая другая – собственной.

Пример №1.

Рассмотрим множество Т, состоящее из трех чисел 0, 1, 2. В качестве алгебраической операции в Т возьмем так называемое сложение по модулю 3, заключающееся в том, что если a и bТ, то результатом действия над ними является остаток от деления обычной суммы a+b на 3. Как и в других случаях, когда операция определена на конечном множестве можно представить ее в виде таблицы 2, называемой таблицей Кэли (в честь выдающегося английского математика 19 века Артура Кэли).

Таблица 2. Таблица 3.

	0	1	2
0	0	0	0
1	0	1	2
2	0	2	1

	0	1	2
0	0	1	2
1	1	2	0
2	2	0	1

Аналогично определяется умножение по модулю 3 на множестве Т (см. таблицу 3).

Пример №2.

Пусть дан равносторонний треугольник АВС с центром в точке О.

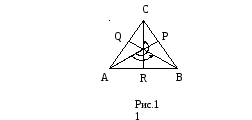
Будем рассматривать вращение треугольника АВС вокруг точки О, совмещающее треугольник АВС с собой (см. рис.1). Будем при этом отождествлять вращение, отличающееся на угол 2πk, k Z.

Таким образом, получим три разных вращения: α₀, α₁, α₁,. α₀ – на углы соответственно 0, 2/3π, 4/3π. Рассматривая множество { α₀, α₁, α₂} с суперпозицией вращения в качестве алгебраической операции, получим группу – группу вращений равностороннего треугольника. Ее таблицей Кэли является следующая таблица.

Таблица 4.

	α0	α1	α2
α0	α0	α1	α2
α1	α1	α2	α0
α2	α2	α0	α1

Но кроме вращений еще возможны и другие самосовмещения треугольника АВС, а именно его симметрии относительно осей АР, ВQ, СR.

Обозначая их соответственно α₃, α₄, α₅ , получим группу вращений и осевых симметрий равностороннего треугольника. Таблицей Кэли, которой является таблица 5.

Таблица 5.

	α0	α1	α2	α3	α4	α5
α0	α0	α1	α2	α3	α4	α5
α1	α1	α2	α0	α4	α5	α3
α2	α2	α0	α1	α5	α3	α4
α3	α3	α5	α4	α0	α2	α1
α4	α4	α3	α5	α1	α0	α2
α5	α5	α4	α3	α2	α1	α0

Группа вращений равностороннего треугольника является ее подгруппой. Одни симметрии совместное с тождественным отображением не образуют группы.

Сравним две таблицы 2 и 4. Обе они являются таблицами Кэли некоторых групп, каждая из которых состоит из трех элементов. По конкретному характеру своих элементов эти группы совершенно различны. Одна из них - группа чисел 0, 1, 2 со сложением по модулю 3, другая – группа вращений равностороннего треугольника. Если абстрагироваться от конкретного содержания их элементов, замети, что эти таблицы, а значит, и соответственные группы не отличаются одна от другой. Они алгебраически в некотором смысле тождественны. Если мы из таблицы 4 устраним букву α , оставляя только индекс, то эти таблицы вообще ничем не будут отличаться. Это соответствует тому, что мы соответствующие вращения обозначим символами 0, 1, 2. Но ведь мы можем обозначить вращение, как нам захочется. Короче говоря, алгебраическое строение этих групп идентично.

Определение.

Группы G и G' называются изоморфными, если между их элементами можно установить такое взаимнооднозначное соответствие, что если аа' иb b', где а, b G ,а' ,b'G', то abа' b'.

Поскольку в силу взаимно однозначного соответствия ab(ab)', то изоморфизм двух групп G и G' можно определить еще как такое взаимно однозначное соответствие между их элементами при котором (ab)'=a'b', то есть при котором образ произведения двух элементов равняется произведению их образов. Можно доказать, что при изоморфизме групп единица переходит в единицу и что

(а^-1)' = (а')^-1 , то есть образ обратного элемента равен обратному к его образу.

Примеры изоморфизма групп.

1. Мультипликативная группа корней третий степени из единицы изоморфна группе вращений равностороннего треугольника, а значит и группе множества {0,1,2} со сложением по модулю 3. Заметим, что свойство изоморфизма рефлексивно, симметрично и транзитивно. Вообще мультипликативная группа корней из единицы при произвольном n изоморфна группе вращений правильного n – угольника и группе чисел 0, 1,…,n-1 со сложением по модулю n.

2. Мультипликативная группа положительных действительных чисел изоморфна аддитивной группе всех действительных чисел. Взаимно однозначное соответствие между этими группами установим ток, что каждому действительному положительному числу х поставим в соответствие его логарифм при основании, например, 10. Тогда если х' = lg x и у' = lg у, то (ху)' = lg ху = lg х + lg у = х' + у', так что это соответствие действительно является изоморфизмом.

Можно доказать, что всякая группа изоморфна группе взаимно однозначных отображений некоторого множества на себя.

Теорема Кели: всякая конечная группа порядка и изоморфна некоторой подгруппе симметрической группы степени n (в частности всей симметрической группе степени n).