Некоторые числовые функции

1. Функция y=[x].

Эта функция называется целой частью от x. Она определена для всех действительных чисел x и представляет собой наибольшее целое число не превосходящее x.

Пример 1.

[8]=8.

Пример 2.

[2,8]=[2].

Пример 3.

[-4,75]=-5.

Построим график функции y=[x]. Если m – целое число, причем m≤x<m+1, то по определению [x]=m. Поэтому график функции имеет вид

Если x целое число, то целая часть равна x и точки графика лежат на прямой y=x.

,

,

и так далее

Видим, что график состоит из ряда отдельных горизонтальных отрезков лишенных правых концов.

Это обстоятельство символизируется стрелками, которые своими остриями указывают на точки не принадлежащие графику функции y=[x].

2. Функция y={x}.

Здесь {x}=x-[x]. Эта функция называется дробной частью от x. Она как и функция y=[x] определена для всех действительных x.

Пример.

{8}=8-[8]=0;

{2.8}=2.8-[2.8]=2.8-2=0.8;

{-4.75}=-4.75-[-4.75]=-4.75-(-5)=0.25.

Лемма 1.

, где x – действительное число, n – натуральное число.

Доказательство.

Пусть целая часть

, то ,.

Отсюда , но. Значит .

Лемма 2.

[2λ]-2[λ]≤1, λ – действительное число.

Доказательство.

λ=[λ]+{λ} |∙2;

2λ-2[λ]=2{λ}. Так как [2λ] ≤2λ, то

[2λ]-2[λ] ≤2{λ}<2;

[2λ]-2[λ] < 2. Отсюда [2λ]-2[λ]≤1. Что и требовалось доказать.

Обозначения. Пусть мы имеем n! и пусть ,, ноне делитn!, то говорят, что p входит в степени r в n!.

Теорема.

, где l – наибольшее такое, что .

Доказательство.

1) n!=1∙2∙3…p…2∙p…3∙p…kp…n.

Выпишем произведение чисел кратных p,

p∙2p∙3p∙…∙kp = .

а все остальные числа не содержат p.

kp≤n, k≤ ,

k – наибольшее целое не превосходящее . Значит .

2) Повторим рассуждения с k! Тогда выделится , но

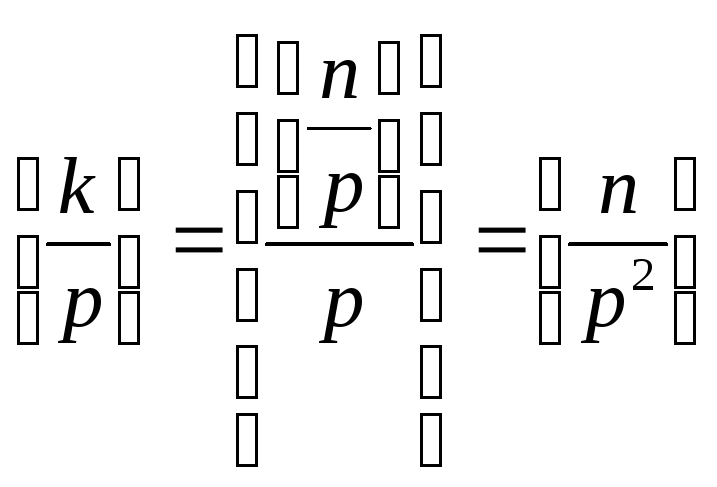
и так далее продолжим наши рассуждения до .

Далее будут 0, так как

.

Итак,

.

Пример.

Доказать, что

Решение.

n=50, p=3.

Найдем показатель r, с которым простое p=3 входит в 50!. По формуле имеем

, то есть.

Функция Эйлера

Функция Эйлера определяется для всех целых положительныхa и представляет собой число чисел

0, 1, …, a-1 (1)

взаимно простых с a.

Примеры: ,,,,,.

Определение.

Функция называетсямультипликативной, если выполнены следующие условия:

1. Функция определена для всех целых положительныхa и не обращается в нуль хотя бы при одном таком a;

2. Для любых положительных взаимно простых иимеем.

Теорема.

Функция Эйлера является мультипликативной. То есть при,, где.

Сумма и число делителей натурального числа

Пусть каноническое (простейшее) разложение числа a. Сумма натуральных делителей S(a) числа a находится по формуле

.

Число делителей τ(а) числа a находится по формуле

.

Функция Мёбиуса.

Функция Мёбиуса определяется для всех положительных целых a. Она задается равенством: , еслиa делится на квадрат числа отличный от единицы; , еслиa не делится на квадрат числа отличный от 1, при этом k обозначает число простых делителей числа a. В частности, при a=1 считаем, что k=0, поэтому принимаем .

Примеры:

, , , ,

, , , ,

, , , .

Задание на дом.

1. Найти показатель с которым 5 входит в каноническое разложение 5258!.

2. Найти τ(5600) и S(5600).

3. Составить таблицу значений 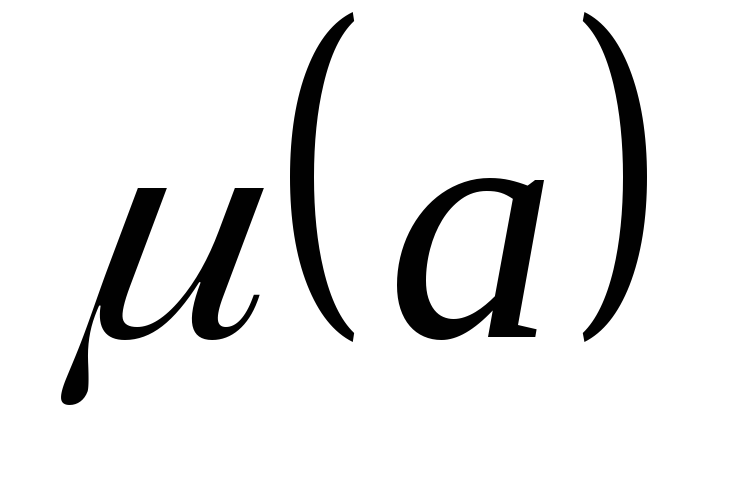для всехa = 1,…,100.

4. Найти и.

5. Решить уравнение .

6. Решить уравнение .

7. Решить уравнение .