3.10. Электрическая цепь с активным сопротивлением
Постоянный ток, проходя по проводнику длиной l, распределяется равномерно по всему сечению S проводника. Сопротивление постоянному току, называемое омическим сопротивлением,
,
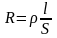(3.24)
где удельное сопротивление материала проводника.
П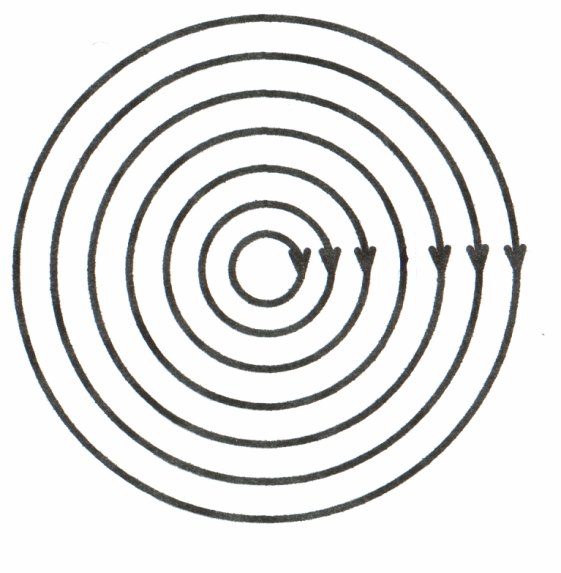
еременный
ток создаёт вокруг проводника и внутри
его переменное магнитное поле (рис.
3.14), которое наводит в каждом элементарном
сечении проводника ЭДС самоиндукции
еL,
препятствующую изменению тока, т. е.
оказывающую переменному току
сопротивление. Потокосцепление
самоиндукции
элементарных сечений, расположенных ближе к центру проводника, больше, чем потокосцепление сечений у поверхности проводника. Поэтому ЭДС самоиндукции в центре проводника будет максимальной, и по мере приближения к поверхности проводника ЭДС будет
Рис. 3.14 уменьшаться. Поэтому ЭДС
самоиндукции будет оказывать
переменному току максимальное противодействие в центре проводника и минимальное – у поверхности проводника. В результате этого плотность тока максимальная у поверхности, минимальная – в центре проводника, т. е. переменный ток в результате противодействия ЭДС самоиндукции вытесняется из внутренних сечений проводника на его поверхность. Это явление называется поверхностным эффектом. В связи с вытеснением переменного тока на поверхность проводника внутренние элементарные сечения проводника не используются (их можно удалить, образовав трубчатый проводник). При этом активное сечение провода уменьшится S S . Тогда сопротивление проводника переменному току
,
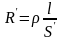(3.25)
называется активным сопротивлением.
Таким образом, активное сопротивление, т. е. сопротивление переменному току больше омического сопротивления, т. е. сопротивления постоянному току.
Поверхностный эффект проявляется тем сильней, чем больше частота переменного тока, площадь поперечного сечения провода, его удельная проводимость и магнитная проницаемость.
При частоте f = 50 Гц и небольшом диаметре медных или алюминиевых проводов активное сопротивление принимается равным омическому.
Рассмотрим электрическую цепь с активным сопротивлением R (рис. 3.15), к которой приложено синусоидальное напряжение
.
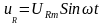(3.26)
Мгновенное значение тока определим по закону Ома:
,
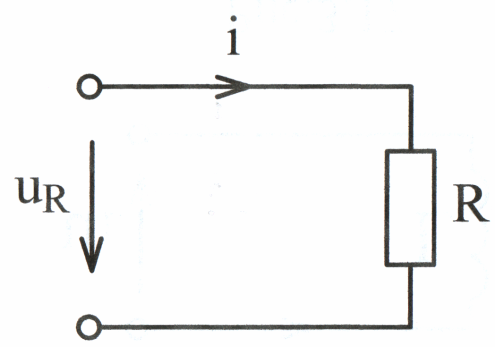
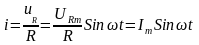(3.27)
где
.
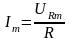(3.28)
Разделив левую и правую части равенства (3.28) на получим действующее значение тока:
Рис.
3.15
.
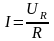(3.29)
Таким образом, для цепи с активным сопротивлением закон Ома справедлив для максимальных и действующих значений тока и напряжения. Сравнивая выражения для мгновенных значений напряжения (3.26) и тока (3.27), видим, что напряжение и ток имеют одинаковую фазу, т. е. угол сдвига фаз
.
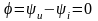(3.30)
Следовательно, в цепи с активным сопротивлением напряжение и ток совпадают по фазе, что отражено на волновой и векторной диаграммах (рис. 3.16).
Цепи переменного тока характеризуются мгновенной мощностью, равной произведению мгновенных напряжений и тока:
.
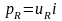(3.31)
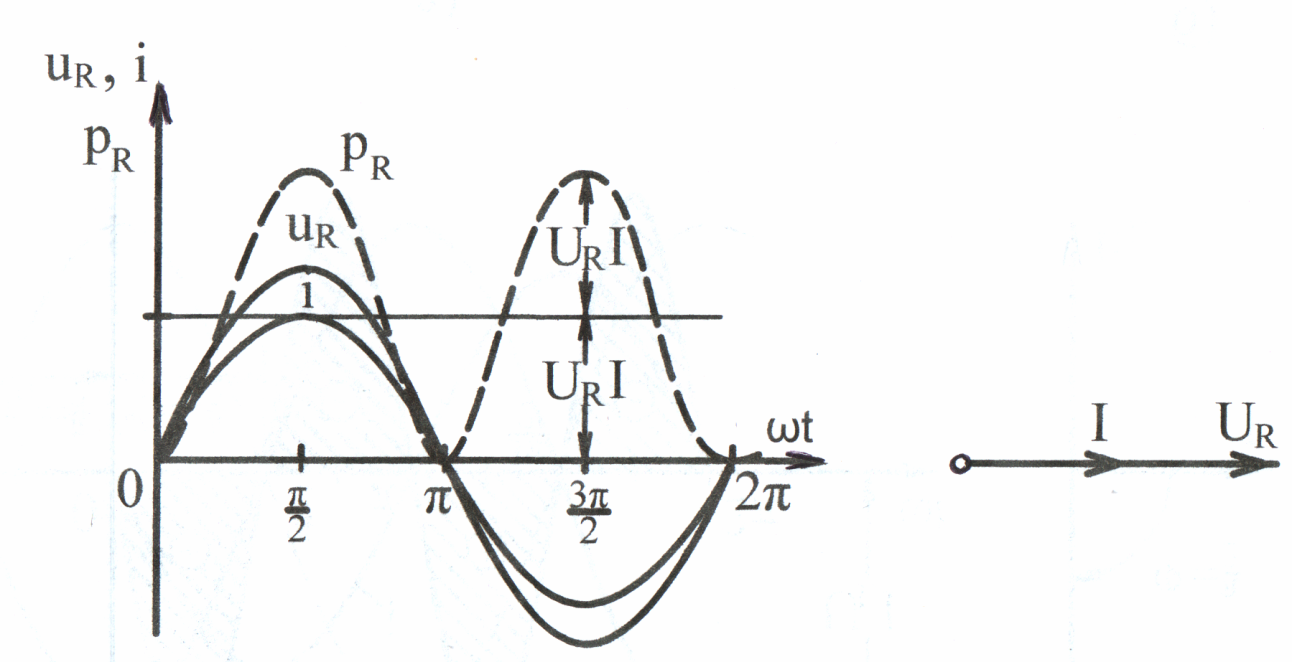
а) б)
Рис. 3.16
Подставив в формулу (3.31) выражения мгновенных напряжения (3.26) и тока (3.27), получим:
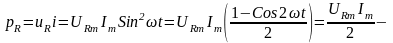
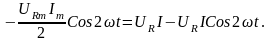(3.32)
Из
(3.32) следует, что мгновенная мощность
имеет постоянную составляющую
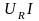и переменную составляющую, которая
изменяется с двойной частотой (рис.
3.16, а ).
Среднее значение мощности за период называется активной мощностью:
.
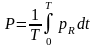(3.33)
Подставив в (3.33) выражение мгновенной мощности (3.32), получим:
.
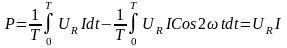При вычислении активной мощности P учтено, что второй интеграл равен нулю. Таким образом, активная мощность цепи с сопротивлением R
.
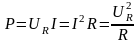(3.34)
Единица измерения активной мощности – ватт [Вт].