
- •Глава 3. Однофазные электрические цепи синусоидального тока
- •Периодические переменные эдс, напряжения и токи
- •3.2. Явление электромагнитной индукции
- •3.3. Явление самоиндукции и эдс самоиндукции. Индуктивность
- •3.4. Источник синусоидальной эдс
- •3.5. Волновые диаграммы токов и напряжений
- •3.6. Действующее и среднее значения синусоидального тока
- •3.7. Изображение синусоидальных эдс, напряжений и токов вращающимися векторами
- •3.8. Законы Кирхгофа для электрической цепи синусоидального тока
- •3.9. Особенности электрических цепей переменного тока
- •3.10. Электрическая цепь с активным сопротивлением
- •3.11. Электрическая цепь с индуктивностью
- •Электрическая цепь с ёмкостью
- •3.13. Электрическая цепь с последовательным соединением сопротивления, индуктивности и ёмкости
- •3.14. Резонанс напряжений
- •2. Расчёт цепи при резонансе напряжений.
- •3.15. Эквивалентные схемы пассивных двухполюсников переменного тока
- •3.16. Электрическая цепь с параллельным соединением приёмников
- •3.17. Резонанс токов
- •3.18. Компенсация сдвига фаз
- •3.18. Комплексный метод расчёта цепей синусоидального тока
- •3.18.1. Общие сведения о комплексных числах
- •3.18.2. Изображение синусоидальных напряжений и токов комплексными числами
- •3.18.3. Закон Ома в комплексной форме
- •3.18.4. Комплексное сопротивление и комплексная проводимость
- •3.18.5. Законы Кирхгофа в комплексной форме
- •3.18.6. Определение мощности по комплексным напряжению и току
- •3.18.7. Применение методов расчёта цепей постоянного тока к расчёту цепей синусоидального тока
- •1. Классический метод.
- •2. Символический (комплексный) метод.
- •Важнейших открытий XIX века, заложивших фундамент «Теоретических основ электротехники»
- •Важнейших изобретений XIX, начала XX века в области электротехники
- •3.2. Явление электромагнитной индукции __________________________ 75
- •Часть 1. Линейные и нелинейные электрические цепи постоянного тока. Однофазные цепи синусоидального тока.
3.3. Явление самоиндукции и эдс самоиндукции. Индуктивность
Явление наведения ЭДС в каком-либо контуре (рис. 3.3) при изменении тока, протекающего по этому же контуру, называется самоиндукцией. Наведённая (индуктированная) ЭДС
н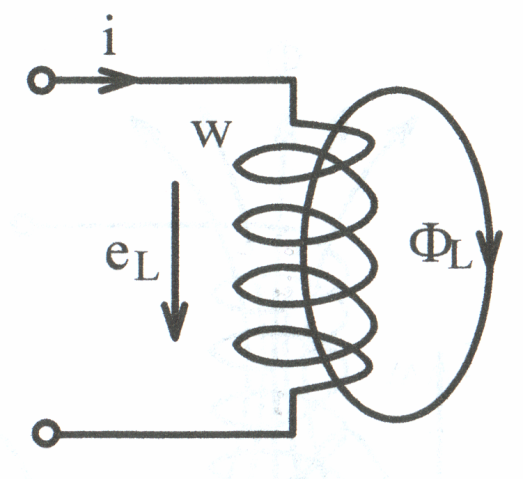 азывается
ЭДС
самоиндукции (
азывается
ЭДС
самоиндукции (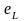 ).
Для определения её в соответствии с
законом электромагнитной индукции
(3.1) надо продиффи-ринцировать
потокосцепление контура
).
Для определения её в соответствии с
законом электромагнитной индукции
(3.1) надо продиффи-ринцировать
потокосцепление контура
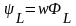 ,
вызванное
,
вызванное
собственным током i, т. е.
Рис.
3.3
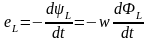 ,
(3.3)
,
(3.3)
где ФL – магнитный поток
самоиндукции.
Из опыта известно, что для контуров (катушек) с неферромагнитным сердечником или для катушек с сердечником из магнитодиэлектриков, у которых магнитная проницаемость не зависит от напряжённости магнитного поля, потокосцепление самоиндукции L прямо пропорционально току i, т. е.
L = L i. (3.4)
Коэффициент пропорциональности L между L и i (коэффициент самоиндукции) называется собственной индуктивностью контура или индуктивностью. Индуктивность катушки зависит от геометрических размеров катушки и числа её витков, но не зависит от величины тока, протекающего по катушке. Единица измерения L – генри Гн] = [Омс].
Учитывая выражения (3.3) и (3.4) имеем:
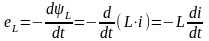 .
(3.5)
.
(3.5)
Таким образом, ЭДС самоиндукции в катушке прямо пропорциональна скорости изменения тока в этой катушке.
П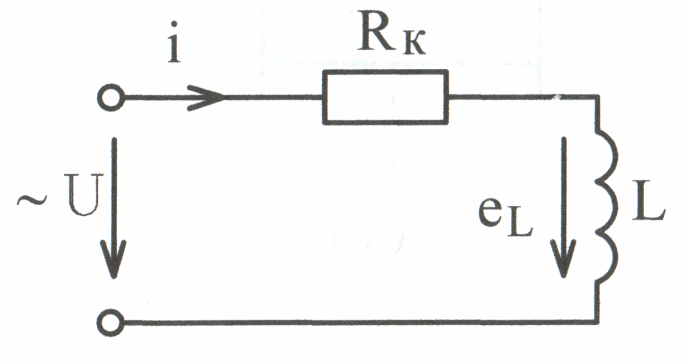 оложительное
направление ЭДС самоиндукции еL
совпадает с положительным направлением
тока i
(рис. 3.3). Знак «
» в формуле (3.5) свидетельствует о том,
что мгновенное значение ЭДС самоиндукции
отрица-
оложительное
направление ЭДС самоиндукции еL
совпадает с положительным направлением
тока i
(рис. 3.3). Знак «
» в формуле (3.5) свидетельствует о том,
что мгновенное значение ЭДС самоиндукции
отрица-
Рис. 3.4 тельно, если приращение
тока
положительно (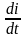
0), т. е. ЭДС самоиндукции катушки
препятствует изменению тока в ней
(оказывает сопротивление переменному
току).
0), т. е. ЭДС самоиндукции катушки
препятствует изменению тока в ней
(оказывает сопротивление переменному
току).
Реальную катушку (рис. 3.3) при переменном токе можно заменить эквивалентной схемой (рис. 3.4) с параметрами Rк и L.
Сопротивление катушки Rк характеризует преобразование
 электрической
энергии в
тепловую.
электрической
энергии в
тепловую.
Индуктивность катушки характеризует возникновение в ней ЭДС самоиндукции при протекании по катушке переменного тока i.
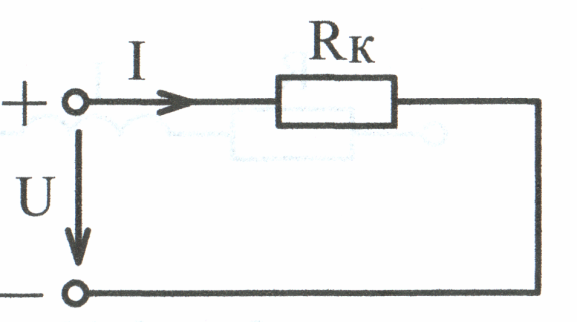
Рис. 3.5 В цепи постоянного тока I
катушка характеризуется только
одним
параметром Rк
(рис.
3.5), так как в этом случае ЭДС самоиндукции
равна нулю (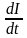 =
0).
=
0).
3.4. Источник синусоидальной эдс
Для получения синусоидальных токов в линейных цепях ЭДС также должны изменяться по синусоидальному закону. Простейшим источником синусоидальной ЭДС может служить прямоугольная рамка с w витками, равномерно вращающаяся в однородном магнитном поле вокруг оси, перпендикулярной к направлению линий магнитной индукции (рис. 3.6).
В результате изменения магнитного потока, пронизывающего рамку, в ней по закону электромагнитной индукции индуктируется ЭДС.
Пусть в момент вращения t = 0 плоскость рамки перпендикулярна линиям магнитной индукции (рис. 3.6, б); тогда магнитный поток, пронизывающий рамку Ф будет иметь
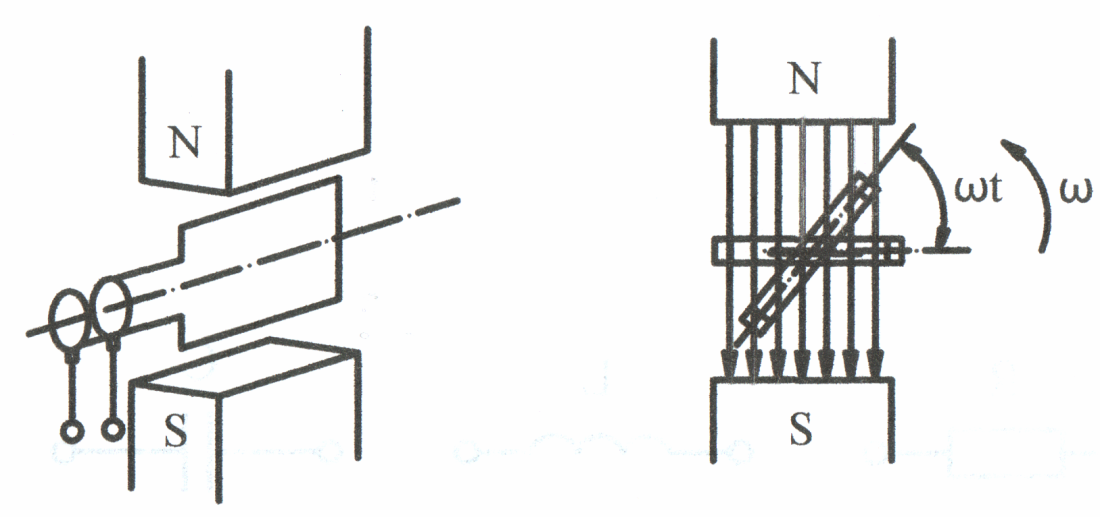
а) б)
Рис. 3.6
максимальное значение Фm. Если угловая скорость вращения
рамки, то в момент времени t рамка повернётся на угол t и мгновенное значение потокосцепления рамки с w витками
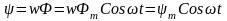 ,
(3.6)
,
(3.6)
где m = wФm – максимальное значение потокосцепления рамки.
Мгновенное значение ЭДС рамки определим по закону электромагнитной индукции:
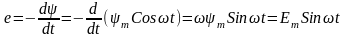 ,
(3.7)
,
(3.7)
г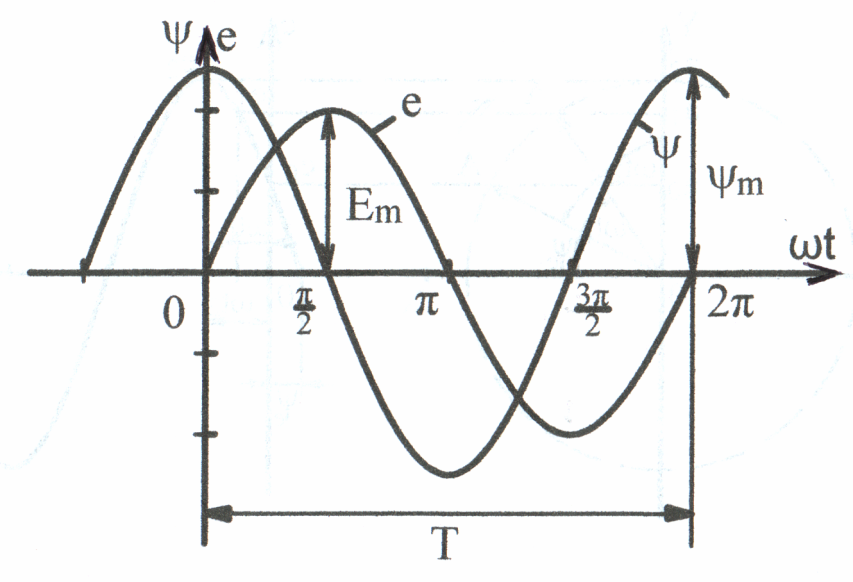 де
де
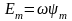
(3.8)
(3.8)
максимальное значение ЭДС, наведённой в рамке.
Из выражения (3.7) видно, что ЭДС, индуктируемая в рамке, изменяется по синусо-идальному закону.
Построим зависимость
Рис. 3.7 мгновенных значений
потокосцепления и ЭДС от угла t, зависящего от времени, используя выражения (3.6) и (3.7) рис. 3.7. Кривые изменения , е во времени называются временной (волновой) диаграммой.
Из временной диаграммы видно, что ЭДС достигает максимального значения Еm в момент времени, когда потокосцепление рамки равно нулю, а скорость изменения потокосцепления ( ) достигает наибольшего значения; ЭДС равна нулю в момент времени, когда потокосцепление рамки имеет максимальное значение m, а = 0.
Из графика рис. 3.7 следует, что при повороте рамки на 360, угол t равен
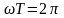 ,
,
откуда
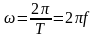 .
(3.9)
.
(3.9)
Величина
,
пропорциональная частоте f,
называется угловой
частотой
ЭДС (тока, напряжения). Единица измерения
,
в отличие от единицы измерения частоты
f,
совпадает с размерностью [
]
=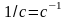 .
.
Генераторы переменного тока по принципу действия не отличаются от рассмотренного устройства (рис. 3.6), но имеют более сложную конструкцию.
