
- •Глава 3. Однофазные электрические цепи синусоидального тока
- •Периодические переменные эдс, напряжения и токи
- •3.2. Явление электромагнитной индукции
- •3.3. Явление самоиндукции и эдс самоиндукции. Индуктивность
- •3.4. Источник синусоидальной эдс
- •3.5. Волновые диаграммы токов и напряжений
- •3.6. Действующее и среднее значения синусоидального тока
- •3.7. Изображение синусоидальных эдс, напряжений и токов вращающимися векторами
- •3.8. Законы Кирхгофа для электрической цепи синусоидального тока
- •3.9. Особенности электрических цепей переменного тока
- •3.10. Электрическая цепь с активным сопротивлением
- •3.11. Электрическая цепь с индуктивностью
- •Электрическая цепь с ёмкостью
- •3.13. Электрическая цепь с последовательным соединением сопротивления, индуктивности и ёмкости
- •3.14. Резонанс напряжений
- •2. Расчёт цепи при резонансе напряжений.
- •3.15. Эквивалентные схемы пассивных двухполюсников переменного тока
- •3.16. Электрическая цепь с параллельным соединением приёмников
- •3.17. Резонанс токов
- •3.18. Компенсация сдвига фаз
- •3.18. Комплексный метод расчёта цепей синусоидального тока
- •3.18.1. Общие сведения о комплексных числах
- •3.18.2. Изображение синусоидальных напряжений и токов комплексными числами
- •3.18.3. Закон Ома в комплексной форме
- •3.18.4. Комплексное сопротивление и комплексная проводимость
- •3.18.5. Законы Кирхгофа в комплексной форме
- •3.18.6. Определение мощности по комплексным напряжению и току
- •3.18.7. Применение методов расчёта цепей постоянного тока к расчёту цепей синусоидального тока
- •1. Классический метод.
- •2. Символический (комплексный) метод.
- •Важнейших открытий XIX века, заложивших фундамент «Теоретических основ электротехники»
- •Важнейших изобретений XIX, начала XX века в области электротехники
- •3.2. Явление электромагнитной индукции __________________________ 75
- •Часть 1. Линейные и нелинейные электрические цепи постоянного тока. Однофазные цепи синусоидального тока.
3.18.5. Законы Кирхгофа в комплексной форме
Первый закон Кирхгофа – алгебраическая сумма комплексных токов в узле электрической цепи равна нулю:
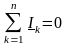 .
(3.140)
.
(3.140)
Второй закон Кирхгофа – в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура:
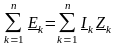 .
(3.141)
.
(3.141)
При составлении уравнений по законам Кирхгофа в комплексной форме необходимо указать на схеме электрической цепи условное положительное направление всех ЭДС и токов, а также направление обхода по независимым контурам. Знак слагаемых в уравнениях определяется так же, как в цепях постоянного тока.
3.18.6. Определение мощности по комплексным напряжению и току
Непосредственное
применение комплексного метода к
вычислению мощности невозможно. Однако
для вычисления активной, реактивной и
полной мощности по символическим
изображениям напряжения и тока может
быть использован искусственный приём.
Для этого комплексное
напряжение
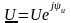 необходимо умножить на комплекс тока
необходимо умножить на комплекс тока
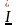 ,
сопряжённый с комплексным током
,
т. е. на
,
сопряжённый с комплексным током
,
т. е. на
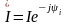 :
:
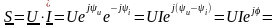
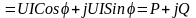 .
(3.142)
.
(3.142)
Таким
образом, вещественная
часть комплексной мощности
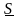 равна активной мощности Р, а мнимая
реактивной Q;
при
этом
положительный знак
сохраняется для индуктивной
мощности
и изменяется на отрицательный
знак для ёмкостной.
Полная
мощность равна модулю комплексной
мощности
;
аргумент комплексной мощности равен
углу сдвига фаз .
равна активной мощности Р, а мнимая
реактивной Q;
при
этом
положительный знак
сохраняется для индуктивной
мощности
и изменяется на отрицательный
знак для ёмкостной.
Полная
мощность равна модулю комплексной
мощности
;
аргумент комплексной мощности равен
углу сдвига фаз .
3.18.7. Применение методов расчёта цепей постоянного тока к расчёту цепей синусоидального тока
Для анализа и расчёта электрических цепей постоянного тока разработан ряд методов и приёмов, облегчающих решение системы уравнений. К числу таких методов относятся: метод контурных токов, метод узловых потенциалов, метод активного двухполюсника, метод наложения, методы эквивалентных преобразований и др. Известно, что окончательные расчётные формулы этих методов получены в результате выводов, основанных на законах Кирхгофа.
Поскольку законы Кирхгофа справедливы и для цепей синусоидального тока, то все расчётные формулы, полученные для цепей постоянного тока, пригодны и к расчёту цепей синусоидального тока, если в этих формулах заменить постоянные величины комплексными величинами (см. таблицу):
В качестве примера запишем уравнения в комплексной форме для некоторых методов.
Уравнения контурных токов для электрической цепи с тремя независимыми контурами:
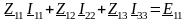 ,
,
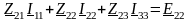 ,
,
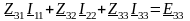 .
.
Таблица Уравнения узловых потен-
ц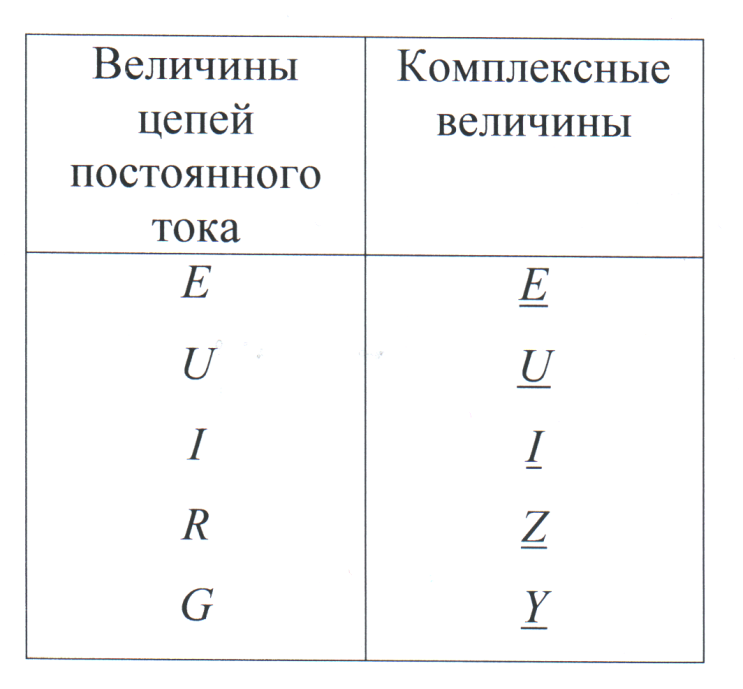 иалов
для электрической цепи с тремя независимыми
узлами:
иалов
для электрической цепи с тремя независимыми
узлами:
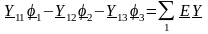 ,
,
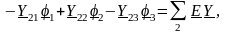
 По методу
активного двухпо-люсника
(эквивалентного гене-ратора) ток в
ветви аb:
По методу
активного двухпо-люсника
(эквивалентного гене-ратора) ток в
ветви аb:
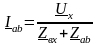 .
.
Э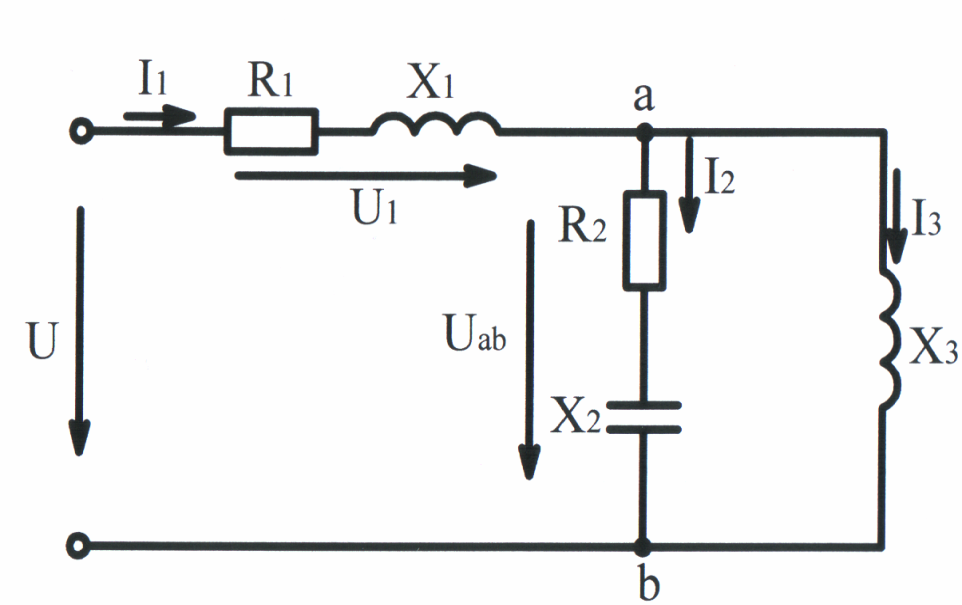 квивалентные
преобразования треугольника сопротивлений
квивалентные
преобразования треугольника сопротивлений
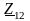 ,
,
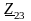 ,
,
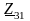 в трёхлучевую звезду
сопротивлений
в трёхлучевую звезду
сопротивлений
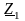 ,
,
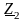 ,
,
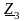 :
:
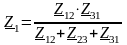 ;
;
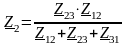 ;
;
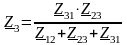 .
.
Рис. 3.60 Если же отдельные
ветви электрической
цепи синусоидального тока имеют магнитную связь (цепи с взаимоиндукцией), то расчёт таких цепей приобретает ряд особенностей, которые простой заменой величин постоянного тока комплексными величинами переменного тока не будут учтены. Методы расчёта электрических цепей синусоидального тока с взаимоиндукцией будут рассмотрены особо.
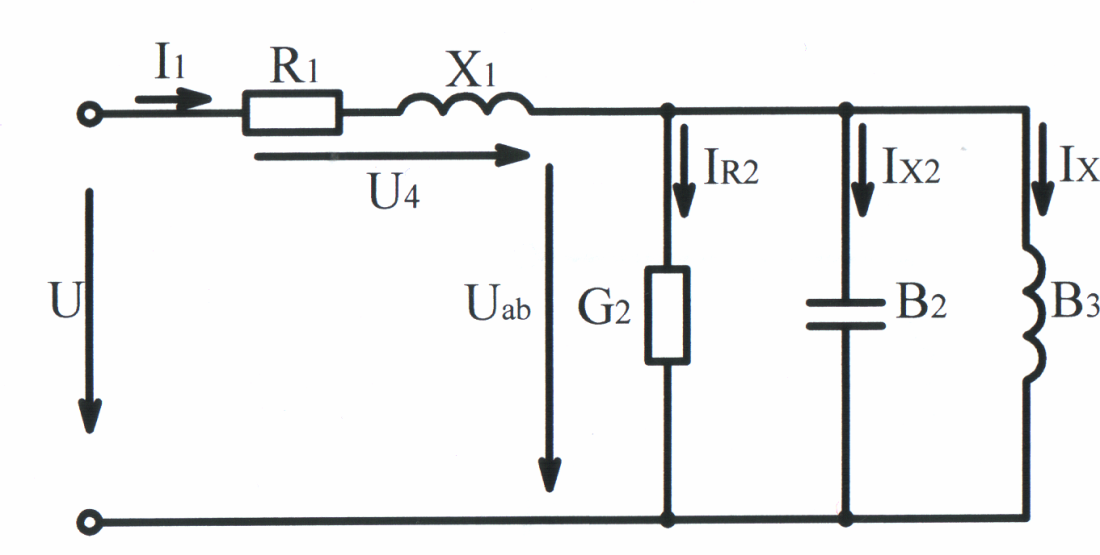
Рис. 3.61
Пример 3.7. Рассчитать электрическую цепь рис. 3.60
классическим и символическим методами, если заданы действующее значение синусоидального напряжения U = 120 B и сопротивление цепи: R1 = 4 Ом, X1 =10 Ом, R2 = 8 Ом, Х2 = 6 Ом, Х3 = 8,33 Ом.
Р е ш е н и е :
