
- •Глава 3. Однофазные электрические цепи синусоидального тока
- •Периодические переменные эдс, напряжения и токи
- •3.2. Явление электромагнитной индукции
- •3.3. Явление самоиндукции и эдс самоиндукции. Индуктивность
- •3.4. Источник синусоидальной эдс
- •3.5. Волновые диаграммы токов и напряжений
- •3.6. Действующее и среднее значения синусоидального тока
- •3.7. Изображение синусоидальных эдс, напряжений и токов вращающимися векторами
- •3.8. Законы Кирхгофа для электрической цепи синусоидального тока
- •3.9. Особенности электрических цепей переменного тока
- •3.10. Электрическая цепь с активным сопротивлением
- •3.11. Электрическая цепь с индуктивностью
- •Электрическая цепь с ёмкостью
- •3.13. Электрическая цепь с последовательным соединением сопротивления, индуктивности и ёмкости
- •3.14. Резонанс напряжений
- •2. Расчёт цепи при резонансе напряжений.
- •3.15. Эквивалентные схемы пассивных двухполюсников переменного тока
- •3.16. Электрическая цепь с параллельным соединением приёмников
- •3.17. Резонанс токов
- •3.18. Компенсация сдвига фаз
- •3.18. Комплексный метод расчёта цепей синусоидального тока
- •3.18.1. Общие сведения о комплексных числах
- •3.18.2. Изображение синусоидальных напряжений и токов комплексными числами
- •3.18.3. Закон Ома в комплексной форме
- •3.18.4. Комплексное сопротивление и комплексная проводимость
- •3.18.5. Законы Кирхгофа в комплексной форме
- •3.18.6. Определение мощности по комплексным напряжению и току
- •3.18.7. Применение методов расчёта цепей постоянного тока к расчёту цепей синусоидального тока
- •1. Классический метод.
- •2. Символический (комплексный) метод.
- •Важнейших открытий XIX века, заложивших фундамент «Теоретических основ электротехники»
- •Важнейших изобретений XIX, начала XX века в области электротехники
- •3.2. Явление электромагнитной индукции __________________________ 75
- •Часть 1. Линейные и нелинейные электрические цепи постоянного тока. Однофазные цепи синусоидального тока.
3.17. Резонанс токов
В электрической цепи с параллельным соединением катушки индуктивности и конденсатора (рис. 3.35) возникает резонанс токов, если частота собственных колебаний контура 0 совпадает с частотой вынужденных колебаний источника питания.
Через параметры цепи условие резонанса токов выражается равенством реактивных проводимостей параллельных ветвей (рис. 3.36):
BL
= BC
или
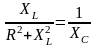 ;
(3.122)
;
(3.122)
следовательно, при резонансе токов реактивная проводимость цепи В = BL BC = 0.
Полная проводимость цепи
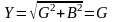 ,
,
т. е. имеет наименьшее значение, а полное сопротивление Z – наибольшее значение.
Токи в ветвях и неразветвлённой части цепи (рис. 3.36):
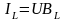 ;
;
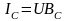 ;
;
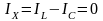 ;
;
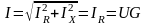 .
.
Если BL = BC G, то IL = IC I, т. е. ток всей цепи меньше токов параллельных ветвей, так как индуктивный и ёмкостный токи компенсируют друг друга.
При резонансе токов
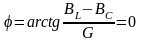 ,
,
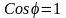 ,
,
т. е. цепь со стороны источника питания имеет активный характер (ток I и напряжение U совпадают по фазе).
Векторная диаграмма напряжения и токов при резонансе токов представлена на рис. 3.40. Как видно из векторной диаграммы, в режиме резонанса токов рассматриваемая цепь (рис. 3.35) ведёт себя по отношению к источнику питания так, как будто она состоит только из элементов с активной проводимостью. В действительности же в параллельных ветвях с L и C протекают
т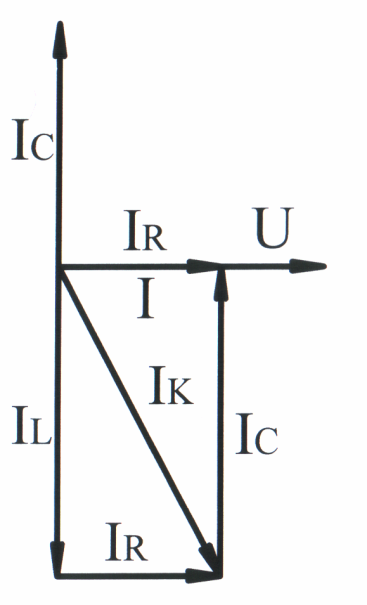 оки,
которые могут даже превышать полный
ток, протекающий в источнике питания.
Но эти токи всегда противоположны по
фазе друг другу. Это означает, что
через каждые четверть периода
происходит обмен энергиями между
магнит-ным полем индуктивной
катушки и электрическим
оки,
которые могут даже превышать полный
ток, протекающий в источнике питания.
Но эти токи всегда противоположны по
фазе друг другу. Это означает, что
через каждые четверть периода
происходит обмен энергиями между
магнит-ным полем индуктивной
катушки и электрическим
полем конденсатора,
Рис. 3.40 который поддерживается
напряжением U источника
питания.
Индуктивная QL и ёмкостная QС мощности при резонансе одинаковы
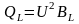 ,
,
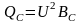 ,
,
поэтому реактивная мощность цепи
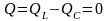 ,
,
а полная мощность цепи S равна активной мощности Р:
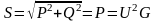 .
.
В
частном случае, когда активная проводимость
цепи G
=
0, полный ток
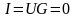 (входное сопротивление цепи Z
=
).
В замкнутом LC-контуре
протекает ток IL
= IC
(имеют
место незатухающие синусоидальные
колебания с частотой 0).
(входное сопротивление цепи Z
=
).
В замкнутом LC-контуре
протекает ток IL
= IC
(имеют
место незатухающие синусоидальные
колебания с частотой 0).
3.18. Компенсация сдвига фаз
На практике широкое применение имеют электроприёмники, содержащие индуктивности, например, электродвигатели переменного тока. Ток таких приёмников содержит активную и реактивную составляющие. Только активная составляющая тока IR определяет преобразование электроэнергии в другие виды энергии (например, механическую в электродвигателях). Реактивная же составляющая тока IL, необходимая для создания магнитного поля, никакой работы не производит. Однако при её наличии увеличивается полный ток приёмника
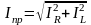 .
.
Представим электроприёмник, имеющий активную и индуктивную составляющие тока, схемой последовательного соединения элементов Rпр и XLпр (рис. 3.41). Параллельно этому приёмнику включим конденсатор с регулируемой ёмкостью С.
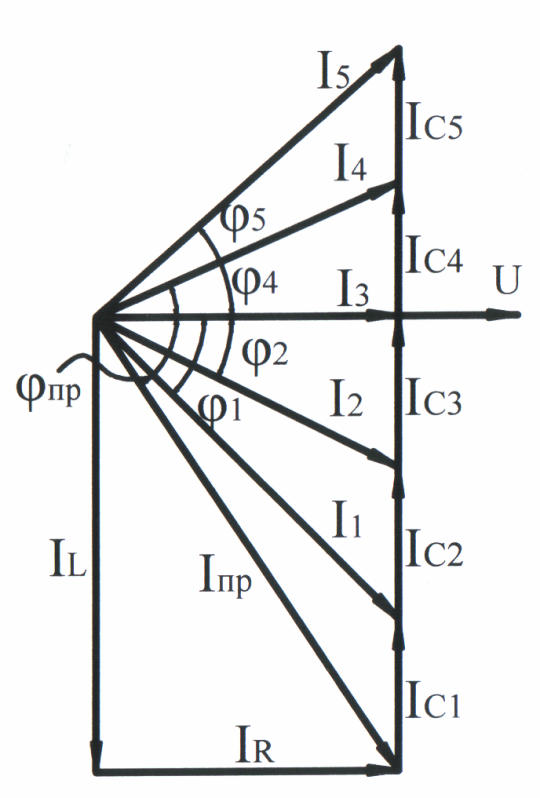
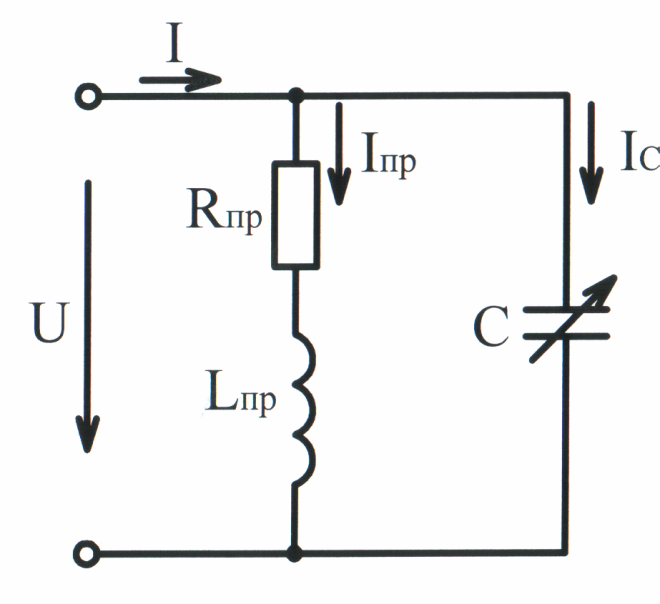
Рис. 3.41 Рис. 3.42
На
векторной диаграмме (рис. 3.42) ток приёмника
Iпр
отстаёт от напряжения U
на угол
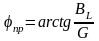 .
.
При отсутствии ёмкости ток в линии передачи I с сопротивлением Rл равен току приемника Iпр. Потери мощности в линии
. (3.123)
Для
уменьшения потерь мощности в линии надо
при неизменном токе Iпр
уменьшать ток в линии
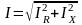 путём уменьшения реактивного тока цепи
путём уменьшения реактивного тока цепи
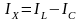 .
Это достигается включением конденсатора
ёмкостью С
параллельно приёмнику. С увеличением
ёмкости С
увеличивается ток IС,
а реактивный ток IX
уменьшается,
поэтому уменьшается общий ток I.
Угол сдвига фаз
(между напряжением U
и током I)
.
Это достигается включением конденсатора
ёмкостью С
параллельно приёмнику. С увеличением
ёмкости С
увеличивается ток IС,
а реактивный ток IX
уменьшается,
поэтому уменьшается общий ток I.
Угол сдвига фаз
(между напряжением U
и током I)
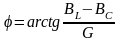 ,
,
при
этом будет уменьшаться (BL
= const,
G
= const,
BС
увеличивается), а Cos
увеличиваться. Из треугольника токов
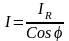 ;
следовательно, при IR
= const
с увеличением Cos
ток I
уменьшается, поэтому снижаются потери
мощности в линии (3.123).
;
следовательно, при IR
= const
с увеличением Cos
ток I
уменьшается, поэтому снижаются потери
мощности в линии (3.123).
Таким образом, для уменьшения потерь мощности в передающих устройствах необходимо увеличивать коэффициент мощности приёмников электроэнергии.
Из векторной диаграммы (рис. 3.42) видно, что с увеличением тока IС (IС1, IС2, IС3) ток I (I1, I2, I3) уменьшается. При IL = IC3 наступает резонанс токов, = 3 = 0; ток I = I3 в этом режиме минимальный.
Компенсация отстающей реактивной составляющей тока в электрических цепях с помощью параллельно включаемых к приёмникам конденсаторов, при которой повышается коэффициент мощности, называется компенсацией сдвига фаз.
Если ёмкостный ток в цепи превышает индуктивный ток (на векторной диаграмме IС = IC4, IC5), то наступает режим перекомпенсации; при этом Cos уменьшается, а ток I возрастает (цепь приобретает ёмкостный характер). Этот режим неблагоприятный для цепи, также как и режим недокомпенсации.
Пример
3.2.
Рассчитать электрическую цепь (рис.
3.43) с параллельным соединением катушки
индуктивности с сопротивлением R1
= 60
Ом и индуктивностью L
= 0,2
Гн и ветви, содержащей последовательно
соединённые резистор R2
= 30
Ом и конденсатор ёмкостью С
=
20 мкФ при синусоидальном входном
напряжении
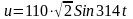 .
Определить ёмкость конденсатора, при
которой в цепи наступит резонанс токов,
если R2
= 0;
рассчитать цепь при резонансе.
.
Определить ёмкость конденсатора, при
которой в цепи наступит резонанс токов,
если R2
= 0;
рассчитать цепь при резонансе.
Р
 е ш е н и е.
1.
Расчёт цепи до резонанса.
е ш е н и е.
1.
Расчёт цепи до резонанса.
Рис. 3.43 Рис. 3.44
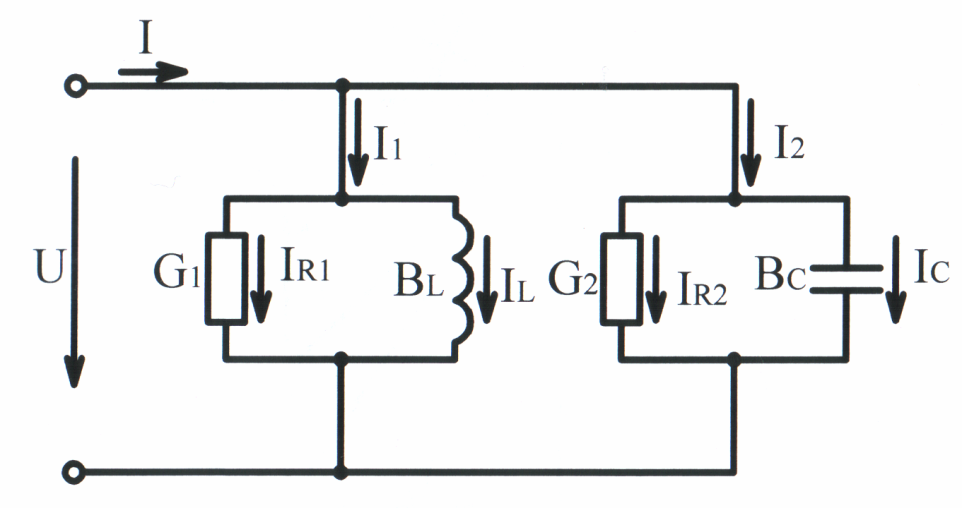
Заменяем ветви схемы рис. 3.43 с последовательным соединением параметров эквивалентной схемой рис. 3.44 с параллельным соединением параметров. С этой целью определяем проводимости ветвей, предварительно определив индуктивное XL = L = 314 0,2 = 62,8 Ом и ёмкостное сопротивление
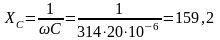 Ом.
Ом.
Активная проводимость первой ветви
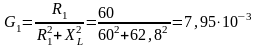 См.
См.
Индуктивная проводимость первой ветви
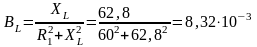 См.
См.
Активная проводимость второй ветви
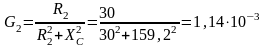 См.
См.
Ёмкостная проводимость второй ветви
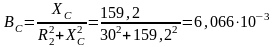 См.
См.
Активная проводимость всей цепи равна арифметической сумме активных проводимостей отдельных ветвей:
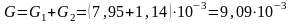 См.
См.
Реактивная проводимость всей цепи равна алгебраической сумме реактивных проводимостей отдельных ветвей (при этом индуктивные проводимости берутся со знаком «плюс», а ёмкостные – со знаком «минус»):
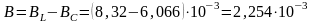
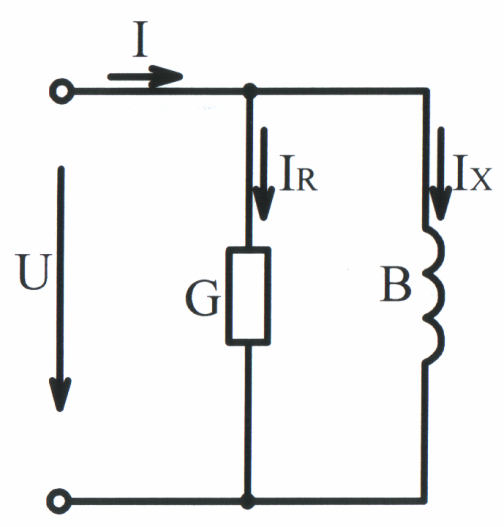 См.
См.
Так как реактивная проводимость цепи положи-тельна, то эквивалентная схема (рис. 3.45) имеет индуктивный характер.
Активный ток цепи
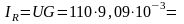
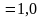 A.
A.
Реактивный ток цепи
Рис.
3.45
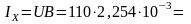
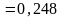 A.
A.
Полный ток цепи
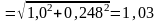 A.
A.
Активный IR1 и индуктивный IL токи первой ветви (рис. 3.44):
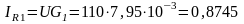 A;
A;
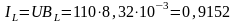 A.
A.
Полный ток первой ветви
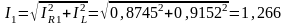 A.
A.
Активный IR2 и индуктивный IС токи второй ветви
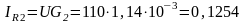 A;
A;
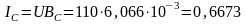 A.
A.
Полный ток второй ветви
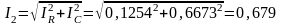 A.
A.
Для проверки правильности расчёта токов определим активный и реактивный токи для схемы (рис. 3.44) и сравним их с токами, рассчитанными для схемы (рис. 3.45).
Активный ток цепи равен арифметической сумме активных токов отдельных ветвей:
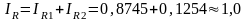 .
.
Реактивный ток цепи равен алгебраической сумме реактивных токов ветвей:
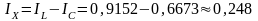 А.
А.
Углы сдвига фаз: для первой ветви
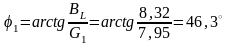 ;
;
для второй ветви (ёмкостная проводимость берётся со знаком «минус»)
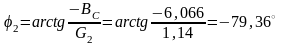 ;
;
для всей цепи
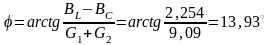 .
.
Активная и индуктивная мощности первой ветви:
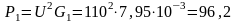 Вт;
Вт;
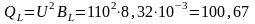 вар.
вар.
Активная и ёмкостная мощности второй ветви:
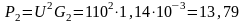 Вт;
Вт;
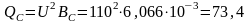 вар.
вар.
Активная, реактивная и полная мощности всей цепи:
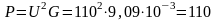 Вт;
Вт;
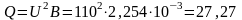 вар;
вар;
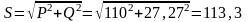 В
А.
В
А.
Проверка правильности расчёта цепи (рис. 3.43) по мощности.
Активная мощность цепи равна арифметической сумме активных мощностей отдельных ветвей:
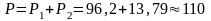 Вт.
Вт.
Реактивная мощность цепи равна алгебраической сумме реактивных мощностей отдельных ветвей:
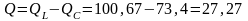 вар.
вар.
По результатам расчёта строим векторную диаграмму напряжений и токов (рис. 3.46). В качестве исходного вектора принимаем вектор напряжения U, так как напряжение на всех параллельных ветвях схемы (рис. 3.44) одинаковое. Активный ток первой ветви IR1 совпадает по фазе с напряжением, а индуктивный ток IL отстаёт от напряжения на угол 90. Геометрическая сумма
т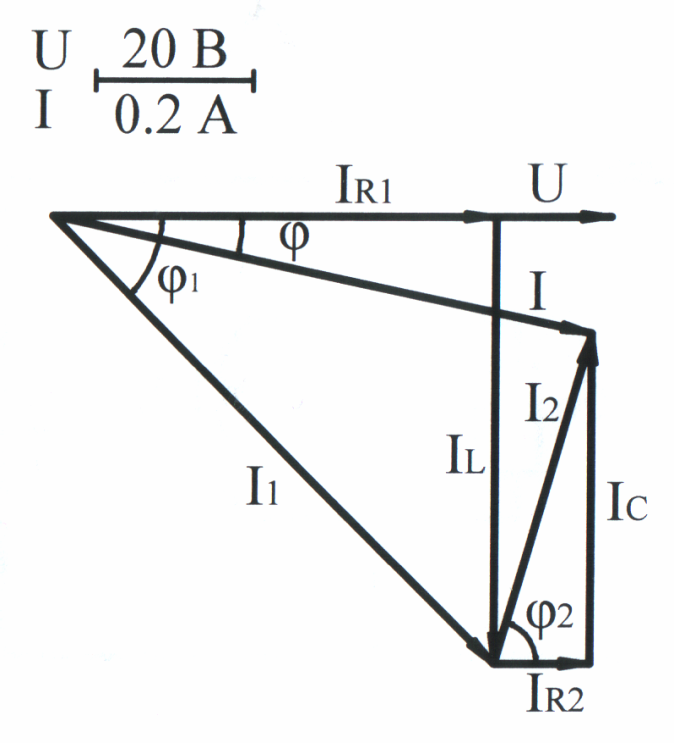 оков
IR1
и IL
равна полному току первой ветви I1,
отстающему от напряжения на угол 1
(на диаграмме образован прямоугольный
треугольник токов первой ветви). Из
конца вектора тока I1
проводим параллельно вектору U
вектор тока IR2,
из которого в сторону опережения U
на 90
проводим
оков
IR1
и IL
равна полному току первой ветви I1,
отстающему от напряжения на угол 1
(на диаграмме образован прямоугольный
треугольник токов первой ветви). Из
конца вектора тока I1
проводим параллельно вектору U
вектор тока IR2,
из которого в сторону опережения U
на 90
проводим
вектор IС. Соединяя начало вектора тока IR2 с концом
Рис. 3.46 вектора IС, получаем вектор
тока второй ветви I2, который
опережает напряжение на угол 2 (прямоугольный треугольник токов второй ветви).
Соединив начало вектора тока I1 с концом вектора тока I2, получаем вектор тока в неразветвлённой части цепи I, который отстаёт от напряжения на угол (цепь имеет индуктивный характер), т. е. полный ток I равен геометрической сумме токов I1 и I2.
Расчёт цепи при резонансе токов, если R2 = 0
В этом случае активная проводимость второй ветви G2 = 0; эквивалентная схема изображена на рис. 3.47.
Условием резонанса токов является равенство индуктивной и ёмкостной проводимостей:
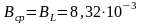
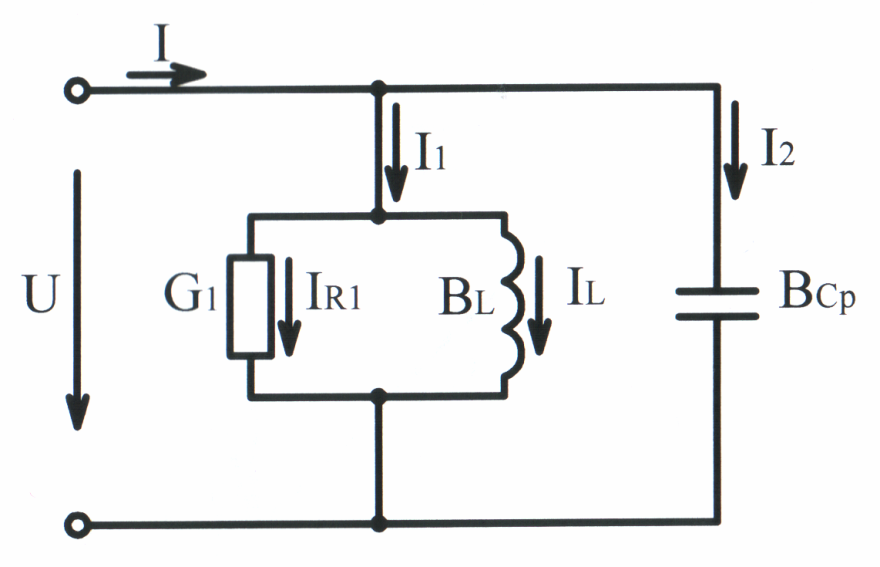 См.
См.
При R2 = 0
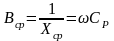 ,
откуда
,
откуда
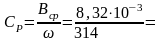
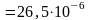 Ф = 26,5 мкФ.
Ф = 26,5 мкФ.
Токи в ветвях и неразветвлённой части цепи. Токи в первой ветви
Рис. 3.47 останутся такими же, как и
до резонанса, а именно:
IR1 = 0,8745 А, IL = 0,9152 А, I1 =1,266 А.
Ток
второй ветви
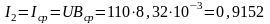 А, т. е. Iср
=
IL,
а IR2
=
0, так как G2
=
0.
А, т. е. Iср
=
IL,
а IR2
=
0, так как G2
=
0.
Реактивная проводимость цепи
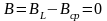 ,
,
реактивный ток цепи
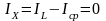 ,
,
полный ток цепи равен активному току первой ветви
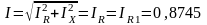 А.
А.
Мощности первой ветви останутся без изменения:
P1 = 96,2 Вт, QL = 100,67 вар.
Мощности второй ветви:
P2
=
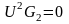 ,
QС
=
,
QС
=
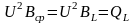 =
100,67 вар.
=
100,67 вар.
Мощности всей цепи:
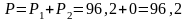 Вт,
Вт,
,
так как
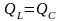 ;
;
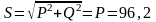 ВА.
ВА.
В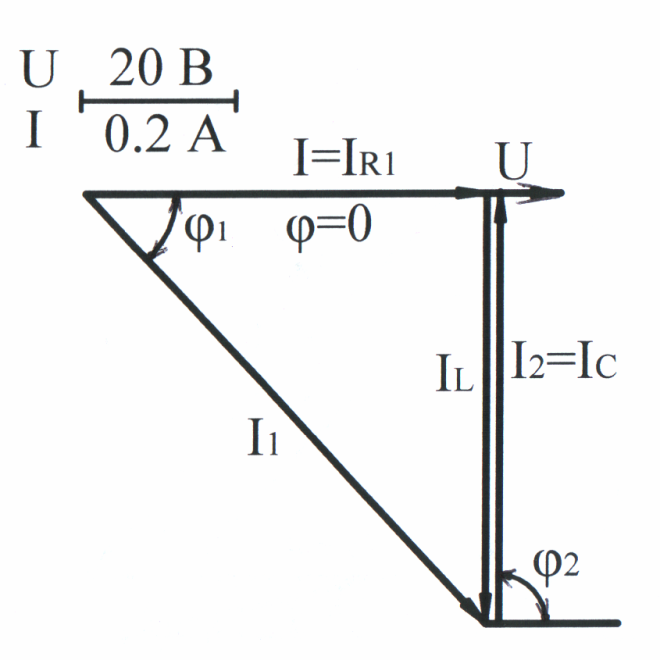 екторная
диаграмма напряжения и токов изображена
на рис. 3.48.
екторная
диаграмма напряжения и токов изображена
на рис. 3.48.
Рис. 3.48
