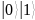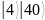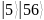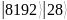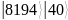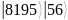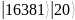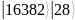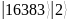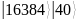5

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №5

Изучение квантового алгоритма Шора факторизации модуля криптосистемы

РША

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Студент:

(Ф.И.О., № группы) (подпись)

Преподаватель:

Яковлев В.А

(Ф.И.О) (подпись)

Цель лабораторной работы

Ознакомление с квантовым алгоритмом факторизации Шора и основами квантовых вычислений, наблюдение принципа работы квантового алгоритма в симуляции. Изучение способа факторизации модуля методом поиска периода для взлома криптосистем РША.

Выполнение лабораторной работы

Вариант 28:

№
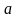
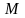
28	20	93

Проверка: НОД(93,20) = 1.

93 = 20*4 + 13

20 = 13*1 + 7

13 = 7*1 + 6

7 = 6*1 + 1

1. Проведем факторизацию числа M путем вычисления периода функции a^x mod M вручную.

x	20x	20x mod 93
0	1	1
1	20	20
2	400	28
3	8000	2
4	160000	40
5	3200000	56
6	64000000	4
7	1280000000	80
8	25600000000	19
9	512000000000	8
10	10240000000000	67
11	204800000000000	38
12	4096000000000000	16
13	81920000000000000	41
14	1638400000000000000	76
15	32768000000000000000	32
16	655360000000000000000	82
17	13107200000000000000000	59
18	262144000000000000000000	64
19	5242880000000000000000000	71
20	104857600000000000000000000	25
21	2097152000000000000000000000	35
22	41943040000000000000000000000	49
23	838860800000000000000000000000	50
24	16777216000000000000000000000000	70
25	335544320000000000000000000000000	5
26	6710886400000000000000000000000000	7
27	134217728000000000000000000000000000	47
28	2684354560000000000000000000000000000	10
29	53687091200000000000000000000000000000	14
30	1073741824000000000000000000000000000000	1
31	21474836480000000000000000000000000000000	20

Период повторения функции r = 30.

Поскольку r – четное, то можем представить его в виде r = 2k, k = 15.

Тогда, получаем a^r = a^2k = 1 mod M или a^2k – 1 = 0 mod M

Перепишем в виде (a^k)² – 1² = 0 mod M, применим формулу разности квадратов:

(a^k – 1)(a^k + 1) = 0 mod M. Выражение означает, что имеется общий сомножитель.

C помощью алгоритма Евклида, можем найти числа p и q:

p=НОД(a^k + 1, M)=НОД(20¹⁵ + 1, 93)=НОД(32768000000000000001, 93):

32768000000000000001 = 93*352344086021505376 + 33

93 = 33*2 + 27

33 = 27*1 + 6

27 = 6*4 + 3

6 = 3*2 + 0

Получили p = НОД(a^k + 1, M) = 3

q=НОД(a^k – 1, M)=НОД(20¹⁵ – 1, 93)=НОД(32767999999999999999‬, 93):

32767999999999999999 = 93*352344086021505376 + 31

93 = 31*3 + 0

Получили q = НОД(a^k – 1, M) = 31

Проверка: p * q = 3 * 31 = 93 = M. Факторизация модуля M = 93 выполнена успешна.

2. Выполним вручную процесс квантового возведения в степень в виде записи состояния регистров для двух периодов.

M = 93, M² = 8649 8192 < 8649 < 16384

Тогда N = 2ⁿ ≥ M², N = 16384 = 2¹⁴, n = 14

Сначала квантовые регистры инициализируются – устанавливаются в нулевое состояние:

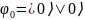
Далее, выполняется установка регистра 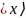в равновесное состояние. Достигается это путем применения к каждому кубиту первого регистра преобразовния Адамара. В результате регистр переводится к равновероятной суперпозиции всех возможных состояний. Состояние регистров можно описать так:

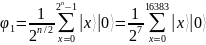
На следующем этапе вычисляются значения функции a^x mod M для всех аргументов x первого регистра. Результаты записываются во второй регистр. Каждому фиксированному состоянию регистра 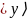соответствует последовательность значений регистра . Состояние можно записать следующим образом:

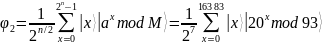
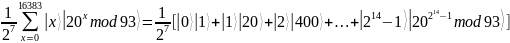
А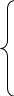

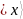
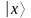
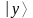
Таблица состояния регистров

…	…	…	…
…	…	…	…

После измерения состояния регистра 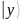, получаем фиксированное состояние, 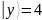, которому соответствует последовательность значений x вида:

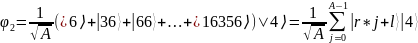
Где A ≈ N/r,

N – r ≤ Ar ≤ N + r, l = 6, l – сдвиг относительно начала координат (нулевого состояния регистра , ).

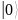Таким образом, были рассмотрены состояния регистров на этапе построения квантового возведения в степень и получена суперпозиция состояний в регистре 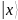, соответствующих фиксированному состоянию регистра .

3. Выполним факторизацию числа M на основе квантового алгоритма Шора с помощью программы-симулятора QuantumSimulator.exe.

Введем в программу модуль M = 93 и факторизуем:

Рассмотрим процесс симуляции выполнения алгоритма Шора. Программой было выбрано целое число a = 20, количество кубитов, необходимое для задания размера квантовых регистров n = 14, и, в этом случае, количество состояний каждого регистра N = 16384

Проверка:

M = 93, M² = 8649 8192 < 8649 < 16384

Тогда N = 2ⁿ ≥ M², N = 16384 = 2¹⁴, n = 14

НОД(93,20) = 1.

93 = 20*4 + 13

20 = 13*1 + 7

13 = 7*1 + 6

7 = 6*1 + 1

Далее в программе следует процесс инициализации – все кубиты квантовых регистров устанавливаются в нулевое состояние.

Затем выполняется преобразование Адамара к каждому кубиту первого регистра. В результате регистр переводится к равновероятностной суперпозиции всех возможных состояний.

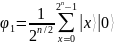
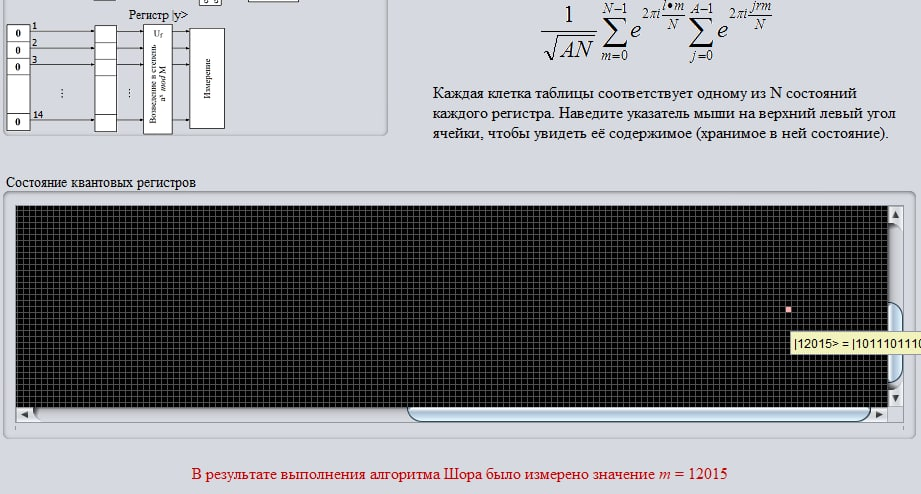
В результате выполнения квантового возведения в степень на следующем этапе для функции a^x mod M для всех состояний регистра , в регистре были получены следующие значения {1, 2, 4, 5, 7, 8, 10, 14, 16, 19, 20, 25, 28, 32, 35, 38, 40, 41, 47, 49, 50, 56, 59, 64, 67, 70, 71, 76, 80, 82}:

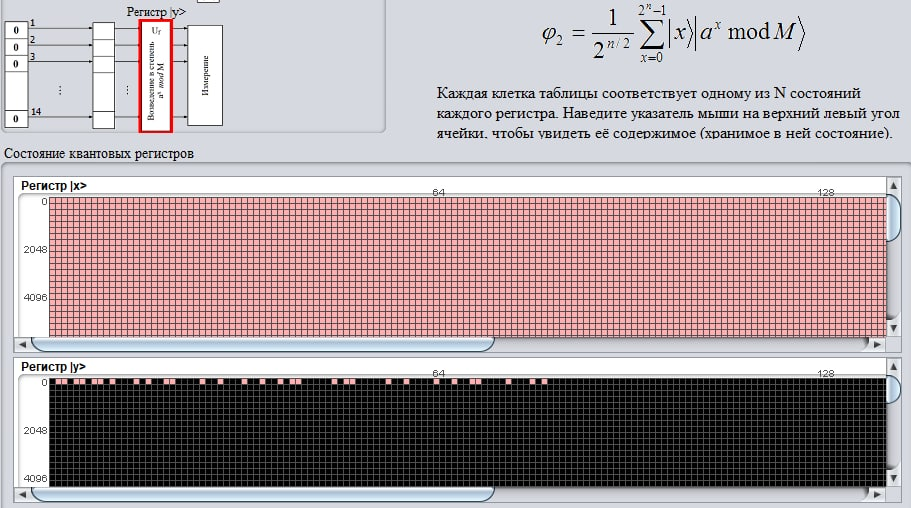
Далее было произведено измерение состояния регистра , было получено фиксированное значение y = 4, которому соответствует суперпозиция периодических последовательностей состояний в регистре :

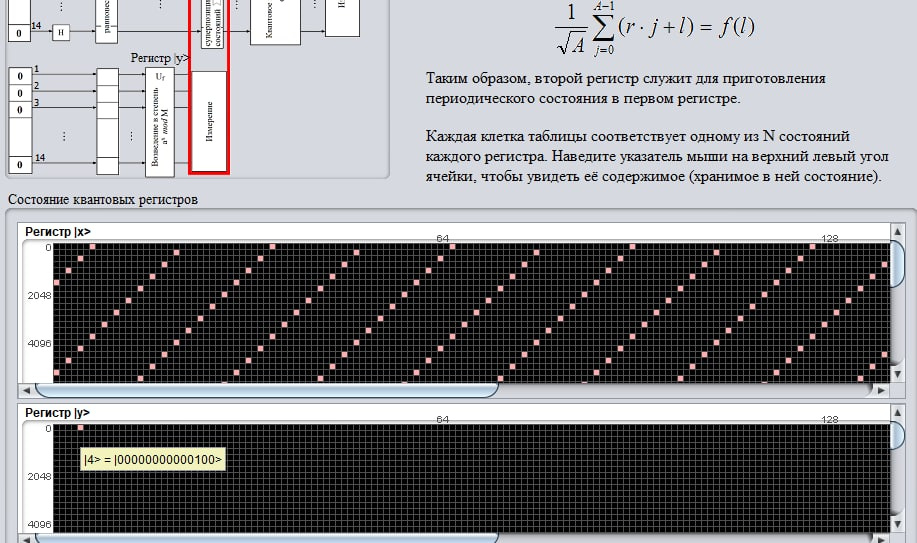
Суперпозиция описывается следующим образом:

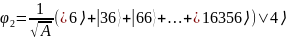
В результате применения для суперпозиции, содержащейся в регистре , квантового преобразования Фурье, были получено множество диапазонов значений:

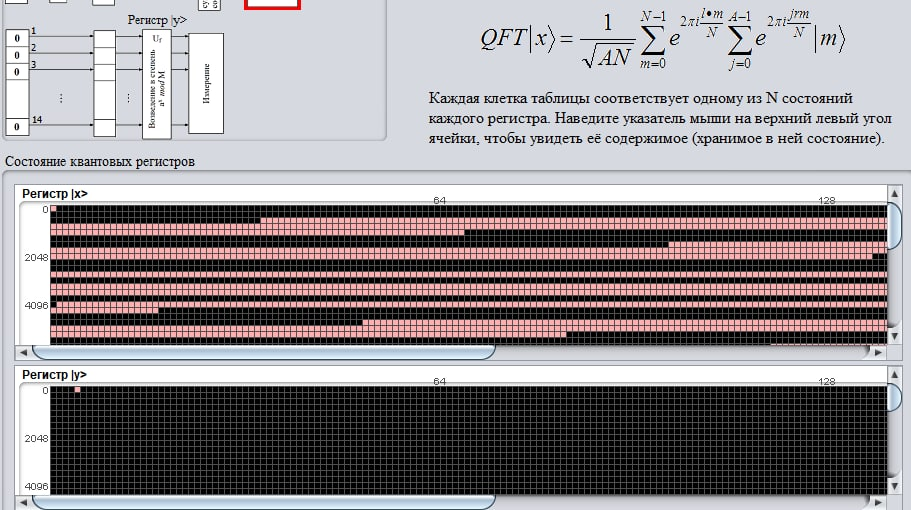
В результате измерения состояния регистра из упомянутого множества значений, было выбрано фиксированное значение m = 12015:

Дробь вида 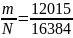передается на постобработку:

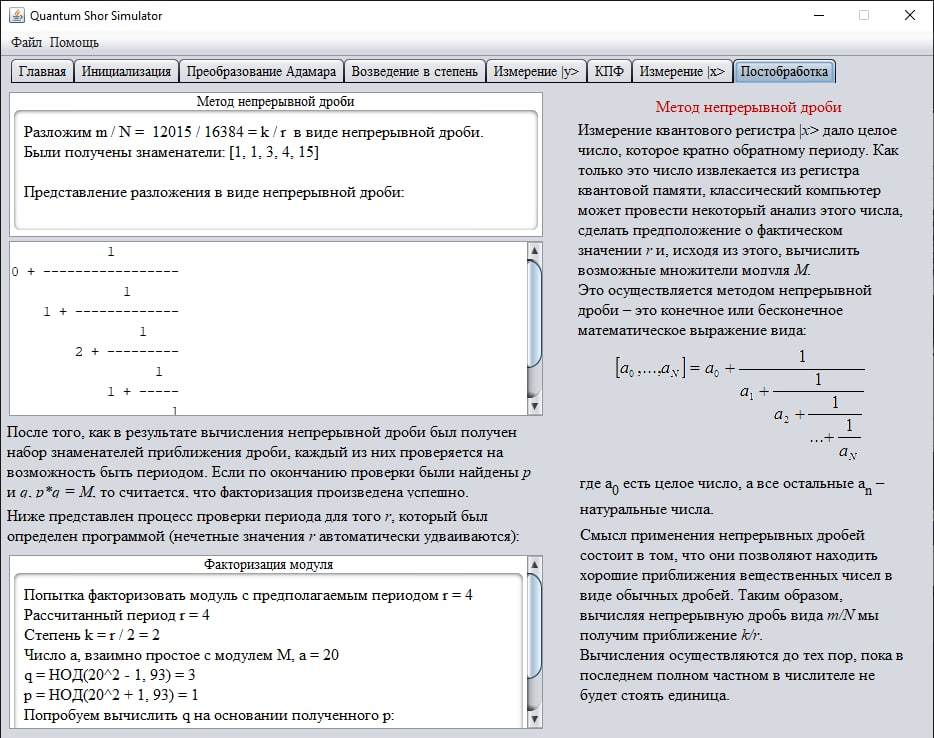
Разложим эту дробь:

12015 = 16384*0 + 12015

16384 = 12015*1 + 4369

12015 = 4369*2 + 3277

4369 = 3277*1 + 1092

3277 = 1092*3 + 1

1092 = 1*1092 + 0

Получили дробь [0, 1, 2, 1, 3, 1092]

Найдем подходящие дроби:

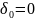
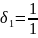
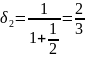
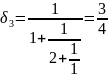
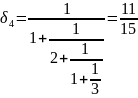
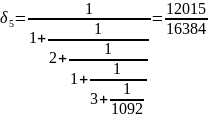
Получили следующие знаменатели подходящих дробей {1, 3, 4, 15, 16384}.

Период r = 4 < M – 1 = 16383 и r – четное число.

На основании полученного значения r = 4, рассчитываем коэффициенты разложения M = 93:

p = НОД(a^r/2 – 1, M) = НОД(20² – 1, 93) = НОД(399, 93):

399 = 93*4 + 27

93 = 27*3 + 12

27 = 12*2 + 3

12 = 3*4 + 0

Получили p = НОД(a^r/2 – 1, M) = 3

q = НОД(a^r/2 + 1, M) = НОД(20² + 1, 93) = НОД(401, 93):

401 = 93*4 + 29

93 = 29*3 + 6

29 = 6*4 + 5

6 = 5*1 + 1

Получили q = НОД(a^r/2 – 1, M) = 1

Попробуем найти q на основании вычисленного p:

q = M/p = 93/3 = 31

Проверка: p * q = 3 * 31 = 93 = M. Факторизация выполнена успешно.

Вывод

В ходе выполнения лабораторной работы было осуществлено ознакомление с квантовым алгоритмом факторизации Шора и основами квантовых вычислений. Произведено наблюдение принципа работы квантового алгоритма в симуляции, изучен способ факторизации модуля методом поиска периода для взлома криптосистем РША.

Санкт-Петербург

2022