7

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №7

Изучение системы шифрования Пэйе и ее гомоморфных свойств

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Студент:

(Ф.И.О., № группы) (подпись)

Преподаватель:

Яковлев В.А

(Ф.И.О) (подпись)

Цель лабораторной работы

Закрепление теоретических знаний, приобретение навыков шифрования и дешифрования информации с помощью КС Пэйе и изучение его гомоморфных свойств.

Вариант 28 mod 25 = 3

Выполнение лабораторной работы

Вариант	p	q	M
28(3)	13	17	13

Генерация ключей

Выбираем два простых числа p и q, такие, что НОД(pq, (p–1)(q–1)) = 1:

p = 13; q = 17

Проверка: НОД(13*7, (13-1)(17-1)) = НОД(221, 192) = 1

Вычисляем n = pq, λ = НОК(p–1, q–1)

n = 221

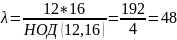
Выберем случайное число g такое, что

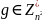
g = 3

Проверка: НОД(3, 221²) = НОД(3, 48841) = 1

Вычисляем

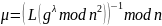
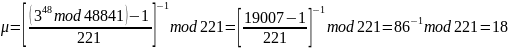
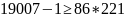
86^-1 mod 221 = 18

221 = 86*2 + 49 49 = 221 – 86*2

86 = 49*1 + 37 37 = 86 – (221 – 86*2) = 86*3 – 221

49 = 37*1 + 12 12 = (221 – 86*2) – (86*3 – 221) = 221*2 – 86*5

37 = 12*3 + 1 1 = (86*3–221)–(221*2–86*5)*3 = 86*18 – 221*7

Таким образом, открытый ключ {n, g} = {221, 3}

Закрытый ключ { λ, μ} = {48, 18}

Проверка в программе:

Шифрование

Необходимо зашифровать сообщение m = 13, для этого выберем случайное число k < 100 такое, что

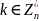
k = 8

Проверка: НОД(221, 8) = 1

Вычисляем криптограмму

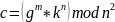
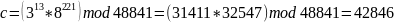
Получили шифротекст c = 42846

Проверка в программе:

Дешифрование

Вычислим исходное сообщение по полученной криптограмме c = 4952.

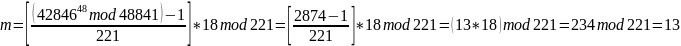
Таким образом, получили исходное сообщение m = 13

Проверка в программе:

Проверка гомоморфности криптосистемы Пэйе

Проверим первое свойство, заключающееся в том, что криптограмму можно возвести в некоторую степень r и дешифровать, что равносильно умножению сообщения на эту же константу

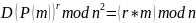
Будем использовать сообщение m = 5, r = 8.

Вычисляем криптограмму

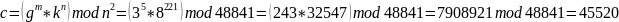
Проверка в программе:

Возведем криптограмму в степень r = 8:

45520¹ mod 48841 = 45520

45520² mod 48841 = 2072070400 mod 48841 = 39816

45520⁴ mod 48841 = 39816² mod 48841 = 1585313856 mod 48841 = 32678

45520⁸ mod 48841 = 32678² mod 48841 = 1067851684 mod 48841 = 40901

Дешифруем по схеме Пэйе:

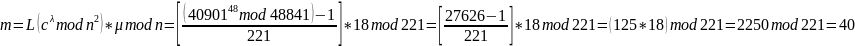
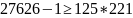
Получили сообщение m = 40, проверим в программе:

Первое свойство гомоморфности действительно выполняется:

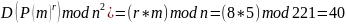
Проверка в программе:

Проверим второе свойство, заключающееся в том, что при дешифровании произведения двух криптограмм будет получена сумма соответствующих им открытых сообщений

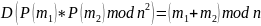
Будем использовать сообщения m₁ = 2, m₂ = 7

Вычисляем криптограммы

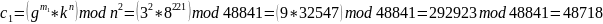
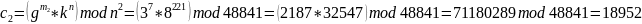
Проверка в программе:

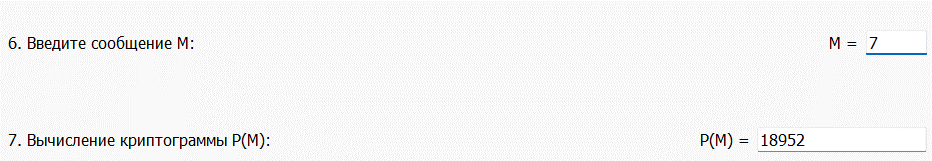
Перемножаем криптограммы:

И дешифруем криптограмму-произведение

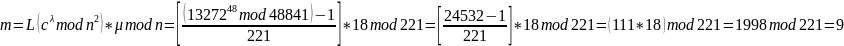
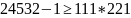
Получили сообщение m = 12, проверим в программе:

Второе свойство гомоморфности действительно выполняется

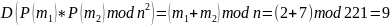
Проверка в программе:

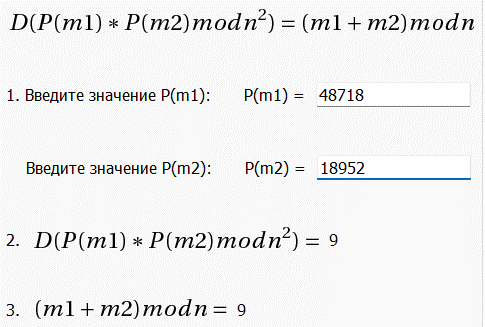
Вывод

В ходе выполнения лабораторной работы были закреплены теоретические знания, приобретены навыки шифрования и дешифрования информации с помощью криптосистемы Пэйе, а также изучены ее гомоморфные свойства.

Санкт-Петербург

2022