2

\МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2

Тестирование простых чисел и нахождение квадратичных вычетов

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Студент:

(Ф.И.О., № группы) (подпись)

Преподаватель:

Яковлев В.А

(Ф.И.О) (подпись)

Цель лабораторной работы

Закрепить знания, полученные на лекциях дисциплины «криптопротоколы» по разделам «Квадратичные вычеты» и «Генерирование и тестирование простых чисел».

Выполнение лабораторной работы

Задание 1

1. Рассчитаем вероятность попадания на простое число при случайном генерировании чисел разрядности l=100,300,500,1000 при помощи следующих команд:

l: …..;

lg(x) := log(x)/log(10);

EstimateProb:2*(9*l-10)/(9*l*(l-1)*lg(10));

2. Для проверки числа на простоту тестом Ферма сгенерируем необходимое количество случайных 3-х разрядных чисел при помощи команды:

U: 100+random(900);

и отберем среди них не менее 3 нечетных чисел m, среди которых должно быть одно простое число,

Сгенерируем не менее 5 случайных 2-х разрядных чисел a при помощи команды:

U:10+random(90);

U;

Произведем проверку чисел m на простоту, используя тест Ферма при помощи команды:

power_mod(a,m-1,m);

Для числа m1 = 967:

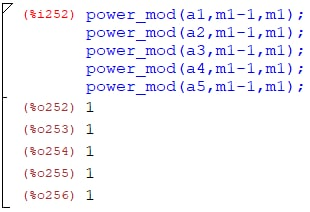
Результат проведенного теста Ферма: число 967 является вероятно простым с вероятностью

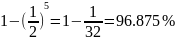
Вероятность ошибки:

Для числа m2 = 645:

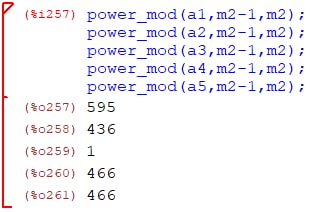
Результат проведенного теста Ферма: число 645 является составным.

Для числа m3 = 451:

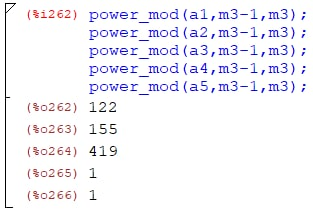
Результат проведенного теста Ферма: число 451 является составным.

3. Произведем тестирование числа Кармайкла m = 561 по методу Ферма. Для этого сгенерируем необходимое количество случайных 2-х разрядных чисел и выберем из них не менее 5 чисел a’ взаимно простых с 561, используя команду gcd(a’,561);

Далее, проведем тест Ферма:

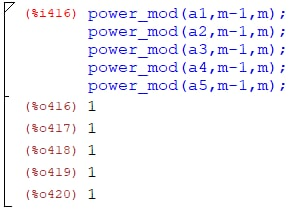
В ходе выполнения проверки числа Кармайкла m = 561 было ложно выявлено, что число является вероятно простым с вероятностью 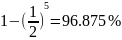. Для чисел Кармайкла тест Ферма использовать нецелесообразно, ведь для них результат теста является ложным для всех чисел a’, не являющихся делителем такого числа (Кармайкла).

4. Произведем тестирование на простоту одного из чисел m, сгенерированных в п.2 и число Кармайкла 561, по методу Миллера-Рабина при помощи набора команд:

m:561;

f:0;

a:m-1;

u:random(m-2);

x:0;

while mod(a,2)=0 do (

f:f+1,

a:a/2);

printf(false,”a:~d,”,a);

printf(false,”f:~d,”,f);

x:power_mod(u,a,m);

for i:0 step 1 thru f do (

printf(true,”i:~d, x:~d;”,I,x),

x:mod(x^2,m));

Для числа m =561:

Результат теста на простоту по методу Миллера-Рабина: число 561 – составное.

Для числа 451:

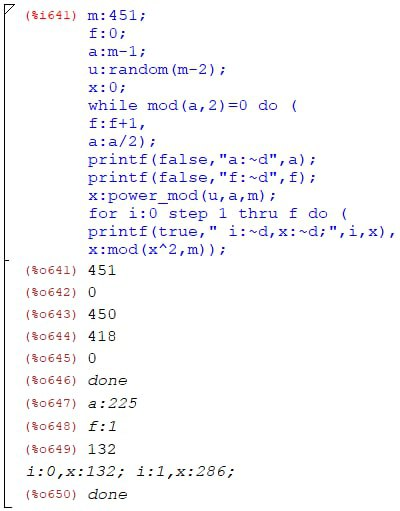
Результат теста на простоту по методу Миллера-Рабина: число 451 – составное.

Тест на простоту по методу Миллера-Рабина оказался эффективнее теста Ферма.

5. Найдем несколько квадратичных вычетов u<m по mod(m), где m одно из простых 3-х разрядных чисел, полученных в п.4, используя вычисление символа Якоби (который для простых m совпадает с символом Лежандра), при помощи следующей команды:

u: …..; m: …;

jacobi(u,m)

Нашли 3 квадратичных вычета по модулю 967 – это числа 25, 874, 353. И, для примера, квадратичный невычет – число 308.

Задание 2

1. Распределить числа в поле GF(p) на вычеты и невычеты. p=13.

Для p = 13, квадратичными вычетами являются классы вычетов: [0]₁₃, [1]₁₃, [3]₁₃, [4]₁₃, [9]₁₃, [10]₁₃, [12]₁₃

Квадратичными невычетами являются классы вычетов: [2]₁₃, [5]₁₃, [6]₁₃, [7]₁₃, [8]₁₃, [11]₁₃

Пример проверки для квадратичного вычета 9:

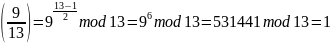
Пример проверки для квадратичного невычета 7:

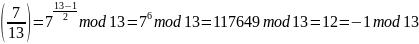
2. Проверить, является ли число a=(28+20)mod31=17 вычетом по модулю 17,19.

Число 17 принадлежит классу вычетов [0]₁₇ и [17]₁₉

По модулю 17 число a = 17 является вычетом:

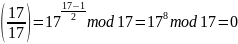
Проверим, является ли число 17 квадратичным вычетом по модулю 19:

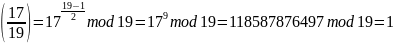
Число 17 является квадратичным вычетом по модулю 19.

3. Решить уравнение .

При p = 23, a = 51:

Проверим, что уравнение имеет решение:

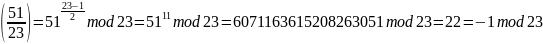
Уравнение не имеет корней.

При p = 29, a = 59:

Проверим, что уравнение имеет решение:

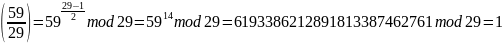
p = 29 = 4*7+1

т.к. вид p=4k+1, применим алгоритм Чиполлы.

Найдем случайное число b, такое, что b²-a – невычет.

b = 2

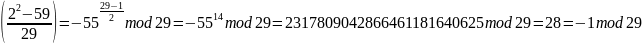
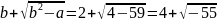АБОБА

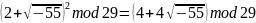
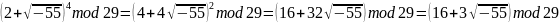
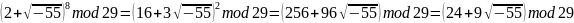
x = 1;-1

Проверка:

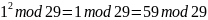
4. Найти все решения уравнения 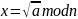, для n=7*5, a=324.

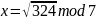
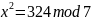
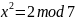
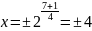
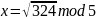
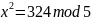
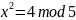
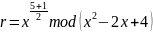
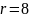
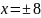
Составим 4 системы уравнений:

1. =>

2. =>

3. =>

4. =>

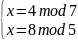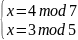
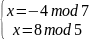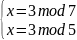
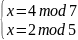
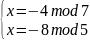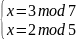
Решим последовательно четыре системы методом подстановки:

1. x = 7k+4

7k+4=3mod5

7k=4mod5

k=(4*7^-1)mod5; 1 = 5*3 + 7*(-2); 7^-1 = (5-2)mod5 = 3

k=(4*3)mod5=2; x = 7*2+4

x=18

2. x = 7k+3

7k+3=3mod5

7k=0mod5

k=0; x = 7*0+3

x=3

3. x = 7k+4

7k+4=2mod5

7k=3mod5

k=(3*7^-1)mod5

k=(3*3)mod5 = 4; x = 7*4+4

x=32

4. x = 7k+3

7k+3=2mod5

7k=4mod5

k=(4*7^-1)mod5

k=(4*3)mod5 = 2; x = 7*2+3

x=17

Найденные решения: x = 3, 17, 18, 32

Проверка:

x² = a mod n = 324 mod 35 = 9 mod 35

3² = 9 mod 35

17² = 289 mod 35 = 9 mod 35

18² = 324 mod 35 = 9 mod 35

32² = 1024 mod 35 = 9 mod 35

Вывод

В ходе выполнения лабораторной работы были закреплены знания по разделам «Квадратичные вычеты» и «Генерирование и тестирование простых чисел».

Санкт-Петербург

2022