
10
.docx
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,
СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
Факультет Инфокоммуникационных сетей и систем
Кафедра Защищенных систем связи
Дисциплина Криптографические протоколы
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №10
Система электронного голосования на основе гомоморфных свойств
криптосистемы Пэйе
(тема отчета)
Направление/специальность подготовки
10.03.01 Информационная безопасность
(код и наименование направления/специальности)
Студент:
(Ф.И.О., № группы) (подпись)
Преподаватель:
Яковлев В.А
(Ф.И.О) (подпись)
Цель лабораторной работы
Изучение принципов построения системы электронного голосования на основе криптосистемы Пэйе и анализ выполнения требований по обеспечению требований ее безопасности.
Выполнение лабораторной работы
Вариант №5
Избиратель |
B1 (100) |
B2 (101) |
B3 (102) |
B4 (103) |
B5 (104) |
Голос (m) |
A1 |
|
|
v |
|
|
m= 102 = 100 |
A2 |
v |
|
|
|
v |
m= 100+104 = 10001 |
A3 |
v |
|
|
|
|
m= 100 = 1 |
A4 |
|
v |
|
|
|
m= 101 = 10 |
A5 |
v |
|
|
v |
|
m= 100+103 = 1001 |
A6 |
|
|
v |
|
|
m= 102 = 100 |
A7 |
|
v |
|
|
|
m= 101 = 10 |
A8 |
v |
|
|
|
|
m= 100 = 1 |
A9 |
|
|
|
|
|
m= 0 |
Итог: |
4 |
2 |
2 |
1 |
1 |
mΣ = 11224 |
Избиратель |
Случайное число (ri) |
Голос (m) |
Зашифрованное значение голоса (ci) |
A1 |
19 |
100 |
11071485124 |
A2 |
21 |
10001 |
2590246437 |
A3 |
11 |
1 |
13018602364 |
A4 |
7 |
10 |
12352912484 |
A5 |
21 |
1001 |
3176882040 |
A6 |
8 |
100 |
5421848170 |
A7 |
7 |
10 |
12352912484 |
A8 |
11 |
1 |
13018602364 |
A9 |
9 |
0 |
3749536716 |
Подсчет: |
|
mΣ = 11224 |
T = 4333078237 |
Количество избирателей Nv = 9
Количество кандидатов Nc = 5
Основание системы счисления b = Nv + 1 = 10
Рассчитаем максимально возможное число mmax и максимально возможную сумму всех голосов в системе. Избиратели могут выбрать максимум 2 кандидатов одновременно.
Максимально возможное число mmax (При одновременном выборе кандидатов B4 и B5) = 103 + 104 = 11000
Следовательно, если все избиратели проголосуют с максимально возможным числом mmax, то максимально возможная сумма всех голосов в системе:
Tmax = Nv * mmax = 9 * 11000 = 99000
Генерация ключа (избирательная комиссия):
Выберем два простых числа p, q такие, что НОД(pq, (p-1)(q-1)) = 1
и n ≥ Tmax
Возьмем числа p = 331, q = 353:
n = pq = 331*353 = 116843 ≥ Tmax = 99000
НОД(331*353, 330*352) = НОД(116843, 116160) = 1
Числа p и q подходят.
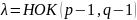

Выберем
случайное число
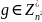 и
и
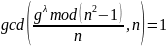
Выбираем g = 2:

Найдем
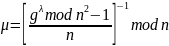
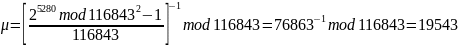
Таким образом,
Открытый ключ {n, g} = {116843, 2}
Закрытый
ключ
{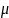 ,
,
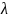 }
= {19543, 5280}
}
= {19543, 5280}
Шифрование бюллетеня:
Каждый избиратель шифрует свой голос:
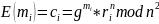
где
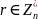
и отправляет криптограмму на сервер.

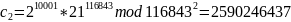
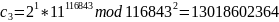
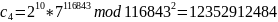
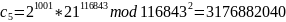

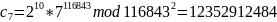
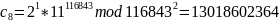
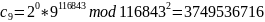
После чего сервер, получив криптограммы, производит вычисления над зашифрованными данными – перемножает их по модулю n2:
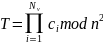
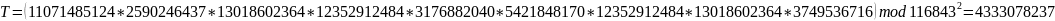
Дешифрование:
Дешифрование криптограммы произведения T осуществляется избирательной комиссией. Согласно гомоморфному свойству криптосистемы Пэйе:
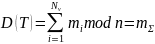
Расшифрование
выполняется по формуле
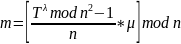
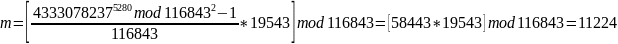
Проверка:
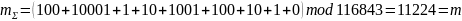
11224 = 1*104 + 1*103 + 2*102 + 2*101 + 4*100
В силу гомоморфности криптосистемы, индекс максимального элемента результирующего вектора и будет индексом победившего кандидата.
Таким образом, первое место занял кандидат B1, второе место разделяют кандидаты B2 и B3, а третье место разделяют кандидаты B4 и B5.
Вывод
В ходе выполнения лабораторной работы были изучены принципы построения системы электронного голосования на основе криптосистемы Пэйе, а также осуществлен анализ выполнения требований по обеспечению ее безопасности.
Санкт-Петербург
2022
