4

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №4

Исследование побочных атак на криптосистему РША

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Студент:

(Ф.И.О., № группы) (подпись)

Преподаватель:

Яковлев В.А

(Ф.И.О) (подпись)

Цель лабораторной работы

Изучить влияние параметров и способов проектирования криптосистемы РША на возможность ее криптоанализа, используя побочные атаки, а также закрепить знания, полученные на лекциях курса «Основы криптографии с открытым ключом», «Криптографические протоколы».

Выполнение лабораторной работы

1. Атака на малую шифрующую экспоненту

Параметры криптосистем:

Набор ключей	Модуль n	Экспонента e	Экспонента d	Простое p	Простое q
1	616747	3	410107	677	911
2	184861	3	122667	461	401
3	478	3	159	239	2

Шифруемое сообщение: 320

Криптограмма 1: 80409

Криптограмма 2: 47603

Криптограмма 3: 144

Общее решение системы сравнений: 32768000

Кубический корень из общего решения (методом Ньютона): 320

Атака успешна проведена – получили сходное сообщение 320.

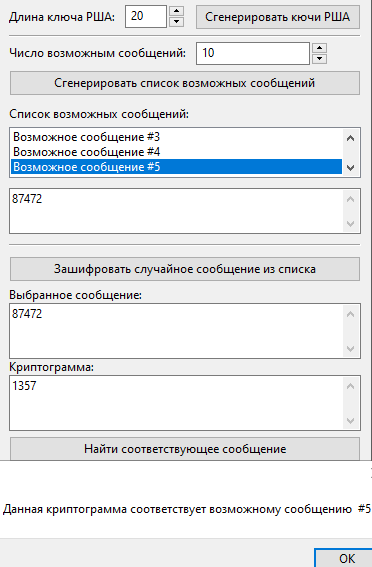
Перейдем к типу атаки «Малое количество возможных сообщений»:

Возможное сообщение 1: 89732

Возможное сообщение 2: 90387

Возможное сообщение 3: 7893

Возможное сообщение 4: 413

Возможное сообщение 5: 87472

Возможное сообщение 6: 52754

Возможное сообщение 7: 60468

Возможное сообщение 8: 68498

Возможное сообщение 9: 80766

Возможное сообщение 10: 29618

Зашифруем случайным образом одно из возможных сообщений:

Получили криптограмму: 1357

Будем последовательно шифровать возможные сообщения из списка, до тех пор, пока на выходе не получим начальную криптограмму 1357.

Сообщение 1 (89732) – криптограмма: 71036

Сообщение 2 (90387) – криптограмма: 41166

Сообщение 3 (7893) – криптограмма: 54526

Сообщение 4 (413) – криптограмма: 43691

Сообщение 5 (87472) – криптограмма: 1357

Шифруя сообщение 5-ое получили начальную криптограмму 1357. Таким образом, исходное сообщение: 87472.

2. Атака Винера

Длина модуля РША: 30

Длина секретной экспоненты: 8

Открытая экспонента e: 19247647

Модуль криптосистемы n: 268300423

Секретная экспонента d: 223

Простое число p: 10303

Простое число q: 26041

Выполним атаку Винера с помощью программы:

Подтвердим успешность выполнения атаки ручными расчетами:

Секретную экспоненту вычислим как знаменатель подходящей дроби в неравенстве

Используя алгоритм Евклида, найдем цепную дробь рационального числа

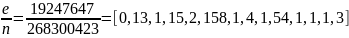
19247647 = 268300423*0 + 19247647

268300423 = 19247647*13 + 18081012

19247647 = 18081012*1 + 1166635

18081012 = 1166635*15 + 581487

1166635 = 581487*2 + 3661

581487 = 3661*158 + 3049

3661 = 3049*1 + 612

3049 = 612*4 + 601

612 = 601*1 + 11

601 = 11*54 + 7

11 = 7*1 + 4

7 = 4*1 + 3

4 = 3*1 + 1

3 = 1*3 + 0

Вычисляем подходящие дроби:

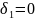
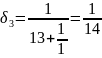
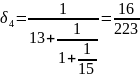
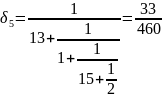
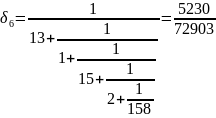
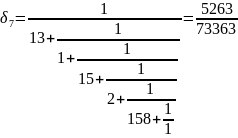
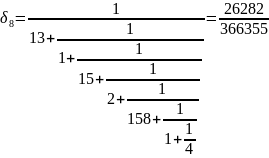
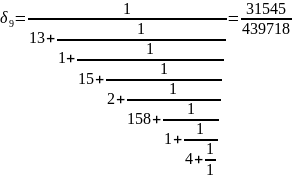
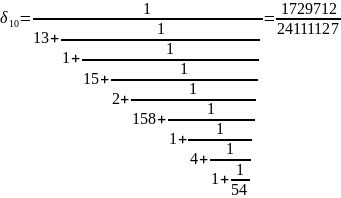
Теперь для каждой подходящей дроби будем находить функцию Эйлера согласно выражению 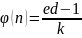, и решать квадратное уравнение .

Если корни уравнения p и q целочисленные, простые, и выполняется равенство 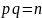, то секретная экспонента найдена правильно. В противном случае, проверяем следующую подходящую дробь.

Для :

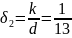Уравнение:

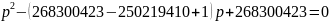
Корни уравнения не целочисленные, переходим к следующей подходящей дроби.

Для :

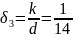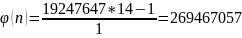
Уравнение:

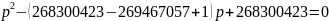
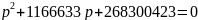
Корни уравнения не целочисленные, переходим к следующей подходящей дроби.

Для :

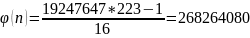
Уравнение:

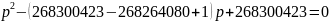
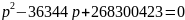
Корни уравнения целочисленные, простые, проверим выполнение равенства:

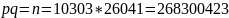
Равенство выполняется, следовательно, секретная экспонента d = 223 найдена правильно, делители модуля p = 10303, q = 26041 найдены верно.

Попробуем провести атаку Винера, используя битовую длину секретную экспоненты больше, чем четверть битовой длины модуля КС:

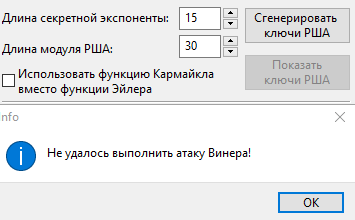
При битовой длине секретной экспоненты больше четверти битовой длины модуля КС атаку выполнить не удалось.

3. Атака с использованием мультипликативного свойства шифра РША

Параметры криптосистемы:

Открытая экспонента e: 157309

Секретная экспонента d: 144589

Модуль криптосистемы n: 171443

Выбранное сообщение M: 40025

Зашифрованное сообщение C: 40071

Случайное число x взаимно простое с модулем n: 8658

Комбинированная криптограмма C’ = C * x^e mod n = 26509

Расшифрованное M’: 50147

Исходное сообщение M = M’ * x^-1 mod n = 40025

Атака проведена успешно, получили исходное сообщение M = 40025:

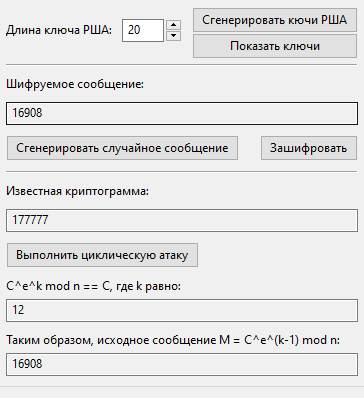
4. Циклическая атака

Открытая экспонента e: 159683

Модуль криптосистемы n: 186313

Шифруемое сообщение M: 16908

Криптограмма C: 177777

, где k = 12

Исходное сообщение

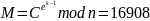
Атака проведена успешно, получили исходное сообщение M = 16908:

Увеличим длину модуля КС и проведем еще одну атаку:

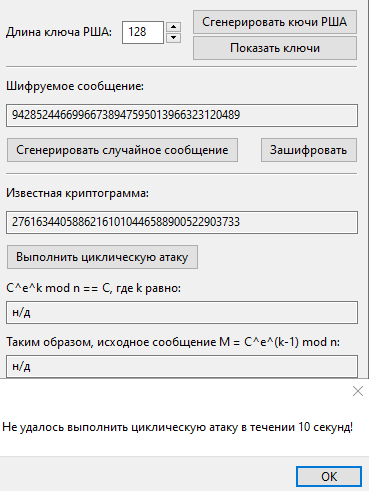
Таким образом, мы убедились, что алгоритм выполнения данной атаки обладает не полиноминальной сложностью.

5. Атака на общие модули

Открытая экспонента e₁: 19277

Открытая экспонента e₂: 12541

Секретная экспонента d₁: 23813

Общий модуль: 37403

Случайное число g, используемое для факторизации: 24708

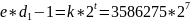
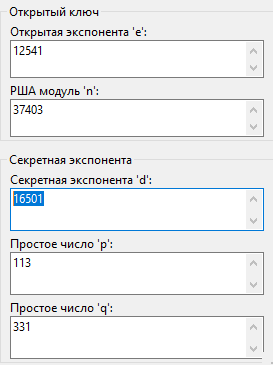
Делители модуля: 331 и 113

Секретная экспонента d₂: 16501

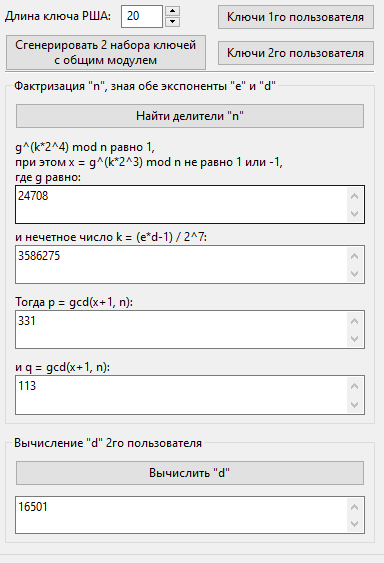
Атака проведена успешна, секретная экспонента второго пользователя d₂ действительна равняется 16501:

Вывод

В ходе выполнения лабораторной работы было изучено виляние параметров и способов проектирования КС РША на возможность ее криптоанализа, используя побочные атаки. Также, были закреплены знания по темам «Основы криптографии с открытым ключом», «Криптографические протоколы».

Санкт-Петербург

2022