6

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №6

Изучение криптосистемы Мак-Элис

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Студент:

(Ф.И.О., № группы) (подпись)

Преподаватель:

Яковлев В.А

(Ф.И.О) (подпись)

Цель лабораторной работы

Изучить преобразования, выполняемые при шифровании и дешифровании сообщений в криптосистеме Мак-Элис, а также простейшие попытки ее взлома.

Выполнение лабораторной работы

1. Параметры криптосистемы Мак-Элис:

Длина кодового слова n = 32 бита,

длина информационного сообщения k = 22 бита,

число искусственно вводимых ошибок t_A = 2.

Сгенерируем для выбранных параметров порождающую матрицу с применением кода Гоппы:

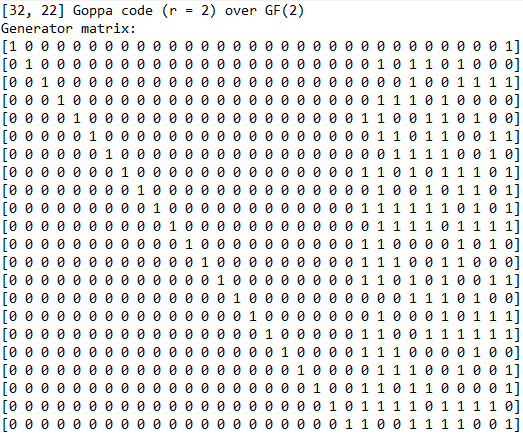
2. Параметры кода Гоппы:

Длина n = 2⁵ = 32 бита,

размерность k ≥ 2⁵–2∙5 = 22 бита,

минимальное расстояние d ≥ 2∙2+1 = 5.

3. Процесс генерации ключей и шифрования:

Загрузим в программу “McEliece” раннее сгенерированную порождающую матрицу G и убедимся в правильности параметров системы:

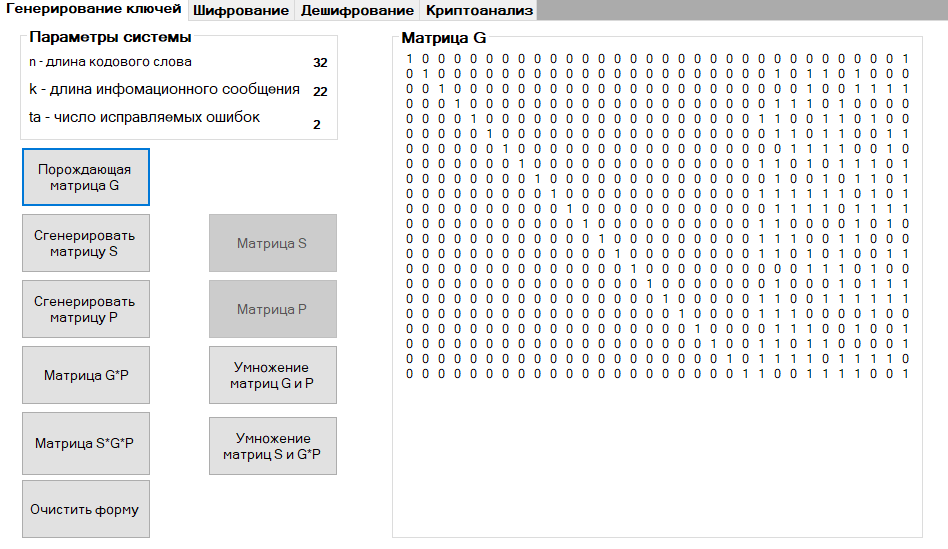
Сгенерируем несингулярную матрицу S:

Сгенерируем перестановочную матрицу P:

Рассчитаем произведение матриц G и P:

Получили матрицу G*P:

Рассчитаем произведение матриц S, G и P:

Получили матрицу S*G*P:

Таким образом, закрытым ключом является набор {несингулярная матрица S, порождающая матрица G, перестановочная матрица P}.

Открытым ключом является {Произведение матриц S*G*P, параметр t_A = 2}.

Зададим двоичное сообщение и сгенерируем случайный вектор ошибок Z, найдем криптограмму.

Сообщение m₁: 00101000000000000000000

Вектор Z₁: 00000001000000000000000000100000

Криптограмма c₁: 10100010101010100010111111111110

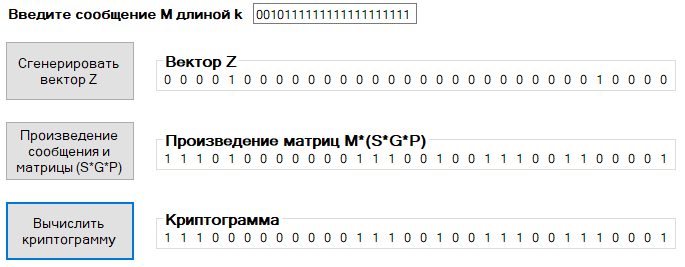
Сообщение m₂: 00101111111111111111111

Вектор Z₂: 00001000000000000000000000010000

Криптограмма c₂: 11100000000011100100111001110001

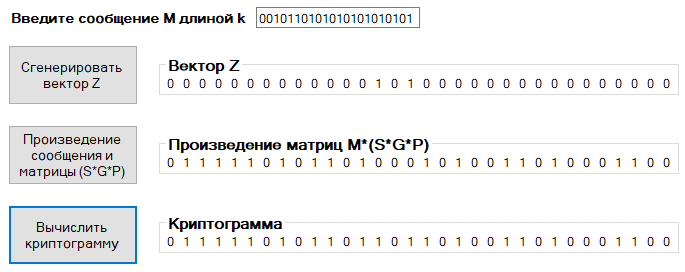
Сообщение m₃: 00101101010101010101010

Вектор Z₃: 00000000000001010000000000000000

Криптограмма c₃: 01111101011011011010011010001100

4. Процесс дешифрования:

Вычислим обратную P матрицу P^-1 и вектор c₁’=c₁*P^-1:

Используя алгоритм декодирования для кода Гоппы с порождающей матрицей G, исправим не более t_A = 2 ошибок в c’, в результате чего получим некоторый двоичной вектор m’ длины k. (В программе исправление ошибок реализовано за счет вычитания двоичного вектора ошибок Z):

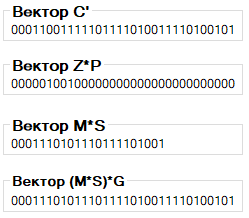
Далее, для восстановления сообщения найдем обратную S матрицу S^-1 и умножим двоичных вектор m’ на эту матрицу. m = m’*S^-1

Восстановленное сообщение m₁: 00101000000000000000000

Те же действия повторим для расшифрования сообщения m₂ и m₃:

Восстановленное сообщение m₂: 00101111111111111111111

Восстановленное сообщение m₃: 00101101010101010101010

5. Атака на криптосистему:

Номера столбцов:

28, 23, 10, 3, 18, 24, 15, 11, 2, 13, 7, 1, 5, 6, 32, 20, 21, 22, 16, 25, 12, 14

Нулевой вектор Z (ограниченный столбцами): 00000000000000000000000

Восстановленное сообщение m₁: 00101000000000000000000

Номера столбцов:

20, 30, 4, 7, 11, 2, 29, 26, 18, 8, 21, 22, 32, 13, 19, 9, 10, 3, 6, 31, 14, 23

Нулевой вектор Z (ограниченный столбцами): 00000000000000000000000

Восстановленное сообщение m₂: 00101111111111111111111

Номера столбцов:

3, 10, 6, 12, 19, 7, 5, 1, 17, 11, 27, 21, 31, 32, 24, 2, 8, 13, 15, 20, 23, 26

Нулевой вектор Z (ограниченный столбцами): 00000000000000000000000

Восстановленное сообщение m₃: 00101101010101010101010

Алгоритм атаки:

Система случайно выбирает k столбцов матрицы S*G*P (открытого ключа), проверяя при этом необходимые условия для взлома. Если матрица, составленная из выбранных k столбцов, окажется несингулярной и вектор Z, ограниченный этими столбцами, окажется нулевым, то сообщение будет восстановлено. Во всех трех случаях атака выполнилась успешно.

В программе для простоты полагается, что злоумышленнику известны биты, в которых появляется ошибка. В реальности же, взломщику не известен вектор ошибок Z, так как он абсолютно случайный, поэтому процесс подбора столбцов происходит до тех пор, пока не появится сообщение с известным характером избыточности.

6. Расчеты вероятности успеха атаки на КС Мак-Элис при выборе различных значений k и t.

Вероятность того, что вектор Z окажется нулевым равна:

Расчет при n = 32, k = 22, t = 2:

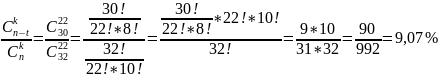
Расчет при n = 32, k = 17, t = 3:

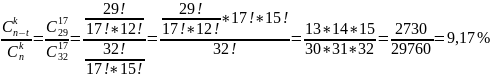
Расчет при n = 32, k = 12, t = 4:

При повышении величин параметров k (длина информационного сообщения) и t (количество искусственно вводимых ошибок) КС Мак-Элис, вероятность успеха атаки уменьшается.

Для обеспечения высокой стойкости КС Мак-Элис рекомендуются параметры n = 1024, t = 38, k > 644.

Вывод

В ходе выполнения лабораторной работы были изучены преобразования, выполняемые при шифровании и дешифровании сообщений в криптосистеме Мак-Элис, а также простейшие попытки ее взлома.

Санкт-Петербург

2022