9

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №9

Изучение криптопротокола с разделением секретных данных между

пользователями

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Студент:

(Ф.И.О., № группы) (подпись)

Преподаватель:

Яковлев В.А

(Ф.И.О) (подпись)

Цель лабораторной работы

Закрепить знания, полученные на лекциях дисциплине «Криптографические протоколы» по теме «протоколы разделения секрета».

Выполнение лабораторной работы

Вариант 28:

№ вар	Секрет k	a1	a2	p
28	1	13	6	17

Часть 1. Моделирование (n,m)-схемы разделения секретов

Схема разделения секрета на основе интерполяции полиномов над конечными полями (схема Шамира).

Число теней n = 5,

Порог восстановления m = 3,

Секрет k = 1,

Полином: 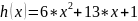, a₀ = k

Найдем тени k_i = h(x_i), где x_i = (1, 2, 3, 4, 5):

k₁ = h(x₁) = (6*1²+13*1+1) mod 17 = 3

k₂ = h(x₂) = (6*2²+13*2+1) mod 17 = 0

k₃ = h(x₃) = (6*3²+13*3+1) mod 17 = 9

k₄ = h(x₄) = (6*4²+13*4+1) mod 17 = 13

k₅ = h(x₅) = (6*5²+13*5+1) mod 17 = 12

Используя интерполяционную формулу Лагранжа, по которой пользователи могут восстановить полином, объединяя тени:

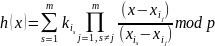
Получим секрет (j_s – номер пользователя):

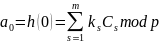
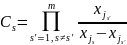
Используя тени 1, 2, 4, восстанавливаем секрет:

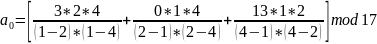
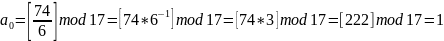
Восстановленный секрет k = 1.

Проверка:

h(x) = 6*x² + 13*x + 1

Секрет восстановлен верно.

Часть 2. Разделение сеансового ключа

Запустим программу «DivisonSecret», сгенерируем случайный секрет:

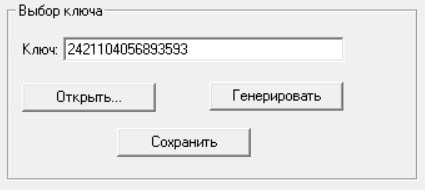
И зашифруем данным ключом произвольное сообщение алгоритмом DES:

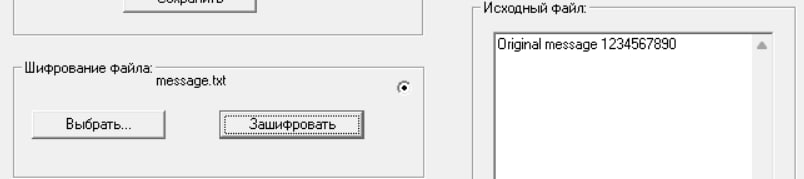
Получили криптограмму:

Далее, осуществим разделение секрета со следующими параметрами:

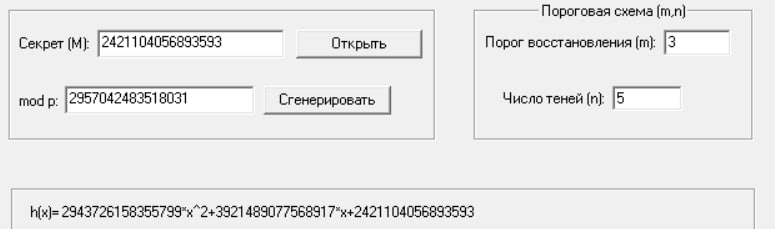
Получили следующие тени:

Восстановим секрет по теням, выбрав их произвольно. Пусть это будут тени 1, 3, 5:

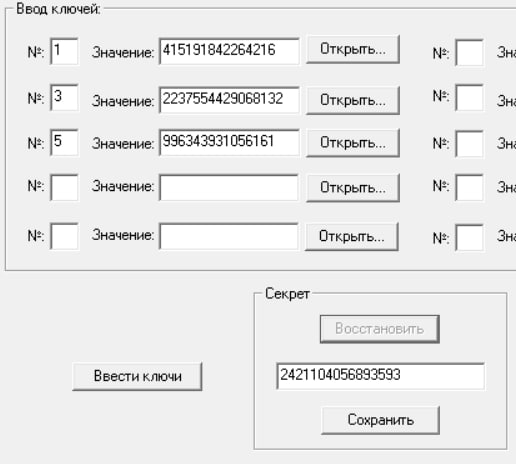
И с помощью восстановленного по теням секрета дешифруем криптограмму:

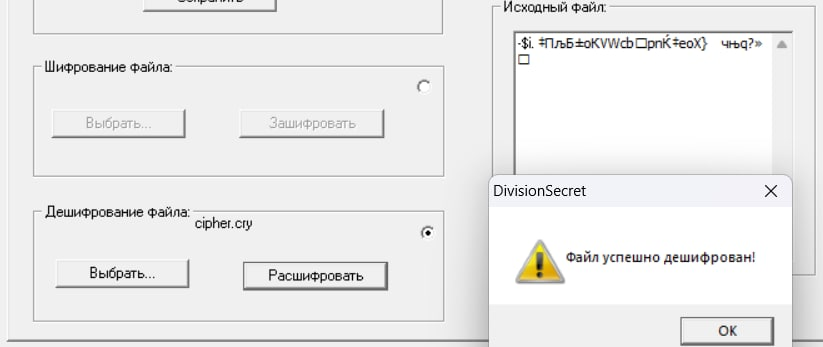
Расшифрованная криптограмма совпадает с исходным сообщением:

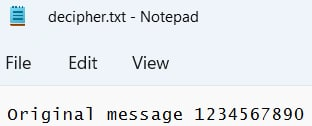
Изменим случайным образом одну из теней и восстановим секрет по новому набору теней:

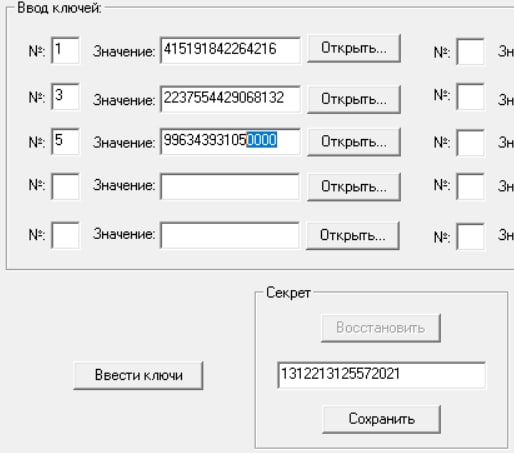
В тени №5 изменили последние 4 цифры на нули.

Попробуем снова дешифровать криптограмму вновь полученным секретом:

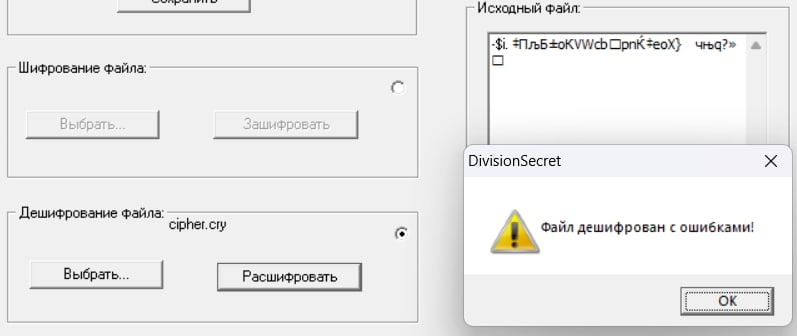
Как видим, дешифровать криптограмму секретом, восстановленным из неверно указанных теней, не удалось:

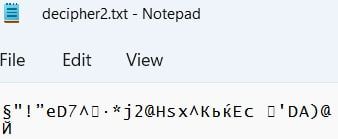
Вывод

В ходе выполнения лабораторной работы были закреплены знания по теме «протоколы разделения секрета». Была изучена схема разделения секрета на основе интерполяции полиномов над конечными полями (схема Шамира), а также применено разделение сеансового ключа для шифрования DES, с помощью программы «DivisionSecret».

Санкт-Петербург

2022