
0_practice_AIG_02_09
.pdfРешебник по АиГ
Учебное пособие
Казанский федеральный университет
2012

Оглавление
Глава 1. Вспомогательный материал . . . . . . . . . . . . . . . . . . . |
2 |
|
Ÿ 1. |
Комплексные числа . . . . . . . . . . . . . . . . . . . . . . . . . . . |
2 |
Ÿ 2. |
Многочлены . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
11 |
Ÿ 3. |
Определители второго и третьего порядков . . . . . . . . . . . . . |
14 |
Глава 2. Введение в аналитическую геометрию . . . . . . . . . . . . |
22 |
|
Ÿ 1. |
Векторная алгебра . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
22 |
Ÿ 2. |
Прямые на плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . |
32 |
Ÿ 3. |
Плоскости и прямые в пространстве . . . . . . . . . . . . . . . . . |
37 |
Глава 3. Системы линейных уравнений, матрицы, определители . |
46 |
|
Ÿ 1. |
Определители . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
46 |
Ÿ 2. |
Алгебра матриц . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
55 |
Ÿ 3. Метод Гаусса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
63 |
|
Глава 4. Векторные пространства . . . . . . . . . . . . . . . . . . . . . |
69 |
|
Ÿ 1. |
Линейные пространства . . . . . . . . . . . . . . . . . . . . . . . . . |
69 |
Ÿ 2. |
Линейная зависимость векторов . . . . . . . . . . . . . . . . . . . . |
79 |
Ÿ 3. |
Евклидовы пространства . . . . . . . . . . . . . . . . . . . . . . . . |
88 |
Ÿ 4. |
Ортогональные системы векторов. Матрица Грама . . . . . . . . . |
91 |
Ответы и указания . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
97 |
|

Глава 1
Вспомогательный материал
Ÿ1. Комплексные числа
1.Мнимой единицей называется такое число i, что i2 = ¡1. Пусть x, y вещественные числа. Число z = x + iy называется
комплексным числом. Число x называется действительной частью
комплексного числа, y мнимой частью.
Два комплексных числа z1 = x1 + iy1 è z2 = x2 + iy2 равны тогда и только тогда, когда равны их действительные и мнимые части, т. е.
x1 = x2; y1 = y2:
Число 0 + i0 называется нулем и обозначается символом 0.
Пусть z1 = x1 + iy1, z2 = x2 + iy2.
1) Сумма комплексных чисел z1 è z2 комплексное число
z= (x1 + x2) + i(y1 + y2):
2)Разность комплексных чисел z1 è z2 комплексное число
z= (x1 ¡ x2) + i(y1 ¡ y2):
3)Произведение комплексных чисел z1 è z2 комплексное число
z= (x1x2 ¡ y1y2) + i(x1y2 + x2y1):
4)При делении комплексного числа z1 íà z2 получается комплексное число
z = |
z1 |
= |
x1x2 + y1y2 |
+ i |
x2y1 ¡ x1y2 |
: |
|
z2 |
x22 + y22 |
x22 + y22 |
|||||
|
|
|
|
Пример. Найдем сумму, разность и произведение комплексных чисел z1 = 2 + i è z2 = 1 ¡ i:
z3 = z1 + z2 = 2 + i + 1 ¡ i = 3;
z4 = z1 ¡ z2 = 2 + i ¡ (1 ¡ i) = 1 + 2i;
z5 = z1z2 = (2 + i)(1 ¡ i) = 2 ¡ 2i + i ¡ i2 = 3 ¡ i:

Ÿ 1. Комплексные числа |
3 |
|
|
Заметим, что для чисел z1 = 2 + i è z2 = 1 ¡ i
x1 = 2; y1 = 1; x2 = 1; y2 = ¡1:
Подставляя эти выражения в формулу для частного, получим
z6 |
= |
z1 |
= |
2 + i |
= |
2 ¢ 1 + 1 ¢ (¡1) |
+ i |
1 ¢ 1 ¡ 2 ¢ (¡1) |
= |
1 |
+ i |
3 |
: |
||
|
|
|
|
|
|||||||||||
z2 |
1 ¡ i |
12 + (¡1)2 |
12 + (¡1)2 |
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|
||||||||
Число z¹ = x ¡ iy называется сопряженным к числу z = x + iy.
Заметим, что
zz¹ = (x + iy)(x ¡ iy) = x2 + y2:
Формула деления комплексных чисел получается, если умножить числитель и знаменатель на число, сопряженное к знаменателю.
Пример. Найти вещественные числа x; y, если
(2 ¡ i)x + (3 + 2i)y = 3 + 2i:
Расскроем скобки и приведем левую часть уравнения к виду a + ib, где a и b вещественные числа, получим
(2x + 3y) + i(¡x + 2y) = 3 + 2i:
Приравняем действительные и мнимые части чисел, стоящих в правой и левой частях этого равенства. Получим систему из двух урав-
нений:
2x + 3y = 3; ¡x + 2y = 2:
Решая ее методом исключения, найдем x = 0, y = 1.
Задания для самостоятельной работы
1.1. Найти вещественные числа x; y из уравнения
(1 + 2i)x + (3 ¡ 5i)y = 1 ¡ 3i:
1.2. Решить систему уравнений относительно комплексных чи-
ñåë z1, z2
(3 ¡ i)z1 + (4 + 2i)z2 = 2 + 6i; (4 + 2i)z1 ¡ (2 + 3i)z2 = 5 + 4i:
1.3.*1) Решить уравнение
z4 ¡ 3z2 + 4 = 0:
1)Символом ¾*¿ будем отмечать относительно более сложные задания

4 |
Глава 1. Вспомогательный материал |
|
|
Домашнее задание
1.4. Найти z1 + z2, z1 ¡ z2, z1z2, z1=z2, z¹1, z¹2, åñëè
z1 = 2 + 3i; z2 = 2 ¡ i:
1.5. Найти вещественные числа x; y; u; v из системы уравнений
(1 + i)x + (1 + 2i)y + (1 + 3i)u + (1 + 4i)v = 1 + 5i; (3 ¡ i)x + (4 ¡ 2i)y + (1 + i)u + 4iv = 2 ¡ i:
1.6. Решить систему уравнений относительно комплексных чи-
ñåë z1, z2
(2 + i)z1 + (2 ¡ i)z2 = 6; (3 + 2i)z1 + (3 ¡ 2i)z2 = 8:
1.7.* Решить уравнение
z4 + 2z2 ¡ 24z + 72 = 0:
2. Продолжим изучение алгебраических операций над комплекс-
ными числами.
p
Пример. Вычислим z = 2i. Будем искать решение в виде комплексного числа z = x + iy:
p
2i = x + iy:
Возведем обе части последнего равенства в квадрат, получим
2i = x2 + 2ixy ¡ y2:
Из условия равенства двух комплексных чисел получим систему двух уравнений
2xy = 2;
x2 ¡ y2 = 0:
Система решается методом подстановки. Из первого уравнения полу- чаем x = 1=y. Подставив это выражение во второе уравнение, полу- чим уравнение
y12 ¡ y2 = 0:
Таким образом, эта система имеет два решения
x = 1; y = 1 è x = ¡1; y = ¡1:
Отсюда первый корень z1 = 1 + i, второй корень z2 = ¡1 ¡ i.
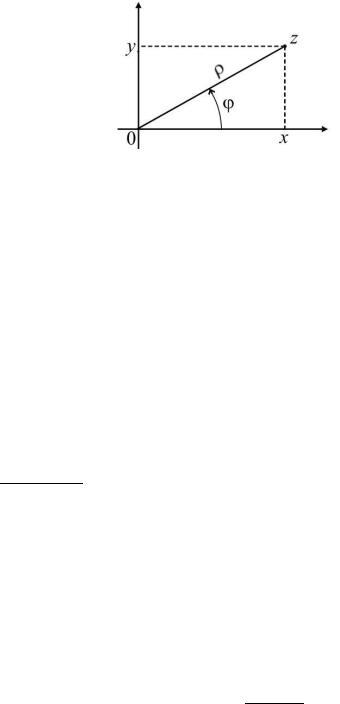
Ÿ 1. Комплексные числа |
5 |
|
|
Рис. 1. К тригонометрической форме комплексного числа.
Задания для самостоятельной работы
2.1. |
p |
|
|
p |
|
|
|
p |
|
|
(1 + i)8 |
|
|
|
|
|
|||||||||
Вычислить: a) |
¡8i, b) 3 ¡ 4i, c) |
¡15 + 8i, d) |
|
. |
||||||||
(1 ¡ i)6 |
||||||||||||
2.2. |
Привести выражение |
a + bi |
ê âèäó x + iy, ãäå a; b; x; y |
|||||||||
|
||||||||||||
вещественные числа. |
|
a ¡ bi |
|
|
|
|
|
|||||
2.3. |
Решить уравнение z2 ¡ (2 + i)z + (¡1 + 7i) = 0. |
|
|
|||||||||
Домашнее задание
2.4p. Вычисëèòü: a)p ¡3 ¡ 4i, b)p¡11 + 60i,
c) ¡8 + 6i,
d)(1 + i)9=(1 ¡ i)7.
2.5. Решить уравнение z2 ¡ (3 ¡ 2i)z + (5 ¡ 5i) = 0.
3. Любое комплексное число z = x + iy можно записать в тригонометрической форме
z = ½(cos ' + i sin ');
ãäå p
½ = jzj = x2 + y2
есть модуль комплексного числа, ' аргумент комплексного числа. Угол ' отсчитывается от положительного направления оси x против часовой стрелки (см. рис. 1) и изменяется от 0 до 2¼. Тогда
x = ½ cos '; y = ½ sin ':
Пример. Представить в тригонометрической форме числа a) z = 1 + i,

6 |
Глава 1. Вспомогательный материал |
|
|
b) z = ¡1 ¡ i.
Решение.
a) Пусть z = 1 + i. Найдем модуль этого числа
p |
|
|
|
|
p |
|
|
|
|
½ = x2 + y2 = 2: |
|
||||||||
Заметим, что |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
||||||
cos ' = p |
|
; |
sin ' = p |
|
; |
||||
2 |
2 |
||||||||
тогда аргумент ' = ¼=4, т. е. комплексное число z лежит в I четверти (сделайте рисунок!). Таким образом, тригонометрическое представление числа z будет
z= p2 ³cos ¼4 + i sin ¼4 ´:
b)Пусть z = ¡1 ¡ i. Модуль этого числа
pp
½ = x2 + y2 = 2:
Найдем аргумент. Заметим, что |
|
|
|
|
|
1 |
|
1 |
|
||
cos ' = ¡p |
|
; |
sin ' = ¡p |
|
; |
2 |
2 |
||||
тогда аргумент ' = 5¼=4, т. е. комплексное число лежит в III четверти (сделайте рисунок!). Таким образом, тригонометрическое представление числа z будет
z = p2 |
µcos |
54 |
+ i sin |
54 |
¶: |
|
|
|
|
¼ |
|
¼ |
|
Рассмотрим операции умножения, деления и возведения в степень комплексных чисел в тригонометрической форме. Пусть
z1 = ½1(cos '1 + i sin '1); z2 = ½2(cos '2 + i sin '2): |
|
||||
Тогда |
|
|
|
|
|
z1z2 = ½1½2(cos('1 + '2) + i sin('1 + '2)): |
|
||||
|
z1 |
½1 |
|
|
|
|
|
= |
|
(cos('1 ¡ '2) + i sin('1 ¡ '2)): |
|
|
z2 |
½2 |
|
||
|
|
zn = ½n(cos(n') + i sin(n')): |
(3.1) |
||
Формулу (3.1) называют формулой Муавра.

Ÿ 1. Комплексные числа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. Вычислим (1 + i)25. Обозначим z = 1 + i. Представим |
|||||||||||||||||||||||
число z в тригонометрическом виде |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
¼ |
|
|
|
|
|
¼ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
z = p2 |
³cos |
|
|
+ i sin cos |
|
|
|
´: |
|
||||||||||||
|
|
4 |
4 |
|
|||||||||||||||||||
Воспользуемся формулой Муавра, получим |
|
|
|
|
|
|
|
¶: |
|||||||||||||||
(1 + i)25 = z25 = p2 |
|
|
|
|
µcos 4 + i sin 4 |
||||||||||||||||||
|
|
|
|
|
|
|
25 |
25¼ |
|
|
25¼ |
|
|||||||||||
Упростим получившиеся выражение |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
¼ |
|
|
|
|
|
¼ |
|
|
|
|
|
p |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(1 + i)25 = 27p2 |
³cos |
|
+ i sin |
|
|
´ = 27p2 |
2 |
(1 + i) = 27 + 27i: |
|||||||||||||||
4 |
4 |
2 |
|||||||||||||||||||||
Таким образом, (1 + i)25 = 27 + 27i.
Пример. Доказать, что
(1 + cos ® + i sin ®)n = 2n cosn ®2 ³cos n®2 + i sin n®2 ´:
Представим единицу в тригонометрической форме, а затем используем формулы суммы синусов и косинусов:
(1 + cos ® + i sin ®)n = (cos 0 + i sin 0 + cos ® + i sin ®)n =
= ³2 cos2 |
2 + 2i sin 2 cos |
2 |
´ |
|
= 2n cosn |
2 |
³cos |
2 + i sin |
2 |
´: |
|||
|
® |
|
® |
|
® |
|
n |
|
® |
|
n® |
n® |
|
Напомним формулу бинома Ньютона: |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
Xk |
|
|
|
|
|
|
|
|
(a + b)n = |
Cnkan¡kbk; |
|
|
|
||||||
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
Cnk = |
n! |
; n! = 1 ¢ 2 ¢ : : : ¢ n; 0! = 1: |
|
|
||||||||
|
|
|
|
||||||||||
|
k! (n ¡ k)! |
|
|
||||||||||
Пример. Выразить cos 3x и sin 3x через cos x и sin x.
Пусть z = cos x + i sin x. Тогда z3 = cos 3x + i sin 3x. Следовательно, cos 3x = Re(z3), sin 3x = Im(z3). Расписав z3 с использованием бинома Ньютона и взяв вещественную и мнимую части, получим
cos 3x = 4 cos3 x ¡ 3 cos x;
sin 3x = 3 sin x ¡ 4 sin3 x:

8 Глава 1. Вспомогательный материал
Задания для самостоятельной работы
3.1. Представить в тригонометрической форме числа
a) i, p b) 1 + ip3, c) 2 ¡ i 3.
p
3.2. Вычислить выражение (1 ¡ i 3)(cos ' + i sin ').
2(1 ¡ i)(cos ' ¡ i sin ')
3.3.Описать множество точек, изображающих числа z, удовлетворяющих неравенствам:
à) jzj < 2,
b) jz ¡ ij · 1,
c) jz ¡ 1 ¡ ij < 1.
3.4.Вычислить (1 + i)6.
Домашнее задание
3.5. Представить в тригонометрической форме числа
a)¡1,
b)¡i,
c)¡1 + i,
d)1 ¡ i, p
e)¡1 + ip3,
f)¡1 ¡ i 3.
Ãp !20
3.6. |
|
1 + i |
3 |
|
Вычислить выражение |
|
|
. |
|
1 ¡ i |
|
|||
|
|
|
|
|
3.7.Найти min j3 + 2i ¡ zj, считая jzj · 1.
3.8.Вычислить ¡1=2 ¡ ip3=2¢5.
4. |
Корнями степени n из комплексного числа |
|
|
|||||||||||||
|
|
|
|
|
|
z = ½(cos ' + i sin ') |
|
|
|
|||||||
являются числа |
|
|
|
|
|
|
|
|
|
|
|
|
||||
z |
|
= pn |
|
(cos ' |
|
+ i sin ' |
); |
' |
|
= |
' |
+ |
2¼k |
; k = 0; 1; :::; n |
|
1: |
|
½ |
|
|
¡ |
||||||||||||
|
|
|
|
n |
||||||||||||
|
k |
|
|
|
k |
k |
|
|
k |
|
n |
|
|
|||
p
Пример. Извлечь корень 3 i.

Ÿ 1. Комплексные числа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пусть z = i. Представим z в тригонометрической форме |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
z = cos |
¼ |
|
+ i sin |
¼ |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
По формуле извлечения корня |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶; |
|
|
|||||||||||||||
zk = p3 z = p1 |
µcos |
3 |
|
|
+ i sin |
|
2 |
3 |
|
|
|
|
|
|
|
k = 0; 1; 2: |
||||||||||||||||||
|
|
3 |
|
|
¼=2 + 2¼k |
|
|
|
¼= |
|
|
+ 2¼k |
|
|
|
|
|
|||||||||||||||||
Выпишем все корни (сделайте рисунок!). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
¼ |
|
|
¼ |
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||
При k = 0 имеем z0 = cos |
|
|
+ i sin |
|
= |
|
|
|
+ i |
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||
|
6 |
6 |
2 |
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
||||||
При k = 1 имеем z1 = cos |
5¼ |
|
|
|
|
|
5¼ |
|
|
|
|
|
3 |
|
1 |
|
|
|||||||||||||||||
|
|
|
+ i sin |
|
|
= ¡ |
|
|
|
+ i |
|
|
. |
|
|
|||||||||||||||||||
6 |
|
6 |
|
2 |
|
2 |
|
|
||||||||||||||||||||||||||
При k = 2 имеем z2 = cos |
3¼ |
|
+ i sin |
3¼ |
|
= ¡i. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Напомним, что сумма первых n членов геометрической прогрес- |
||||||||||||||||||||||||||||||||||
сии вычисляется по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Sn = b + bq + bq2 + ::: + bq(n¡1) = b |
1 ¡ qn |
: |
(4.1) |
|||||||||||||||||||||||||||||
|
|
1 ¡ q |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример. Вычислить:
a)S1 = 1=2 + cos x + cos 2x + ::: + cos nx;
b)S2 = sin x + sin 2x + ::: + sin nx:
Положим S = S1 + iS2. Тогда Re(S) = S1, Im(S) = S2. Преобразуем сумму S, объединяя cos nx и sin nx при разных n:
S = 12 + (cos x + i sin x) + (cos 2x + i sin 2x) + ::: + (cos nx + i sin nx):
Используя (3.1) и (4.1), получим
S = 12 + (cos x + i sin x) + (cos x + i sin x)2 + ::: + (cos x + i sin x)n =
= |
1 |
|
+ |
(cos x + i sin x)(1 ¡ cos nx ¡ i sin nx) |
= |
|||
2 |
|
|
||||||
|
|
|
|
1 ¡ cos x ¡ i sin x |
|
|
||
= |
|
1 |
+ |
cos x ¡ (cos x cos nx ¡ sin x sin nx) |
+ |
|||
|
2 |
1 ¡ cos x ¡ i sin x |
||||||
|
|
|
|
|
|
|
||
+¡i(sin x cos nx + cos x sin nx) + i sin x = 1 ¡ cos x ¡ i sin x
