
0_practice_AIG_02_09
.pdf
10 |
Глава 1. Вспомогательный материал |
|
|
= |
1 |
+ |
cos x ¡ cos(n + 1)x ¡ i(sin(n + 1)x + i sin x |
: |
|
2 |
1 ¡ cos x ¡ i sin x |
||||
|
|
|
Умножим числитель и знаменатель второго слагаемого на сопряженное к знаменателю выражение и раскроем скобки. Имеем
S = 12+
+ |
[cos x + i sin x ¡ cos(n + 1)x ¡ i(sin(n + 1)x](1 ¡ cos x + i sin x) |
= |
|||||
|
|
1 |
|
(1 ¡ cos x)2 + sin2x |
|
|
|
= |
+ |
1 |
|
¢ |
|
||
2 |
1 ¡ 2 cos x + cos2x + sin2x |
|
|||||
¢[cos x ¡ cos2x + i sin x cos x ¡ cos(n + 1)x+
+ cos(n + 1)x cos x ¡ i sin x cos(n + 1)x + i sin x ¡ i sin x cos x ¡ sin2x¡ ¡i sin(n + 1)x + i sin(n + 1)x cos x + sin(n + 1)x sin x]:
Верн¼мся к вычислению S1: |
|
|||||
S1 = Re(S) = |
1 |
+ |
|
1 |
(cos x ¡ 1 ¡ cos(n + 1)x + cos nx) |
|
|
|
|
|
|||
2 |
2(1 |
¡ |
cos x) |
|||
|
|
|
|
|
|
|
Приведя слагаемые к общему знаменателю и применяя формулу для суммы косинусов, получим
S1 = |
1 ¡ cos x + cos x ¡ 1 ¡ (cos(n + 1)x + cos nx) |
= |
sin 2n2+1 x |
: |
|||||
2sinx |
|||||||||
|
|
4sin2 x |
|
|
|
|
|||
|
|
|
2 |
|
|
2 |
|
||
Аналогично для S2 имеем |
|
|
|
|
|
|
|
||
|
|
|
sin n+1 x sin nx |
|
|
|
|
||
|
S2 |
= |
2 |
2 |
: |
|
|
|
|
|
sin x |
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
Задания для самостоятельной работы
4.1p. Извлечь корни
a)p4 ¡4,
b)pn 1,
c)p3 1,
d)2 1.
4.2. Найти суммы
a)S1 = cos x + Cn1 cos 2x + ::: + Cnn cos(n + 1)x;
b)S2 = sin x + Cn1 sin 2x + ::: + Cnn sin(n + 1)x:

Ÿ 2. Многочлены |
11 |
|
|
Домашнее задание
s s s
|
|
p |
¡ i , b) 8 |
p |
|
|
p |
|
|
4.3. |
Вычислить a) |
6 1 |
1 |
|
+ i , c) 6 |
1 ¡ i |
|
. |
|
|
|
|
3 + i |
3 ¡ i |
1 + i 3 |
||||
p
4.4.Извлечь корень 5 2 + 3i.
4.5.Извлечь корни из единицы степени a) 6, b) 8.
4.6.Найти суммы
a) cos |
2¼ |
+ 2 cos |
4¼ |
+ ::: + (n |
¡ |
1) cos |
2(n ¡ 1)¼ |
; |
|||||
|
n |
|
n |
n |
|||||||||
|
|
|
|
|
|
|
|
||||||
b) sin |
2¼ |
+ 2 sin |
4¼ |
|
+ ::: + (n |
¡ |
1) sin |
2(n ¡ 1)¼ |
. |
|
|||
|
n |
|
n |
|
|
|
|||||||
|
|
|
|
|
|
|
n |
|
|||||
4.7. Решить уравнение (z + 1)m ¡ (z ¡ 1)m = 0.
Ÿ2. Многочлены
1.Многочленом называется функция вида
Pn(z) = anzn + an¡1zn¡1 + ::: + a1z + a0;
ãäå a0, a1, :::, an фиксированные комплексные числа, коэффициенты многочлена, n ¸ 0 степень многочлена.
Число b называется корнем многочлена, если Pn(b) = 0. Для проверки, является ли число b корнем многочлена, удобно пользоваться схемой Горнера. По теореме о делении многочленов для много- члена Pn(z) и многочлена Q1(z) = z ¡ b существуют два многочлена qn¡1(z) è r0 такие, что Pn(z) = (z ¡ b)qn¡1(z) + r0. Пусть
qn¡1(z) = cn¡1zn¡1 + cn¡2zn¡2 + ::: + c0; r0(z) = d0:
Воспользовавшись методом неопределенных коэффициентов, можно найти коэффициенты многочленов qn¡1(z) è r0(z) по следующей схеме:
|
an |
|
|
an1 |
an¡2 |
... |
|||
b |
cn¡1 = an |
cn¡2 = an¡1 + bcn¡1 |
cn¡3 = an2 + bcn¡2 |
... |
|||||
|
... |
|
a1 |
|
a0 |
|
|
||
|
|
|
|
||||||
... |
|
c0 = a1 + bc1 |
d0 = a0 + bc0 |
|
|
||||

12 |
Глава 1. Вспомогательный материал |
|
|
Åñëè d0 = 0, то число b будет являться корнем многочлена Pn(z). При поиске корней многочлена согласно теореме Вьета удобно в
качестве b сначала рассматривать числа вида pq , где p делители a0, а q делители an.
Пример. Найти вещественные корни многочлена
P5(z) = z5 ¡ 5z4 + 7z3 ¡ 2z2 + 4z ¡ 8:
Сначала проверим, являются ли корнями дроби вида pq . Выпишем
все делители свободного члена: §1; §2; §4; §8, делители старшего коэффициента §1. Тогда корнями уравнения уравнения могут быть числа: §1; §2; §4; §8. Воспользуемся схемой Горнера, проверим, какие из этих чисел являются корнями:
|
|
a5 = 1 |
|
a4 = ¡5 |
|
a3 = 7 |
|
|
a2 = ¡2 |
|
|
b |
c4 = a5 |
|
c3 = a4 + bc4 |
c2 = a3 + bc3 |
|
c1 = a2 + bc2 |
|||
|
1 |
1 |
-4 |
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡1 |
1 |
6 |
|
13 |
|
|
-15 |
|
|
|
2 |
1 |
-3 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 = 4 |
|
a0 = ¡8 |
|
|
|
|
|
|
|
|
c0 = bc1 + a1 |
d0 = bc0 + a0 |
|
|
|
||
|
|
|
|
5 |
|
-3 |
|
|
|
|
|
|
|
|
19 |
|
-27 |
|
|
|
|
|
|
|
|
4 |
|
0 |
|
|
|
|
Из таблицы видно, что P5(z) |
= (z ¡ 2)(z4 |
¡ 3z3 + z2 + 4). |
||||||||
Для поиска оставшихся корней удобно восользоваться многочленом q4(z) = (z4 ¡ 3z3 + z2 + 4). Потенциальные корни этого многочлена §1; §2; §4. Числа §1 можно не проверять, т.к. они не являются корнями исходного многочлена P5(z). Проверим остальные числа:
|
|
|
|
|
|
|
|
1 |
|
|
-3 |
|
1 |
|
|
0 |
4 |
|
|
|||||||
|
|
|
|
|
2 |
|
1 |
|
-1 |
-1 |
-2 |
0 |
|
|
||||||||||||
Получили q |
|
( |
z |
z |
|
2)(z3 |
¡ |
z2 |
¡ |
z |
¡ |
2). Продолжим поиск корней |
||||||||||||||
|
4 |
|
) = ( 3¡ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
§1; §2. |
|||||||||
у многочлена q3 |
(z) = z |
¡ z |
|
|
¡ z ¡ 2. Потенциальные корни2 |
|||||||||||||||||||||
Воспользовавшись схемой Горнера, получим q3(z) = (z¡2)(z |
+z+1). |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
-1 |
|
-1 |
|
|
-2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
1 |
|
|
1 |
|
1 |
|
|
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Ÿ 2. Многочлены |
13 |
|
|
Можно заметить, что у многочлена z2 +z+1 вещественных корней нет. Таким образом, многочлен P5(z) имеет корень 2 кратности три, и его можно представить в виде P5(z) = (z ¡ 2)3(z2 + z + 1).
Пример. Для того, чтобы найти все (в том числе и комплексные) корни многочлена
P5(z) = z5 ¡ 5z4 + 7z3 ¡ 2z2 + 4z ¡ 8;
необходимо решить квадратное уравнение
z2 + z + 1 = 0:
Решения этого уравнения комплексные числа
p z = ¡12 § i 23:
Занумеруем все кони многочлена P5 с учетом их кратности: p
z1;2;3 = 2; z4;5 = ¡ |
1 |
§ i |
3 |
: |
|
|
|||
2 |
2 |
Многочлен P5 можно представить теперь в виде
P5(z) = (z ¡ 2)3 |
Ãz + 2 + i |
23!Ãz + |
2 ¡ i |
23! |
: |
||||||||
|
|
1 |
|
p |
|
|
1 |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задания для самостоятельной работы
1.1.Найти корни многочлена z5 + 7z4 + 16z3 + 8z2 ¡ 16z ¡ 16.
1.2.Определить кратные множители многочленов:
a)z6 ¡ 6z4 ¡ 4z3 + 9z2 + 12z + 4,
b)z6 ¡ 15z4 + 8z3 + 51z2 ¡ 72z + 27.
1.3. Разложить на неприводимые вещественные множители мно-
гочлены:
a) z4 + 4,
b) z4 ¡ az2 + 1; ¡2 < a < 2.
1.4. Определить ¸ так, чтобы один из корней уравнения
z3 ¡ 7z + ¸ = 0
равнялся удвоенному другому.
14 |
Глава 1. Вспомогательный материал |
|
|
1.5. |
Когда z3m ¡ z3n+1 + z3p+2 делится на z2 ¡ z + 1? |
Домашнее задание
1.6.Определить кратные множители многочленов: a) z5 ¡ 10z3 ¡ 20z2 ¡ 15z ¡ 4,
b) z5 ¡ 6z4 + 16z3 ¡ 24z2 + 20z ¡ 8.
1.7.Разложить не неприводимые вещественные множители мно-
гочлены:
a)z6 + 27,
b)z4 + 4z3 + 4z2 + 1.
1.8. Сумма двух корней уравнения 2z3 ¡z2 ¡7z + ¸ = 0 равна 1. Определить ¸.
Ÿ3. Определители второго и третьего порядков
1.Рассмотрим систему двух уравнений с двумя неизвестными
a11x1 + a12x2 |
= b1 |
; |
(1.1) |
|
a21x1 + a22x2 = b2: |
||||
|
||||
Здесь a11, a12, a21, a22, b1, b2 заданные, вообще говоря, комплексные числа, x1, x2 требуется найти. Таблицу
µ¶
A = |
a11 |
a12 |
|
a21 |
a22 |
||
|
называют матрицей второго порядка. Величину
¢ = a11a22 ¡ a12a21
называют определителем матрицы A. Для определителя используют также следующие обозначения:
¯
det(A) = jAj = ¯¯¯ a11
a21
¯
a12 ¯¯¯ = ¢:
a22
Åñëè ¢ =6 0, òî x1 è x2 можно найти по формулам Крамера:
|
|
|
x1 |
= |
¢1 |
|
; x2 = |
¢2 |
; |
|
|
|
||||
|
|
|
|
¢ |
|
|
¢ |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
ãäå |
= |
¯ |
b2 |
a22 |
¯ |
; ¢2 = |
¯ |
a21 |
b2 |
¯ |
: |
|||||
¢1 |
||||||||||||||||
|
|
¯ |
b1 |
a12 |
¯ |
|
¯ |
a11 |
b1 |
¯ |
|
|||||
|
|
¯ |
¯ |
|
¯ |
¯ |
|
|||||||||
|
|
¯ |
|
|
|
|
¯ |
|
¯ |
|
|
|
¯ |
|
||

Ÿ 3. Определители второго и третьего порядков |
15 |
|
|
Эти формулы не имеют смысла, когда
jAj = a11a22 ¡ a12a21 = 0;
èëè |
a11 |
|
a12 |
|
||
|
= |
; |
||||
|
|
|
|
|
||
|
a21 |
a22 |
||||
|
|
|
||||
т. е. строки определителя jAj пропорциональны. Если при этом и
b1 = a12 ;
b2 a22
то первое и второе уравнения системы (1.1), фактически, совпадают, и она имеет бесконечное множество решений. Если jAj = 0, но
b1 6= a12 ;
b2 a22
то первое и второе уравнения системы (1.1) противоречивы, система несовместна, не имеет ни одного решения.
Примеры. 1) Определитель матрицы системы
x1 + 2x2 = 5; 3x1 + 4x2 = 6;
равен |
|
|
|
|
¢ = |
¯3 4¯ |
= 4 ¡ 6 = ¡2: |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
¯ |
1 |
2 |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
Система имеет единственное¯ |
решение¯ |
¯3 6¯ |
|
|
|
|
|
|
|||||||||||||||||
x1 = |
¯6 4¯ |
20 |
¡ |
12 |
= 4; x2 = |
6 |
¡ |
15 |
9 |
|
|||||||||||||||
¯ |
5 |
2 |
¯ |
= |
|
|
|
|
¯ |
1 |
5 |
¯ |
= |
|
|
= : |
|||||||||
|
¯1 2¯ |
|
|
|
2 |
|
|
|
¡ |
|
¯1 2¯ |
|
|
|
2 |
2 |
|
||||||||
|
¯ |
|
|
¯ |
¡ |
|
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
¡ |
|
|
|
||
|
¯3 |
4¯ |
|
|
|
|
|
|
|
|
|
|
|
¯3 |
4¯ |
|
|
|
|
|
|
||||
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
2) Определитель матрицы системы
x1 + 2x2 = 3; 2x1 + 4x2 = 6;
равен |
¯2 4¯ |
= 4 ¡ 4 = 0: |
|||
¢ = |
|||||
|
¯ |
1 |
2 |
¯ |
|
|
¯ |
|
|
¯ |
|
|
¯ |
|
|
¯ |
|
16 |
Глава 1. Вспомогательный материал |
|
|
Рис. 2. Правило расстановки знаков в определителе третьего порядка
Ïðè ýòîì
b1 |
= |
a12 |
= |
3 |
= |
2 |
: |
|
b2 |
a22 |
6 |
4 |
|||||
|
|
|
|
Уравнения системы, фактически, совпадают. Система имеет бесчисленное множество решений.
3) Система
x1 + 2x2 = 2; 2x1 + 4x2 = 6;
не имеет решений, так как ее определитель равен нулю, но
b1 6= a12 :
b2 a22
Обратимся к системе трех уравнений с тремя неизвестными
a11x1 a21x1 a31x1
+a12x2
+a22x2
+a32x2
+a13x3
+a23x3
+a33x3
= b1;
= b2; (1.2)
= b3:
Из ее коэффициентов можно составить матрицу третьего порядка
A = |
0 a21 |
a22 |
a23 |
1: |
|
a11 |
a12 |
a13 |
A |
|
@ a31 |
a32 |
a33 |
Определитель этой матрицы вычисляется по формуле
¢= a11a22a33 + a12a23a31 + a13a21a32¡
¡a13a22a31 ¡ a12a21a33 ¡ a11a23a32:
Для запоминания знаков, с которыми слагаемые входят в эту сумму,
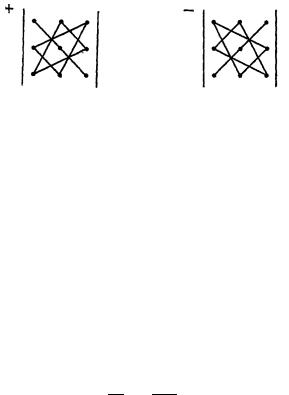
полезно использовать схему, представленную на рисунке 2. |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Пример |
|
5 |
|
9 + 2 |
|
6 |
|
7 + 3 |
|
4 |
|
8 |
|
3 |
|
5 |
|
7 |
|
4 |
|
2 |
|
9 |
|
1 |
|
8 |
|
6 = |
|||
¯4 5 |
6¯ |
= 1 |
¢ |
¢ |
¢ |
¢ |
¢ |
¢ |
¡ |
¢ |
¢ |
¡ |
¢ |
¢ |
¡ |
¢ |
¢ |
||||||||||||||||||
¯7 8 |
9¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
¯ |
1 |
2 |
3 |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Ÿ 3. Определители второго и третьего порядков |
17 |
|
|
= 45 + 84 + 96 ¡ 105 ¡ 72 ¡ 48 = 225 ¡ 225 = 0:
Если ¢ =6 0, то единственное решение системы (1.2) можно найти по формулам Крамера:
|
|
|
|
|
|
xi = |
¢i |
; |
i = 1; 2; 3; |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ãäå |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢1 = |
¯ |
b2 |
a22 |
a23 |
¯ |
; ¢2 = |
¯ |
a21 b2 |
a23 |
¯ |
; ¢3 |
= |
¯ |
a21 |
a22 |
b2 |
¯ |
: |
||
|
¯ |
b3 |
a32 |
a33 |
¯ |
|
¯ |
a31 |
b3 |
a33 |
¯ |
|
|
¯ |
a31 |
a32 |
b3 |
¯ |
|
|
|
¯ |
b1 |
a12 |
a13 |
¯ |
|
¯ |
a11 |
b1 |
a13 |
¯ |
|
|
¯ |
a11 |
a12 |
b1 |
¯ |
|
|
|
¯ |
|
|
|
¯ |
|
¯ |
|
|
|
|
¯ |
|
|
¯ |
|
|
|
¯ |
|
|
¯ |
|
|
|
¯ |
|
¯ |
|
|
|
|
¯ |
|
|
¯ |
|
|
|
¯ |
|
|
¯ |
|
|
|
¯ |
|
¯ |
|
|
|
|
¯ |
|
|
¯ |
|
|
|
¯ |
|
a)
d)
f)
Задания для самостоятельной работы
1.1. Вычислить определители второго порядка: |
|
|
|||||||||||||||||||||||
¯ |
3 4 |
¯ |
; b) |
¯ |
8 5 |
¯ |
; c) |
¯ |
|
|
a + b |
|
|
¡a ¡ b |
|
||||||||||
¯ |
1 2 |
¯ |
|
|
|
¯ |
3 2 |
¯ |
|
¯ |
a2 + ab + b2 a2 |
|
|
ab + b2 |
|||||||||||
¯ |
sin ®¯ |
cos ® |
¯ |
e) |
¯cos ' +¯i sin ' |
|
|
1 |
|
|
|
|
|
; |
|||||||||||
¯ |
sin ¯ |
¯ |
cos ¯ |
¯; |
¯ |
|
¯ |
|
|
|
|
|
cos ' ¡ i sin ' |
¯ |
|||||||||||
¯ |
|
¯ |
|
¯ |
|
|
1 |
|
|
|
|
|
|
||||||||||||
¯ |
|
|
|
|
|
¯ |
|
¯ |
|
|
|
(1 |
|
t) |
2 |
|
2t |
|
|
|
|
¯ |
|
||
¯ |
|
|
|
|
|
¯ |
|
¯ |
|
|
|
|
|
|
|
|
|
|
¯ |
|
|||||
¯ |
x ¡3 1 |
|
|
|
¯ |
|
¯ |
|
|
¯ |
|
|
¡ |
|
|
|
|
|
|
|
¯ |
¯ |
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|||||||||
|
x |
2 |
|
1 |
|
|
; g) |
1 + t |
|
|
1 + t |
|
|
: |
|
||||||||||
¯ |
x |
|
|
+ x + 1 |
¯ |
|
|
¯ |
|
|
2t |
|
|
|
|
(1 + t) |
2 ¯ |
|
|
||||||
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
¯ |
|
|
|||||||
¯ |
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
¡ |
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
¯ |
|
|
¯ |
1 + t |
|
|
1 + t |
|
¯ |
|
|
||||||
¯ |
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
¯
¯
¯¯;
1.2. Решить систему уравнений методом Крамера.
a)
b)
5x ¡ 7y |
= |
1; |
|
|
|
|
|
|
|
|
|
x ¡ 2y |
= |
0: |
|
|
|
¼ |
|
|
|
||
x cos ® ¡ y sin ® |
= |
cos ¯; |
ãäå ® = |
+ k¼; k |
2 |
N: |
|||||
= |
sin ¯; |
|
2 |
||||||||
x sin ® + y cos ® |
6 |
|
|
||||||||
1.3. Исследовать, будет ли система уравнений определенной (имеет единственное решение), неопределенной (имеет бесконечно много решений) или несовместной (не имеет решения):
ax + 4y = 2;
9x + ay = 3:
18 |
|
|
|
|
|
|
|
|
|
|
Глава 1. Вспомогательный материал |
|||
|
|
|
|
|||||||||||
|
1.4. Вычислить определители третьего порядка: |
¯ |
|
|||||||||||
a) |
¯ |
4 |
1 |
¡2 |
¯ |
; |
b) ¯ |
¡ |
sin ® cos ® cos ¯ |
cos ® sin ¯ |
; |
|||
|
¯ |
5 |
2 |
¡3 |
¯ |
|
¯ |
0 |
|
sin ¯ |
cos ¯ |
¯ |
|
|
|
¯ |
3 |
2 |
4 |
¯ |
|
¯ |
cos ® |
sin ® cos ¯ |
sin ® sin ¯ |
¯ |
|
||
|
|
|
¡ |
|
|
|
¡ |
|
|
|
||||
|
¯ |
|
|
|
¯ |
|
¯ |
|
|
|
|
|
¯ |
|
|
¯ |
1 |
i |
1¯ |
+ i |
¯ |
|
|
|
|
|
¯ |
|
|
c) |
¯¯ |
1¡ |
i |
1 |
¯ |
0 |
¯: ¯ |
|
|
|
|
|
¯ |
|
|
¯ |
i |
0 |
|
1 |
¯ |
|
|
|
|
|
|
|
|
|
¯ |
¡ |
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
¯1:5: Решить систему¯ |
уравнений методом Крамера: |
|
|||||||||||
|
|
2x + 3y + 5z = 10; |
|
4x ¡ 3y + 2z + 4 = 0; |
|
|
||||||||
a) 3x + 7y + 4z = 3; b) 6x ¡ 2y + 3z + 1 = 0; |
|
|
||||||||||||
|
|
x + 2y + 2z = 3; |
|
5x ¡ 3y + 2z + 3 = 0: |
|
|
||||||||
1:6:¤ Доказать, что если все элементы определителя третьего порядка равны §1, то сам определитель будет четным числом.
|
Домашнее задание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
a) |
1:7: Вычислить определители второго порядка: |
d) |
¯ |
1 |
|||||||||||||||||||||||||
¯ |
8 |
12 |
¯; |
b) ¯ |
ab |
|
b2 |
¯; |
c) ¯ |
sin ® |
|
¡cos ® |
¯ |
; |
|||||||||||||||
|
¯ |
6 |
9 |
¯ |
|
|
¯ |
a2 |
ab |
¯ |
|
|
|
¯ |
cos ® |
|
|
|
sin ® |
¯ |
|
|
¯ |
tan ® |
|||||
|
¯ |
" 1¯ |
|
|
¯ |
|
|
|
¯¼ |
|
|
|
¯ |
|
¼ |
|
|
|
|
|
¯ |
|
|
¯ |
|
||||
e) |
¯ |
¡1 " |
¯ |
; |
ãäå¯ " = cos¯ |
|
+ i sin¯ |
|
: |
|
|
|
|
¯ |
|
|
¯ |
|
|||||||||||
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
¯ |
¯ |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯1:8: Решить¯ |
систему уравнений методом Крамера: |
|
|
|||||||||||||||||||||||||
a) |
2x ¡ 3y = 4; |
|
|
b) |
|
4x + 7y + 13 = 0; |
|
|
|
|
|
||||||||||||||||||
|
4x ¡ 5y |
= |
10; |
|
|
|
5x + 8y + 14 |
= |
0: |
|
|
|
|
|
|||||||||||||||
|
1:9: Вычислить определители третьего порядка: |
|
¯ |
|
|||||||||||||||||||||||||
a) |
¯ |
2 |
5 |
3 |
¯ |
; |
b) |
¯ |
3 |
¡2 |
8 |
¯ |
; |
|
c) |
¯ |
sin ¯ |
cos ¯ |
1 |
; |
|||||||||
|
¯ |
3 |
4 |
2 |
¯ |
|
|
¯ |
1 |
¡7 |
|
|
5 |
¯ |
|
|
|
¯ |
sin ° |
cos ° |
1 |
¯ |
|
||||||
|
¯ |
3 |
2 |
1 |
¯ |
|
|
¯ |
4 |
|
3 |
5 |
¯ |
|
|
|
¯ |
sin ® |
cos ® |
1 |
¯ |
|
|||||||
|
|
|
|
|
|
|
¡ |
|
¡ |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
¯ |
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
¯ |
|
|
|
¯ |
|
|
|
|
|
¯ |
|
||
|
¯ |
1 |
1 |
1¯ |
|
|
¯ |
|
|
|
|
|
|
|
¯ |
|
|
|
¯ |
|
|
|
|
|
¯ |
|
|||
|
¯ |
|
|
|
¯ |
|
|
¯ |
|
|
|
|
2¼¯ |
|
|
|
¯2¼ |
|
|
|
|
¯ |
|
||||||
d) |
¯ |
1 |
! |
! |
¯; |
ãäå ! = cos |
|
|
|
+ i sin |
|
|
|
: |
|
|
|
|
|
||||||||||
|
3 |
|
|
3 |
|
|
|
|
|
||||||||||||||||||||
|
¯ |
1 |
!2 |
! |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
¯ |
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯1:10: Ïðè¯каком условии справедливо равенство |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
¯ |
cos ® |
|
1 |
|
cos ° |
¯ = |
¯ |
cos ® |
0 |
|
cos ° |
¯? |
||||||||||||
|
|
|
|
|
¯ |
cos ¯ |
cos ° |
|
|
1 |
|
|
¯ |
|
|
¯ |
cos ¯ |
cos ° |
0 |
¯ |
|
||||||||
|
|
|
|
|
¯ |
1 |
|
cos ® |
cos ¯ |
¯ |
|
|
¯ |
0 |
|
|
cos ® |
cos ¯ |
¯ |
|
|||||||||
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
|
¯ |
|
¯
¡1 ¯¯¯; tan ®
Ÿ 3. Определители второго и третьего порядков |
|
19 |
|||
|
|||||
1:11: Решить систему уравнений методом Крамера: |
|||||
5x ¡ 6y + 4z = 3; |
5x + 2y + 3z + 2 = 0; |
||||
a) 3x ¡ 3y + 2z |
= |
2; |
b) 2x ¡ 2y + 5z |
= |
0; |
4x ¡ 5y + 2z |
= |
1: |
3x + 4y + 2z + 10 = |
0: |
|
1:12:¤ Найти наибольшее значение, которое может принимать определитель третьего порядка, при условии, что все его элементы равны §1.
2.Укажем свойства определителей третьего порядка.
1)Если транспонировать матрицу (то есть поменять ролями строки и столбцы), то е¼ определитель не изменится.
2)Если все элементы какой-либо строки равны нулю, то определитель тоже равен нулю.
3)Если все элементы какой-либо строки умножить на одно и то же число, то и весь определитель умножится на это число.
4)Если поменять местами две строки определителя, то определитель изменит свой знак на противоположный.
5)Если две строки определителя совпадают, то определитель равен нулю.
6)Если все элементы одной строки пропорциональны соответствующим элементам другой строки, то определитель равен нулю.
7)Если каждый элемент некоторой строки определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все прочие строки прежние, а в заданной строке в первом определителе стоят первые, а во втором вторые слагаемые, например,
¯ |
a |
a31 |
|
a32 |
|
a33 |
|
¯ |
|
11a21 |
11 |
12a22 |
12 |
13a23 |
13 |
¯ |
|
||||||
¯ |
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
¯ |
= |
¯ |
a21 |
¯ |
|
¯ |
a31 |
¯ |
|
¯ |
a11 |
¯ |
|
¯ |
|
¯ |
|
¯ |
|
¯ |
|
¯ |
|
a22 |
a23 |
¯+¯ |
a21 |
|
a32 |
a33 |
¯ |
¯ |
a31 |
a12 |
a13 |
¯ |
¯ |
b11 |
|
|
¯ |
¯ |
|
|
|
¯ |
¯ |
|
|
|
¯ |
¯ |
|
¯
b12 b13 ¯¯ a22 a23 ¯¯: a32 a33 ¯
8)Если к элементам одной строки определителя прибавить соответствующие элементы другой строки, предварительно умноженные на некоторое число, определитель не изменится.
9)Если некоторая строка определителя является линейной комбинацией других строк, то определитель равен нулю.
