
- •Resumen
- •Abstract
- •Índice
- •Índice de figuras
- •Índice de tablas
- •Descripción y funcionamiento de ciclos Rankine regenerativos
- •Funcionamiento básico del ciclo Rankine
- •Ciclos Rankine regenerativos
- •Configuración de estudio
- •Operación de ciclos Rankine a carga parcial
- •Rendimiento de ciclos Rankine
- •Descripción del funcionamiento de turbinas de vapor
- •Control de turbinas de vapor
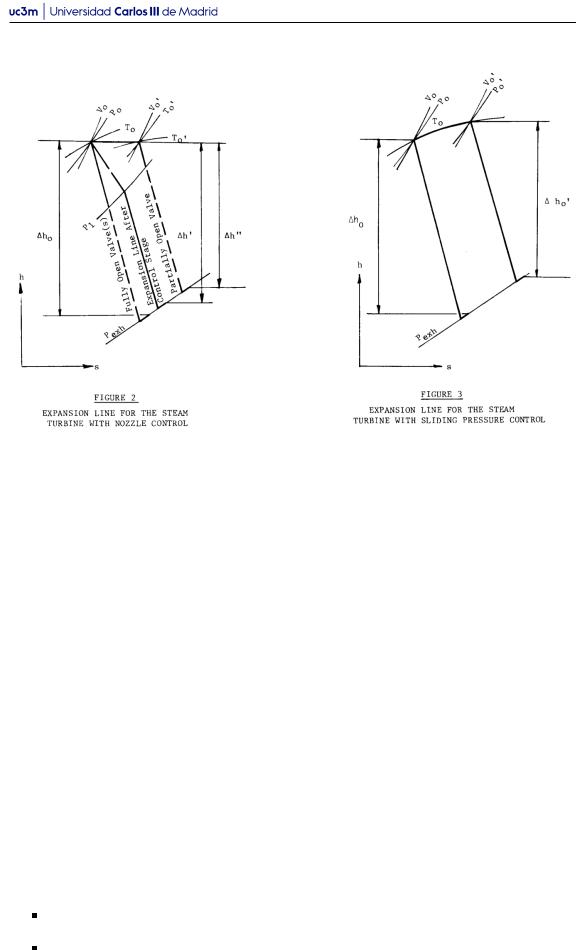
- •Operación en presión deslizante y presión constante
- •Metodología de cálculo del rendimiento isentrópico a carga parcial de turbinas de vapor
- •Rendimiento isentrópico a carga parcial de la turbina de alta presión
- •Cálculo de la línea de expansión de la turbina de alta presión
- •Rendimiento isentrópico a carga parcial de las turbinas de media y baja presión
- •Corrección de Baumann para etapas con condensación
- •Línea de expansión de las turbinas de media y baja presión
- •Corrección al punto final de la línea de expansión en la turbina de baja presión
- •Perdidas de escape y entalpía real utilizada (UEEP)
- •Rendimiento isentrópico base y rendimiento isentrópico en condiciones de diseño
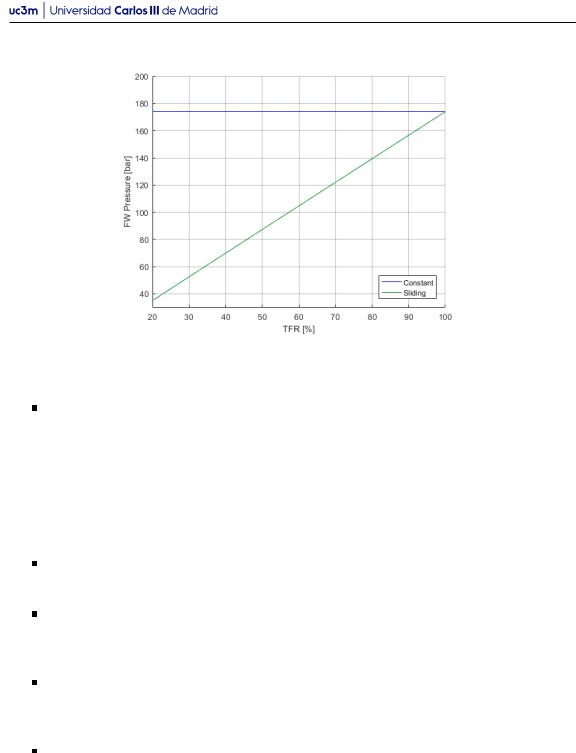
- •Calculo de presión de funcionamiento mediante la ley de Stodola
- •Fugas de vapor a través de los sellos
- •Modelización de los calentadores cerrados
- •Funcionamiento de los calentadores cerrados
- •Cálculo del flujo másico de extracción
- •Dimensionado de calentadores cerrados
- •Parámetros geométricos iniciales
- •Coeficiente de convección del agua de alimentación y resistencia de conducción del tubo
- •Coeficiente global de transferencia de calor del desuperheater
- •Coeficiente global de transferencia de calor del condensador
- •Coeficiente global de transferencia de calor del subcooler
- •Cálculo de calentadores cerrados a carga parcial
- •Modelización de otros componentes del ciclo Rankine
- •Generador de vapor
- •Cálculo de la extracción del desaireador
- •Operación de las bombas de alimentación y condensado
- •Modelo simplificado de operación del condensador a carga parcial
- •Resolución de ciclos Rankine a carga parcial, y en condiciones de diseño
- •Obtención de las condiciones de diseño
- •Resolución del balance de calor del tren de calentadores
- •Diagrama de flujo del proceso cálculo
- •Calidad de solución, desviación y residuos
- •Análisis de resultados y validación
- •Rendimiento del ciclo a carga parcial
- •Resumen de resultados en presión deslizante y presión constante
- •Diagrama T-s del ciclo
- •Rendimiento a carga parcial de turbinas de vapor
- •Influencia de cada corrección
- •Lineas de expansión a carga parcial
- •Operación del tren de calentadores
- •Calentadores fuera de servicio o en bypass
- •Cierre manual de válvulas
- •Coeficiente de transferencia de calor a carga parcial
- •Validación de los resultados
- •Uso del programa
- •Entrada de datos
- •Visualización de resultados
- •Conclusiones
- •Bibliografía
Félix Ignacio Pérez Cicala
(a) Línea de expansión a presión constante |
(b) Línea de expansión a presión deslizante |
Figura 2.7: Líneas de expansión de turbinas de vapor [10]
2.2.Metodología de cálculo del rendimiento isentrópico a carga parcial de turbinas de vapor
El método de Spencer, Cotton y Cannon [1] consiste en utilizar una serie de curvas, obtenidas de forma empírica, para determinar la variación del rendimiento isentrópico al cambiar parámetros de operación.
Las curvas se pueden utilizar de forma grá ca o mediante la forma polinómica de las mismas. La forma polinómica se puede implementar de forma relativamente sencilla en un programa de cálculo. En el programa de cálculo desarrollado, se dispone de una función única que utiliza como parámetros la gura deseada y el valor de la variable independiente de la curva para obtener la variación del rendimiento isentrópico correspondiente.
El método de cálculo consiste en multiplicar de forma sucesiva los valores obtenidos con las curvas a un rendimiento isentrópico base de la turbina, de acuerdo a la ecuación (2.4). El rendimiento base es un parámetro propio del modelo de turbina, y sería el primer parámetro a cambiar para utilizar el método con modelos de turbinas modernos o distintos a los utilizados en [1].
isen = isen base (1 + %=100) |
(2.4) |
Donde:
isen es el rendimiento isentrópico de la etapa.
isen base es el rendimiento isentrópico base de la turbina.
Modelización de ciclos Rankine mediante el método |
25 |
de Spencer, Cotton y Cannon |
|
Félix Ignacio Pérez Cicala
Figura 2.8: Presión a la salida del generador de vapor
% es la variación porcentual obtenida de la curva.
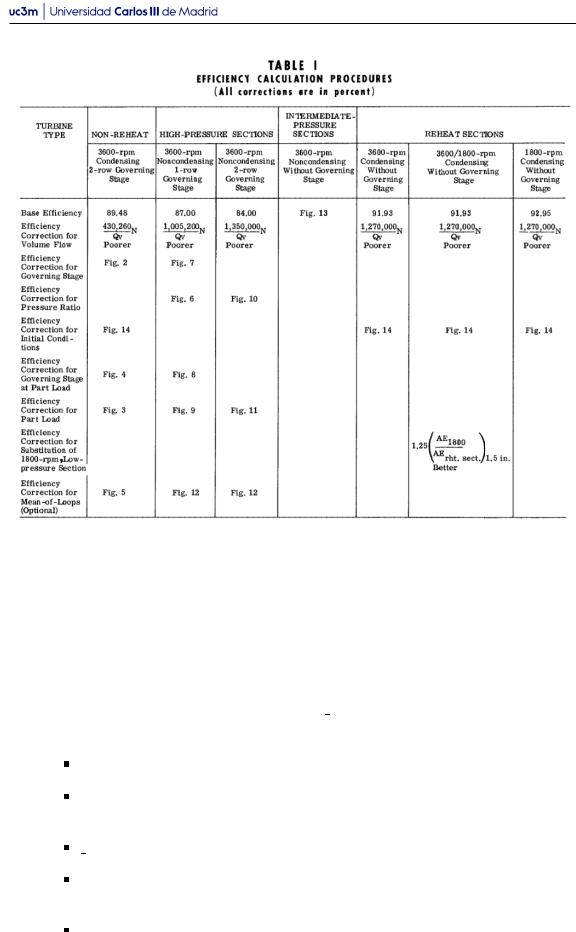
La metodología presentada en el método de Spencer, Cotton y Cannon [1] es aplicable a distintos tipos de turbina, siguiendo los pasos de la Tabla 2.1. En este proyecto se han implementado los tipos de turbina correspondientes a turbinas de alta presión (”High pressure sections”), y a turbinas con recalentamiento (”Reheat sections”). Los dos tipos de turbina utilizados en el ejemplo de cálculo presentado en [1] forman parte de este subgrupo. Cada tipo de turbina implementado se corresponde a una columna de la Tabla 2.1, que son:
”3600-rpm Noncondensing 1-row Governing Stage”: Turbina de alta presión, utilizada en el ejemplo de cálculo.
”3600-rpm Noncondensing 2-row Governing Stage”: Opción para turbina de alta presión. Su rendimiento base es menor que la turbina de alta presión con etapa de gobierno de unala, pero su rendimiento a carga parcial es mejor.
”3600-rpm Noncondensing Condensing without Governing Stage”: Turbina de media y baja presión acoplada al eje de 3600 rpm de la turbina de alta presión, utilizada en centrales modernas.
”3600/1800-rpm Noncondensing Condensing without Governing Stage”: Turbinas de media y baja presión, utilizada en el ejemplo de cálculo. También llamadas ”Cross-compound”, se utilizaban con frecuencia en centrales antiguas.
2.2.1. Rendimiento isentrópico a carga parcial de la turbina de alta presión
El método de cálculo parte de un rendimiento insentrópico base de la turbina de alta presión, dependiente del modelo de turbina. En el método de Spencer, Cotton y Cannon [1], el rendimiento isentrópico base es del 87 % para la turbina de alta presión con etapa de gobierno de una la, pero este valor cambiaría para modelos distintos o turbinas modernas.
Modelización de ciclos Rankine mediante el método |
26 |
de Spencer, Cotton y Cannon |
|
Félix Ignacio Pérez Cicala
Tabla 2.1: Pasos de cálculo para distintos tipos de turbina [1]
A continuación se enumeran las distintas correcciones que se deben hacer para obtener el rendimiento isentrópico nal, para la turbina del ejemplo de cálculo presentado en [1] (es decir, ”3600-rpm Noncondensing 1-row Governing Stage”).
1. Corrección de e ciencia por caudal volumétrico. |
|
|
|
|
|
|
% = |
1005200 cu |
N |
(2.5) |
|||
|
|
|
|
|||
m |
|
|
||||
|
|
|
|
|
|
|
Donde:
% es la variación porcentual del rendimiento isentrópico, aplicada según (2.4).
cu es un cambio de unidades para pasar de lb/hr y cuft/lb a m3/s (cambio a sistema internacional), de valor cu = 0;0283168=3600.
m es el caudal másico en condiciones de diseño en kg/s.
es el volumen especí co en condiciones de diseño a la entrada de la turbina, en m3/kg.
N es el número de secciones de ujo en paralelo al principio de la expansión, para el caso de estudio de valor 1.
Modelización de ciclos Rankine mediante el método |
27 |
de Spencer, Cotton y Cannon |
|
Félix Ignacio Pérez Cicala
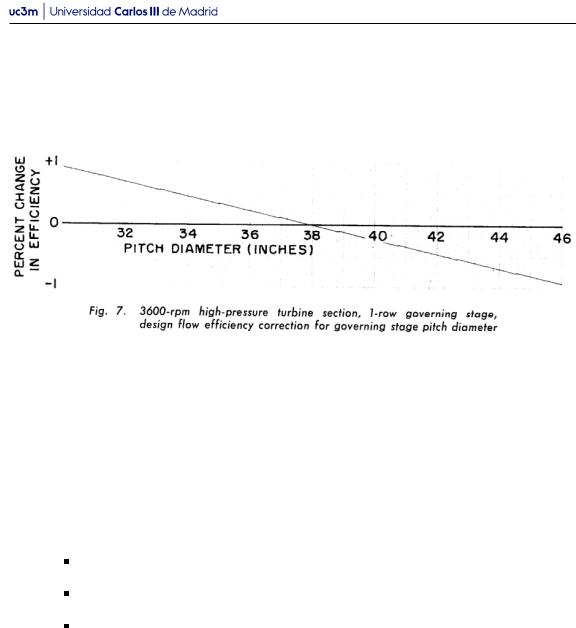
2.Corrección de e ciencia por diámetro de etapa de gobierno. En la Figura 2.9, se muestra la curva según se presenta en el método de Spencer, Cotton y Cannon [1]. La corrección depende únicamente del diámetro de la etapa de gobierno, y su valor se aplica al rendimiento base según la ecuación (2.4).
Figura 2.9: Corrección por diámetro de etapa de gobierno [1]
3.Corrección por ratio de presión. Se aplica obteniendo el valor con la Figura 2.10, y la corrección al rendimiento base usando la ecuación (2.4). Se elige una curva según el caudal volumétrico en condiciones de diseño, y se obtiene el valor de la corrección calculando el ratio de presión según la ecuación (2.6).
Pratio = |
Pout; diseno~ |
(2.6) |
|
Pin; throttle |
|||
|
|
Donde:
es el ratio de presión.
es la presión de salida en condiciones de diseño.
Pin; throttle es la presión en la entrada antes de la válvula de control (throttle valve), en condiciones de diseño.
4.Corrección por diámetro etapa de gobierno en carga parcial. En función del TFR (Throttle Flow Ratio), de nido según la ecuación (2.3), se puede calcular la corrección del rendimiento isentrópico, y se aplica según la ecuación (2.6). La representación grá ca correspondiente a esta corrección se muestra en la Figura 2.11.
5.Corrección de e ciencia por operación a carga parcial. Esta corrección depende del ratio de presión de la turbina en condiciones de diseño y del TFR, de nido según la ecuación (2.3). Es la corrección de mayor peso en el valor nal del rendimiento isentrópico en cargas bajas. En la Figura 2.12, se muestra la representación grá ca correspondiente a la corrección. El valor obtenido se aplica al rendimiento base según la ecuación (2.6). En el programa, esta corrección no se aplica en presión deslizante, de acuerdo a lo explicado en la Subsección 2.1.2.
6.La última corrección que aparece en la Tabla 2.1 es opcional y no se utiliza en el programa desarrollado.
Modelización de ciclos Rankine mediante el método |
28 |
de Spencer, Cotton y Cannon |
|
