Félix Ignacio Pérez Cicala
1.Con el ujo másico de cálculo ( ujo másico de agua de alimentación para el cual se desea resolver el ciclo a carga parcial), y las condiciones de diseño, comenzar el proceso, construyendo las matrices de la (5.1) con las entalpías en condiciones de diseño.
2.Calcular el ujo másico de las extracciones mediante la ecuación (5.1).
3.Resolver en primer lugar las presiones de cada etapa de la turbina (de acuerdo a la Sección 2.3), y a continuación el rendimiento isentrópico según la Sección 2.2. Calcular la línea de expansión de la turbina de alta presión en modo de presión constante.
4.Recalcular las temperaturas de salida del tren de calentadores, utilizando el proceso descrito en la Sección 3.4. También se recalcula en este paso la operación de las bombas.
5.Con las nuevas entalpías de salida obtenidas en los pasos anterior, reconstruir la matriz de entalpías y el vector de términos independientes de la ecuación (5.1).
6.Calcular la desviación y residuos de la iteración, según la Sección 5.4. Si se alcanzan las tolerancias deseadas, detener el proceso iterativo y calcular parámetros nales. Si aún no se han alcanzado, repetir el proceso iterativo desde el paso 2, utilizando las nuevas matrices de entalpías calculadas.
Si al nal de la iteración se alcanza la tolerancia de desviación y residuos deseada, se naliza el proceso iterativo y se calcula la potencia generada por el ciclo. Si no se ha alcanzado la tolerancia, se vuelve a repetir el proceso, empezando por recalcular el ujo másico de las extracciones utilizando las entalpías calculadas en la iteración anterior.
5.4. Calidad de solución, desviación y residuos
El criterio para detener el proceso iterativo consiste en medir dos parámetros, los cuales son indicativos de la calidad de solución alcanzada. Estos dos parámetros son la desviación y los residuos, y cuando se alcanzan los valores deseados para cada parámetro se detiene el proceso iterativo.
La desviación consiste en calcular la diferencia en el valor para un parámetro cualquier entre iteraciones. Cuando la desviación se acerca a valores muy pequeños, signi ca que la solución no está cambiando signi cativamente entre iteraciones. En el programa desarrollado se controla la desviación de multitud de parámetros, pertenecientes a la turbina, calentadores, bombas y parámetros globales del ciclo. El valor nal de la desviación es el máximo de todos los evaluados. La desviación se calcula de forma proporcional a la magnitud del parámetro estudiado, de acuerdo a la ecuación (5.4).
dev = |
vi vi 1 |
(5.4) |
vi
Donde:
dev es el valor de la desviación para el parámetro que se está evaluando.
vi es el valor del parámetro en la iteración actual. vi 1 es el valor del parámetro en la iteración anterior.
Modelización de ciclos Rankine mediante el método |
64 |
de Spencer, Cotton y Cannon |
|
Félix Ignacio Pérez Cicala
Los residuos de cálculo aparecen al resolver ecuaciones mediante procesos iterativos, y son producto de haber resuelto la ecuación con unos coe cientes determinados que luego se vuelven a calcular y cambian. En el programa se controlan los residuos de dos maneras distintas:
En la resolución de los calentadores, se utilizan funciones propias de Matlab, que devuelven soluciones respetando una tolerancia determinada.
En la resolución del ujo másico de las extracciones de acuerdo a la ecuación (5.1), se calculan los residuos de acuerdo a la ecuación (5.5). Estos residuos son los que se muestran al usuario por pantalla.
Los residuos de la ecuación (5.1) se calculan según la ecuación (5.5). Durante el proceso de cálculo descrito en la Figura 5.1, se calculan en primer lugar los ujos másicos de las extracciones (usando los valores de entalpías de la iteración anterior), y con los valores nuevos de los ujos másicos se resuelve el tren de calentadores obteniendo nuevos valores de las entalpías. Los residuos se calculan con los ujos másicos utilizados para obtener las entalpías nuevas, y miden por tanto la calidad de la solución a la ecuación (5.1).
res = h i mex i 1 |
mfw h i |
(5.5) |
Donde:
res es el valor de los residuos para la ecuación.
h es la matriz de variación de entalpías correspondientes a extracciones, calculada en la iteración actual.
mex i 1 es el ujo másico de extracciones, calculado en la iteración anterior y utilizado para calcular las entalpías de la iteración actual.
mfw h es el vector de términos independientes, calculado utilizando entalpías de la
i
iteración actual.
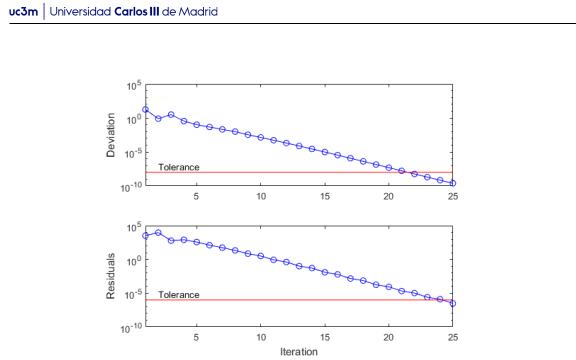
En la Figura 5.2 se muestra la evolución de la desviación y residuos de una solución, con escala vertical logarítmica. Se puede observar que se alcanza la solución en 25 iteraciones, con tolerancia de desviación de 10 8 y tolerancia de residuos de 10 6, y que se alcanzó antes la tolerancia de desviación que la residuos. Esto a pesar de que la tolerancia de desviación era más restrictiva.
En la Tabla 5.1 se muestran los valores por defecto para los parámetros que controlan el proceso iterativo, y para el factor de amortiguamiento según se de ne en la (5.3). Estos valores pueden cambiarse con la interfaz del programa.
Parámetro |
Valor |
Máximo número de iteraciones |
300 |
Tolerancia de desviación |
1e-8 |
Tolerancia de residuos |
1e-6 |
Factor de amortiguamiento |
0.3 |
Tabla 5.1: Valores por defecto para proceso iterativo
Modelización de ciclos Rankine mediante el método |
65 |
de Spencer, Cotton y Cannon |
|
Félix Ignacio Pérez Cicala
Figura 5.2: Desviación y residuos de solución segun aparecen en el programa
Modelización de ciclos Rankine mediante el método |
66 |
de Spencer, Cotton y Cannon |
|