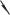студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

В теории случайных процессов эта функция называется

функцией корреляции, а в оптике — временной´ функцией когерентности случайного процесса 2 , описывающего хаоти-

ческий характер световых колебаний (хаотические изменения амплитуды и фазы ).

Как мы увидим в дальнейшем, она определяет результат

интерференции квазимонохроматических волн и является количественной мерой корреляции (когерентности), качественные

представления о которой были введены при обсуждении статистической природы светового излучения.

Используя определение (7.22), найдем

1 2

Определение > включает в себя следующую последовательность операций: нужно взять значение 7 в момент времени и умножить на значение функции 7 в момент времени>. Перебираем всевозможные значения (при фиксиро-

2. Найдя их среднее, получим значение функции > при заданном фиксированном значении >.

Мы полагаем, что от положения интервала усреднения

на оси времени функция не зависит, т. е. световое излучение представляет собой стационарный случайный процесс. Это

означает, что физические (макроскопические) параметры, определяющие свойства источника излучения (температура, давление и т. д.), а также условия на пути распространения света от источника к точке наблюдения остаются неизменными во времени.

Исследуем характер поведения функции > . При > 0 функция > равна интенсивности света

тельных чисел 7 7 2 , т. е. изображающие отдельные колебания вектора на векторной диаграмме выстроены коллинеарно вдоль действительной оси. Ясно, что суммарный вектор 0 имеет при этом максимально возможную длину. Таким образом, функция > имеет при > 0 максимально возможное значение, равное интенсивности света. Как изменяется это значение с ростом >? Ясно, что пока > >0 —

Итак, > 0, аналогичным образом >

При > >0 значения фаз и > некоррелированы, т. е. при заданном фаза > может с равной вероятностью принимать любые значения от нуля до 2$, следовательно и разность фаз > может быть любой, принимая с равной вероятностью (за время наблюдения >0) все

возможные значения. Величина D оказывается близкой к нулю.

7.4 ] Функция когерентности 543

Таким образом,

> 7 7 > D# 0 при > >0

Итак, введенная нами функция > имеет «правильное поведение», которое соответствует нашим качественным представлениям о сильной корреляции при > >0 (при этом > :0D# ) и об отсутствии корреляции при > >0 (при этом> 0). Функция > и является количественной мерой коррелированности значений случайного процесса 2 в два момента времени разделенных промежутком >.

Подчеркнем, что в результате усреднения мы получаем детерминированную функцию > , которая является одной из

важнейших характеристик стационарного случайного процесса 7 . Эта функция определяет закон, по которому постепенно уменьшается когерентность с ростом >.

Удобно, наряду с (7.22), ввести нормированную функцию

которая изменяется от единицы при > 0 до нуля при > >0. Функцию 5 > называют комплексной степенью когерентности случайного процесса 2 .

Понятие временн´ой когерентности, введенное выше для слу-

чайного колебательного процесса 2 , можно обобщить, введя

функцию взаимной когерентности двух случайных процессов

21 и 22 :

7.5. Интерференция квазимонохроматических волн

Пусть колебание в некоторой точке наблюдения создано суперпозицией двух квазимонохроматических волн -1 и -2 вида (7.15). Тогда суммарный колебательный процесс в этой точке имеет вид

- -1 -2

Регистрируемая приемником света интенсивность, согласно (7.21), есть

: -2 2 ,

где — амплитуда результирующего колебания - . Результирующий колебательный процесс представляет собой хаотически модулированное колебание с медленно меняющимися (в масштабе периода 0 2$ 0) амплитудой и фазой

- 0

Ясно, что поскольку в слагаемых колебаниях амплитуды1 и 2 , а также фазы 1 и 2 сохраняются неизмен-

с тем, что квазигармонические колебания можно складывать по правилу сложения векторов так же, как строго гармонические колебания (рис. 7.12).

7.5 ] Интерференция квазимонохроматических волн 545

Используя теорему косинусов, получаем

где 1 2 .

Проводя усреднение последнего равенства в интервале времени регистрации (которое, напомним, много больше времени когерентности), находим

: 2 — интенсивность результирующего колебания. Используя комплексные представления (7.16) и (7.17), легко

получить

Третье слагаемое в (7.26) можно теперь представить, используя (7.28) в виде

2 1 2 2 Re 21 22

Итак,

Последняя формула представляет собой наиболее общее выражение, справедливое для любой двухлучевой интерференционной схемы. Наибольший интерес представляет интерференци-

онное слагаемое 2 Re 21 22 . Именно с ним связано отличие суммарной интенсивности : от суммы интенсивностей :1 :2, т. е. интерференционный эффект.

Первый важный вывод, который можно сделать из (7.29), состоит в том, что некогерентные волны не могут интерфериро-

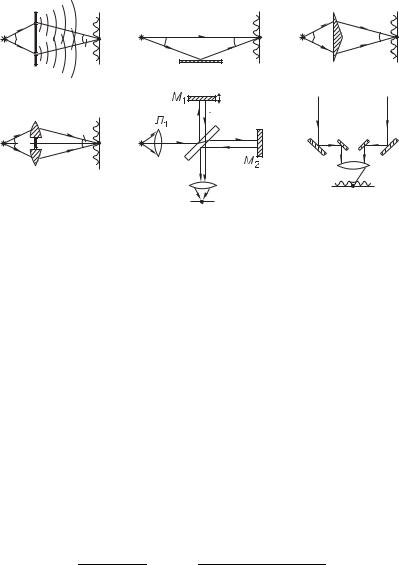
вать. Действительно, при 21 22 0 мы имеем : :1 :2, т. е. при наложении некогерентных волн имеет место закон сложения интенсивностей. В частности, если волны 21 и 22 испущены независимыми источниками, то они некогерентны и не могут давать интерференционных эффектов. Интерференция может наблюдаться лишь в том случае, если волны по крайней мере частично когерентны. Поэтому в интерференционных схемах всегда используют один источник света, а две (или несколько) интерферирующих волн получают путем деления (расщепления) одной волны, излучаемой источником. На рис. 7.13 приведены примеры нескольких интерференционных схем, широко применяемых в оптике: а — опыт Юнга, б — схема Ллойда, в — бипризма Френеля, г — билинза Бийе, д — интерферометр Майкельсона, е — звездный интерферометр Майкельсона: лучи 1 и 2 идут от удаленного источника. Во всех схемах излучение источника 9

18 Основы физики. Т. I

548 Интерференция волн [ Гл. 7

3. Если > >0, то 5 > 1 и вместо (7.34) получаем

: > 2:0 1 > ,

где > — временное запаздывание, — разность хода. Точно такое же выражение получается, если рассматривать строго гармонические волны. Мы получили, таким образом, ответ на вопрос о применимости синусоидальной идеализации: при сложении когерентных волн все происходит так, как если бы волны были строго гармоническими.

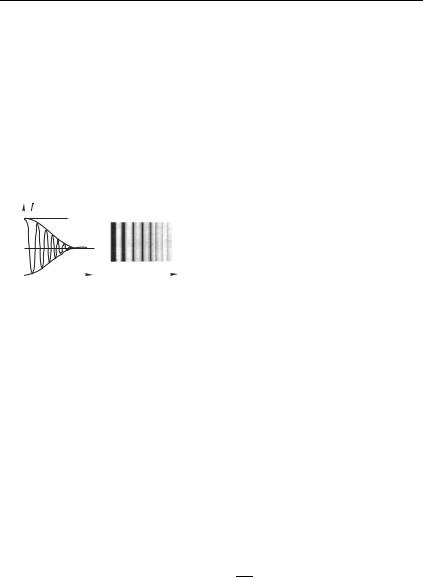
Общий характер зависимости интенсивности в интерференционной картине от > (т. е. при изменении положения

0> > (его значение меняется от 1 до 0 при изменении > на 0 2) «промодулирован» медленно спадающей функцией5 > ( 5 > спадает от единицы до нуля при изменении > от нуля до >0), т. е. мы наблюдаем множество переходов от светлой полосы к темной (т. е. множество интерференционных полос) прежде, чем они окончательно исчезнут.

Разумеется, точный ход зависимости : > определяется конкретным видом функции 5 > , т. е. в конечном счете свойствами источника, от которого зависит форма цугов излучения. Рисунок 7.14 дает качественное представление об этой зависимости, достаточное, впрочем, для проведения некоторых оценок. Можно

заключить, что максимальная разность хода, при которой еще видна интерференция >0, а максимальный порядок интерференции

7.0 .0

Величину >0 принято называть длиной цуга (это пространственная протяженность цуга излучения длительности >0).

Таким образом, максимально допустимая разность хода ограничена длиной цуга, максимальный порядок интерференции — числом периодов колебаний, содержащихся в цуге излучения:

>0 0.

7.6 ] Связь функции когерентности и распределения энергии 549

7.6. Связь функции когерентности и распределения энергии по спектру. Соотношение неопределенностей

Изучая распределение интенсивности в интерференционной картине, можно определить функцию когерентности квазимонохроматической волны, излучаемой тепловым источником света — таков вывод из выражения (7.34).

С другой стороны, о свойствах излучения можно судить по спектральным измерениям, исследуя с помощью спектрального прибора распределение энергии по спектру квазимонохроматической волны в фиксированной точке наблюдения. Важно понять, в каком соотношении находятся эти способы измерения, какова связь между функцией когерентности и энергетическим спектром?

Распределение энергии по спектру квазимонохроматического колебания можно

определить например с помо- щью призменного спектрографа S (рис. 7.15).

Параллельный пучок квазимонохроматического света пада-

ет на призму и, благодаря дисперсии — зависимости показателя преломления от частоты, разделяется на множество монохроматических пучков, каждый с определенной частотой . Интенсив-

ность каждого из этих пучков , определяющую распределение энергии по частоте, называют спектральной интенсив-

ностью. Сумма интенсивностей всех монохроматических пучков равна, очевидно, интенсивности квазимонохроматического света, попадающего на входную щель спектрографа:

Смысл соотношения (7.35) состоит в том, что полная интенсивность света может быть получена путем аддитивного сложения интенсивностей отдельных монохроматических волн, состав-

ляющих суммарную квазимонохроматическую волну: другими словами, спектральные гармоники разных частот некогерент-

ны между собой. Следовательно, интерференционная картина, получаемая с помощью источника квазимонохроматического излучения, может быть рассчитана следующим образом: нужно взять отдельную монохроматическую компоненту частоты (и интенсивности ) и найти интерференционную картину, создаваемую этой компонентой, используя формулу (7.8)

550 Интерференция волн [ Гл. 7

после чего некогерентно сложить вклады:

Очевидно, результаты расчетов, основанные на спектральном подходе (формула (7.37)) и временном подходе (формула (7.33)) должны быть тождественными. Исходя из этого, мы можем связать спектральную интенсивность с функцией временной когерентности > .

Наиболее важной является связь между шириной спектра(интервалом частот, в котором спектральная интенсивностьзаметно отличается от нуля) и временем когерентности >0 (интервал значений >, в котором отлична от нуля функция когерентности > ).

Рассмотрим простой пример. Пусть функция имеет вид

где :0 0 — интенсивность интерферирующих волн (т. е. суммарная интенсивность всех спектральных компонент).

Функция изображена на рис. 7.17. Здесь быстро изменяющийся множитель 0 промодулирован медленным

множителем 27 (так как 0). Максимально до-

27