
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf3.2 ] |
Ангармонический осциллятор |
461 |
вмоменты скачкообразного уменьшения индуктивности (поток
+: сохраняется!). Сделав полный оборот по фазовой траектории, изображающая точка попадает в ту же начальную точку на плоскости / / (т. е. значения / и / через период колебаний восстанавливаются).
Мы рассматривали вопрос параметрической раскачки уже имеющихся малых колебаний. Но почему вообще возникают колебания? Ведь вначале маятник или колебательный контур находятся в покое. Откуда берется эта «начальная затравка»? Здесь принципиальную роль играют флуктуации. В частности, тепловое хаотическое движение зарядов в колебательном контуре приводит к хаотическим малым колебаниям, которые всегда существуют в контуре — это и есть та «затравка», которая далее параметрически раскачивается до наступления стационарного режима.
Отметим в заключение, что параметрические методы используются не только в механических или электрических системах. В настоящее время подобные методы используются даже для генерации световых колебаний (параметрические лазеры).
3.2. Ангармонический осциллятор
До сих пор мы изучали поведение колебательных систем, совершающих малые колебания; мы рассматривали малые отклонения системы от положения равновесия, когда «силу», возвращающую систему к положению равновесия, можно приближенно считать пропорциональной величине смещения. При этом уравнение, описывающее колебательную систему, является линейным, колебание — гармоническим, а период колебаний не
зависит от амплитуды (это свойство гармонического осциллятора называют изохронностью).
В случае не малого отклонения от положения равновесия уравнение, описывающее процесс колебаний, оказывается в общем случае нелинейным, колебательный процесс уже не является гармоническим, а система теряет свойство изохронности: период колебаний оказывается зависящим от амплитуды (т. е. от величины начального отклонения и (или) начальной скорости).
Рассмотрим в качестве примера математический маятник. Если угол отклонения маятника от положения равновесия не полагать малым, то уравнение, описывающее процесс колебания, нелинейно (см. § 2.1):
2 |
|
0 |
(3.6) |
# 0 |
# |
Исследование нелинейных систем (и, в частности, системы, описываемой уравнением (3.6)) представляет собой чрезвычайно
462 Параметрические колебания. Ангармонический осциллятор [ Гл. 3
сложную математическую проблему, которая далеко выходит за рамки этой книги. Мы рассмотрим, не прибегая к сложным математическим методам, лишь одну проблему: зависимость периода колебаний от амплитуды. При этом мы ограничимся приближе-
нием |
3 |
|
|
# # 6 , |
(3.7) |
учтя лишь первую поправку к выражению # # (которое приводит к уравнению гармонического осциллятора и независимости периода колебаний от амплитуды).
Понятно, что учет слагаемого #3 6 приводит к уменьшению величины возвращающей силы: 7 # # #3 6 по срав-
|
|
|
|
|
|
нению с линейной зависимостью 7 # |
|
|
|
|
|
|
#; следовательно к уменьшению уско- |
|
|
|
|
|
|
|
|
|
|
|
|
|
рения и скорости, а значит — к росту пери- |
|
|
|
|
|
|
ода колебаний при увеличении амплитуды. |
|
|
0 |
|
|
|
Пусть максимальное отклонение маятни- |
|
|
|
|
|
||
|
|
|
||||
H0 |
|
|
|
H |
ка от положения равновесия (амплитуда ко- |
|
|
|
|
||||
|
||||||
|
|
|
||||
|
H |
|
|
|
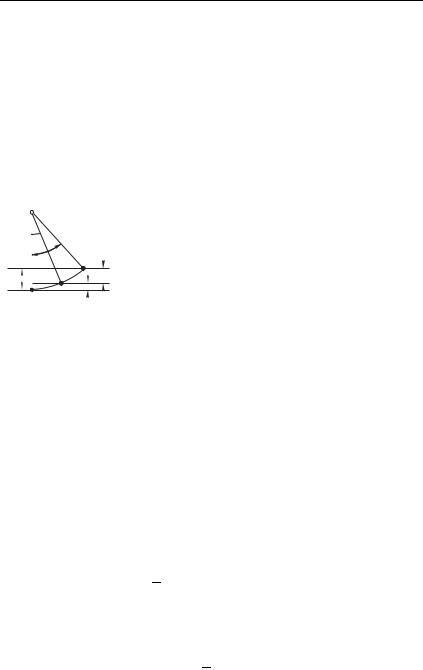
лебаний) равна #0. Из закона сохранения |
|
|
|
|
|
|
||
|
|
|
|
|
энергии |
|
|
|
|
|
|
|
|
|
|
Рис. 3.3 |
2 G |
|||
|
|
|
|
|
|
2 |
(см. рис. 3.3) находим скорость маятника в момент, когда его отклонение равно #:
|
2 G |
, где G G0 G 2 2 |
0 |
|
2 (3.8) |
||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
||||
Если за время |
угол поворота маятника равен , а длина |
||||||||||||||||||||||||||
пройденного за это время пути |
|
, то |
|
|
|||||||||||||||||||||||
или, используя (3.8), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.9) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 2 0 2 2 2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
Интегрирование этого выражения в пределах от 0 до #0 дает |
|||||||||||||||||||||||||||
четверть периода колебаний 4, поэтому |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
'0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 0 2 2 2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||
При использовании |
линейного |
приближения |
# # мы |
||||||||||||||||||||||||
получили бы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
4 |
|
|
, |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||

3.2 ] |
Ангармонический осциллятор |
463 |
где # #0. Нет надобности вычислять этот интеграл: результат известен — ведь линейное приближение приводит к уравнению гармонического осциллятора, период колебаний которого
0 2$ , поэтому
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.10) |
|
|
|
|
2 |
||||
|
|
|
|||||
|
1 2 |
||||||
0 |
|
|
|
|
|
||
Не приводя подробных (хотя и очевидных) преобразований, запишем выражение для периода , которое получается при использовании приближения (3.7) (т. е. первой нелинейной поправки)
|
|
|
|
1 |
|
|
|
|
1 |
#2 |
1 |
1 2 |
|
|||
4 |
|
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 2 |
|
6 |
0 |
1 2 |
|
|||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
Первое слагаемое — это период колебаний гармонического осциллятора (т. е. период малых колебаний маятника). Второе слагаемое — поправка, приводящая к увеличению периода, если амплитуда не слишком мала.
Относительная величина поправки 0 равна
|
2 |
1 |
1 |
2 |
|
|
|
|
|
0 |
|
|
|
|
(3.11) |
||
|
24 |
|
|
|
|
|||
0 |
1 2 |
|
||||||
|
|
0 |
|
|
|
|
|
|
Важно подчеркнуть, что поправка пропорциональна квадрату амплитуды колебаний.
Мы не будем вычислять интеграл, входящий в оценку (3.11). Очевидно, что подынтегральная функция в (3.11) ни при каком не превышает подынтегральную функцию в (3.10) более
чем вдвое (на интервале от |
|
|
|
|
|
|
|
|
|
нуля до единицы), поэтому и |
f |
|
|
f |
|
|
|||
|
|
||||||||
величина интеграла менее чем |
|
|
|
|
|
|
|
|
|
вдвое отличается от $ 2, т. е. |
|
|
x |
|
|
x |
|||
|
2 |
|
|
|
|
||||
0 |
' #0 $ 24 . Более |
|
|
|
|
|
|
|
|
|
|
O |
|
|
O |
||||
точные |
вычисления приводят |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
к оценке 0 1 16 #02. |
|
|
|
|
|
|
|
|
|
Подобная ситуация возни- |
|
|
|
|
|
|
|
|
|
à |
|
á |
|
||||||
кает и в пружинном маятни- |
|
|
|||||||
|
|
|
|
|
|
|
|
||
ке, если жесткость пружины уменьшается при увеличении
деформации. График на рис. 3.4 a соответствует именно этому случаю: жесткость пружины 7 уменьшается с ростом (такую характеристику принято называть мягкой). В слу-
464 Параметрические колебания. Ангармонический осциллятор |
[ Гл. 3 |
чае жесткой характеристики (рис. 3.4 б) 7 |
растет |
при увеличении деформации — в этом случае рост амплитуды приводит к уменьшению периода колебаний.
Колебательный контур, в катушку индуктивности которого вставлен железный сердечник, также представляет собой ангармонический осциллятор: при больших амплитудах (большом токе через катушку) индуктивность + начинает зависеть от величины тока, при этом магнитный поток через катушку + : : уже не является линейной функцией величины тока. Отклонение от линейности обычно описывается функцией
: +0 +1 3, (3.12)
где константы +0 и +1 определяются параметрами контура. Зависимость тока в контуре от величины потока совершенно подобна в этом случае зависимости возвращающей силы от угла отклонения математического маятника 7 # 6 #3, поэтому период колебаний увеличивается с ростом амплитуды.
3.3. Автоколебания
Существуют системы, в которых стационарный колебательный процесс возникает несмотря на то, что нет периодической внешней силы, заставляющей систему колебаться (с частотой, навязанной внешней силой — вынужденные колебания) и нет периодического изменения параметров системы (параметрические колебания). В такой системе имеется постоянный, не меняющийся во времени источник энергии (например, постоянная ЭДС в электрической системе, либо постоянное поле тяжести, в котором находится маятник), однако в самой системе имеется механизм, обеспечивающий периодический характер поступле-
ния энергии от источника к элементу, совершающему колебания. Колебания в таких системах называются автоколебаниями.
Важнейшим признаком автоколебаний является независимость установившегося стационарного режима колебаний (амплитуды) от начальных условий. Это отличает автоколебания от свободных незатухающих колебаний осциллятора.
Типичным примером автоколебательной системы являются маятниковые часы с гирей — так называемые «ходики». В этом случае убыль энергии (затухание колебаний маятника из-за трения) компенсируется за счет потенциальной энергии гири в поле тяжести, причем поступление энергии происходит толчками — отдельными порциями - — один раз за каждый период колебаний. Порция энергии - определяется опусканием гири на одно звено цепи, на которой эта гиря подвешена. Механизм, позволяющий гире опускаться в определенные моменты времени,
3.3 ] |
Автоколебания |
465 |
согласован с колебаниями маятника системой шестеренок и так называемым анкерным механизмом. Оказывается, что именно величина - определяет амплитуду установившихся колебаний вне зависимости от начального отклонения. Пусть, например, передача энергии маятнику (толчок, возникающий при опускании гири на одно звено) происходит в момент наибольших отклонений от положения равновесия. Если непосредственно перед очередным, -м толчком, энергия маятника (в данном случае потенциальная энергия отклоненного от положения равновесия
маятника) равна - , то после толчка его энергия - есть
- - -
Совершив одно полное колебание, маятник потеряет часть энергии из-за трения. Полагая, что сила трения пропорциональна скорости (вязкое трение), получим, что перед очередным, ( 1)-м толчком, энергия маятника станет равной
|
|
|
|
2Æ1 , |
|
|
(3.13) |
|||||||
|
- 1 - |
D |
|
|
|
|
|
|
||||||
а после |
( 1)-го толчка |
получим - |
|
|
, |
или |
||||||||
с учетом (3.13): |
|
|
|
|
|
|
|
1 - 1 - |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2Æ1 - |
|
|
(3.14) |
|||||
|
- 1 - D |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
Стационарный режим соответствует условию - |
|
|
||||||||||||
-, откуда находим |
|
|
|
|
|
|
|
|
1 - |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
- |
* |
|
|
|
(3.15) |
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
1 < |
2Æ |
|
|
|
||||||||
При |
малом затухании |
Æ, таком, |
что 2Æ 1, |
получим |
||||||||||
D 2Æ1 1 2Æ и тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- * |
1 |
|
C - |
или |
C |
2 * |
|
(3.16) |
|||||
|
|
|
|
|
|
|||||||||
|
2Æ |
2 |
|
|
|
|
|
|
* |
|
|
|
||
(C — добротность).
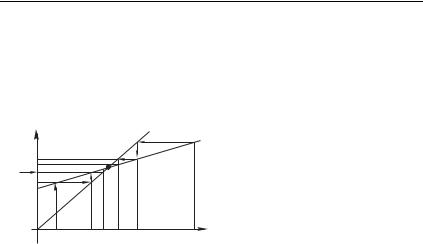
Отметим, что полученное значение энергии установившихся колебаний - не зависит от начальной энергии и начального отклонения от положения равновесия. Чтобы наглядно показать, как происходит «забывание» начальных условий, сделаем следующее построение. Выберем прямоугольную систему координат, откладывая по оси абсцисс (ось ) величину - , а по оси ординат (ось ) величину - 1 (рис. 3.5).
В этой системе координат уравнение (3.14) есть уравнение прямой
D 2Æ1 - |
(3.17) |
466 Параметрические колебания. Ангармонический осциллятор |
[ Гл. 3 |
|||||||||||||
|
Кроме этой прямой, проведем на графике биссектрису, урав- |
|||||||||||||
нение которой |
|
|
|
|
|
|
|
|
(3.18) |
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
Очевидно, точка пересечения этих прямых определяет ста- |
|||||||||||||
ционарный режим автоколебаний - 1 D 2Æ1 , что |
||||||||||||||
ясно из сравнения последнего равенства с (3.15). |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
Пусть |
начальная |
энер- |
||
|
y |
|
|
|
|
= |
x |
|
|
гия маятника, соответствую- |
||||
|
E |
|
|
|
y |
|
|
|
щая начальному отклонению, |
|||||
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
есть -1 (отмечено на оси |
|
, |
||
|
E |
|
|
|
|
|
|
|
|
|||||
E3 |
3 |
|
|
|
|
|
|
|
|
|
||||
E2 |
|
|
C |
|
|
|
|
рис. 3.5). |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
пол- |
||||
|
|
|
|
|
|
|
|
|
|
Маятник совершает |
||||
|
|
|
|
|
|
|
|
|
|
ное колебание и после перво- |
||||
|
|
|
|
|
|
|
|
|
x |
го толчка его энергия -2 най- |
||||
|
E |
E |
2 |
E |
E |
E |
E |
дется с помощью (3.14) |
|
|
|
|||
|
1 |
|
3 |
|
3 |
2 |
1 |
|
|
|
|
|
||
|
|
Рис. 3.5 |
|
|
|
|
2Æ1 - |
|
|
|||||
|
|
|
|
|
-2 -1D |
|
|
|
||||||
Значение -2 найдем с помощью прямой (3.17) на графике. Для нахождения графически следующей точки последовательно-
сти -3,
-3 -2D 2Æ1 -,
превратим «ординату» -2 в абсциссу -2 с помощью биссектрисы. Этой новой абсциссе -2 соответствует ордината-3, которая находится с помощью прямой (3.17).
Повторяя далее многократно всю процедуру, получаем ломаную кривую, заключенную между прямыми (3.17) и (3.18), которая неограниченно приближается к точке % их пересечения — стационарному режиму.
Очевидно, какую бы начальную точку мы ни взяли (например, -1 на графике) мы неизменно получаем ломаную, приближающуюся к одной и той же точке % — стационарному режиму, что и означает забывание начальных условий в процессе установления автоколебаний.
Построенная нами в соответствии с описанной процедурой ломаная кривая называется лестницей Ламерея.
3.4. Автогенератор Ван-дер-Поля
Рассмотрим теперь возникновение автоколебаний в генерато-
ре, построенном на основе электронной лампы — триода. Такой генератор называется автогенератором Ван-дер-Поля. Его схе-
ма показана на рис. 3.6.
Собственно колебательным элементом генератора является колебательный контур +, %, , находящийся в сеточной цепи

3.4 ] Автогенератор Ван-дер-Поля 467
триода. Напряжение , / % на конденсаторе контура, подается на сетку лампы. Изменение этого напряжения управляет изменениями анодного тока : (в анодной цепи лампы) и следователь-
но, изменением магнитного потока в катушке + , находящейся |
||||||||||||||||||||
в анодной цепи. Катушки + и + (катушка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
колебательного контура) индуктивно связаны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
между собой (т. е. магнитный поток катуш- |
La |
|
|
|
|
|
Ia |
|
|
|
|
|
|
|
|
|
|
+ |
||
ки + пронизывает катушку + и его измене- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния создают в последней ЭДС взаимоиндук- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
||
ции +12 , где +12 — взаимная |
L |
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
индуктивность катушек + и + . |
|
|
|
|
|
|
R |
C |
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
С помощью этого осуществляется меха- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
низм обратной связи, т. е. обратное влияние |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
анодного тока лампы на процесс колебаний |
|
|
Рис. 3.6 |
|||||||||||||||||
контура. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим качественно процесс раскачки малых колебаний, которые всегда имеют место в контуре из-за теплового хаотического движения зарядов. Пусть в данный момент времени ток : в контуре направлен так, как показано на рис. 3.6 (положитель-
ное направление обхода по контуру) |
— при этом растет заряд / |
на пластинах конденсатора, : |
& 0; растет, следователь- |
но, напряжение на конденсаторе , .
Подробнее характеристики лампы мы обсудим позднее, а пока отметим лишь, что при малых напряжениях на сетке ,c рост напряжения ,c приводит к росту анодного тока : . Последнее приводит к росту магнитного потока , созданного катушкой
+ : + : . На рисунке показано направление анодного тока, а также направление, в котором этот ток обтекает витки катушки + . Соответствующий магнитный поток направлен вверх (по правилу буравчика). Собственный же магнитный поток катушки + (по тому же правилу) направлен вниз. Нарастающий поток , пронизывая витки катушки + контура, создает
в ней ЭДС.
Каково ее направление, т. е. в каком направлении возникшая ЭДС индукции вызывает движение зарядов в контуре?
Согласно правилу Ленца возникающий индукционный ток должен создать собственный магнитный поток, направление которого должно быть таким, чтобы скомпенсировать изменение потока (который направлен вверх и нарастает). Ясно поэтому, что собственный магнитный поток тока : в контуре (направленный вниз!) также должен нарастать, а это значит, что ток : в контуре должен увеличиться.
Заметим попутно, что ЭДС взаимной индукдии +12 оказывается при этом положительной величиной: увеличивая ток :, она гонит заряды в положительном направлении обхода контура, откуда следует (поскольку & 0), что +12 ' 0.

468 Параметрические колебания. Ангармонический осциллятор [ Гл. 3
Итак, обратная связь (влияние анодного тока на колебательный контур) приводит к росту тока в контуре, к дополнительному росту заряда конденсатора и напряжению ,c, на сетке лампы. Это в свою очередь приведет к росту анодного тока и т. д.
Таким образом, имеющиеся в контуре малые колебания начинают раскачиваться, их амплитуда постепенно растет. Если
|
изменить намотку катушки + на противополож- |
||
|
ную (как показано на катушке, изображенной на |
||
|
рис. 3.7), то рост приводит к появлению ЭДС |
||
Рис. 3.7 |
в |
катушке +, |
которая приводит не к росту, а |
к |
уменьшению |
тока в контуре и, следовательно, |
|
к быстрому подавлению колебаний. Обратная связь, осуществляемая катушкой + , в первом случае называется положительной (при этом +12 ' 0), а во втором — отрицательной (+12 & 0). Итак, при положительной обратной связи возникшие в контуре малые колебания начинают нарастать, т. е. состояние покоя, при котором ток в контуре и заряд конденсатора равны нулю, неустойчиво. В случае отрицательной обратной связи, наоборот, малые колебания подавляются, т. е. состояние покоя устойчиво.
Рассмотрим теперь более детально процесс раскачки автоколебаний. Уравнение, описывающее процесс колебаний в контуре,
имеет в нашем случае вид |
|
|
|
|
|
|
: , + |
+ |
+12 |
+" |
, |
(3.19) |
|
|
||||||
|
|
|||||
|
|
|
|
по сравнению с уравнением, описывающим процесс свободных колебаний, в правой части к ЭДС индукции + добавляется ЭДС +12 . Подчеркнем, что взаимная индуктивность +12 может быть как положительной, так и отрицательной.
При положительной обратной связи +12'0. |
(имея в |
виду, что |
|||||||
|
Перепишем уравнение |
(3.19) в |
виде |
||||||
|
% 2, |
|
2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
2Æ, |
|
2 |
12 |
+" , |
(3.20) |
|
|
|
|
|
|
|||||
|
|
|
0, |
|
|
||||
|
|
|
|
|
|
; |
|
||
где Æ 2+ , а 0 1 +% .
По внешней форме последнее уравнение похоже на уравнение вынужденных колебаний (2.78), в котором правая часть играет роль внешней, вынуждающей силы. Однако принципиальное отличие нашей задачи состоит в том, что эта правая часть зависит
всвою очередь от изменений искомой функции , , (тогда как
вуравнении вынужденных колебаний правая часть — это заданная функция времени, никак не связанная (и не зависящая) от колебаний напряжения на конденсаторе контура.
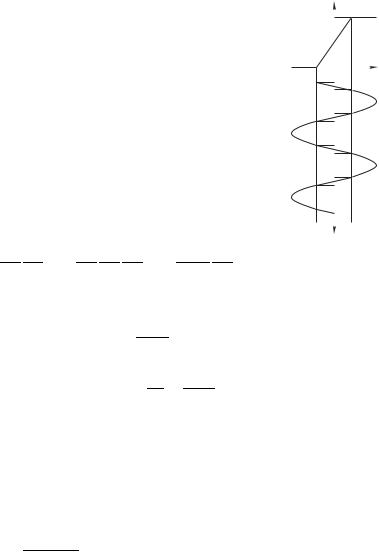
Рассмотрим идеализированную зависимость анодного тока лампы : от напряжения на сетке ,c, изображенную на рис. 3.8.
3.4 ] |
Автогенератор Ван-дер-Поля |
469 |
При |
отрицательном напряжении на сетке |
лампы, таком что |
,c ' ,1, анодный ток равен нулю — лампа заперта. При достаточно малых изменениях ,c, таких, что ,1 ,c ,2 анодный ток растет пропорционально сеточному напряжению. На этом
участке, |
как |
видно |
из графика, |
зависимость |
|
|
|
|
|
|
|
|||
: ,c имеет вид |
|
|
|
|
|
|
|
Is |
|
Ia |
||||
|
|
|
|
|
|
|
|
|||||||
|
|
: :0 90,c, |
|
(3.21) |
|
|
|
|
|
|||||
|
|
|
à |
|
I0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где 90 |
|
|
c |
— тангенс угла наклона пря- |
|
|
|
|
|
Uñ |
||||
мой на участке ,1,2 |
— константа, называемая |
|
|
|
|
|
|
|
||||||
|
|
U1 |
|
|
t1 U2 |
|||||||||
крутизной характеристики. Мы полагаем, что |
|
|
t2 |
|
||||||||||
|
|
|
|
|
|
|||||||||
на начальной стадии, в процессе раскачки, ам- |
|
|
|
|
|
|||||||||
|
|
|
t3 |
|
|
|
||||||||
плитуда колебаний настолько мала, что напря- |
|
|
|
|
t4 |
|||||||||
жение ,c не выходит за границы, где справед- |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||
лива линейная зависимость (3.21). Наконец, при |
|
|
|
t6 |
|
t5 |
||||||||
,c & ,2 имеет место насыщение: анодный ток |
á |
|
|
|
||||||||||
: достигает максимального значения :- и при |
|
|
|
t7 |
|
|
||||||||
дальнейшем росте ,c, уже не меняется. |
|
|
|
|
|
|
t8 |
|||||||
Итак, на начальной стадии, пока амплитуда |
|
|
|
|
|
|
|
|||||||
колебаний достаточно мала, мы имеем для пра- |
|
|
|
|
|
|
|
|||||||
вой части уравнения (3.20) |
|
|
|
|
|
t |
|
|
||||||
|
|
|
|
|
|
|||||||||
12 +" |
12 +" c 12(0 c |
|
|
Рис. 3.8 |
||||||||||
; |
|
|
; c |
; |
|
|
|
|
|
|
|
|
||
Перенося последнее выражение в левую часть уравнения (где |
||||||||||||||
уже есть слагаемое, содержащее производную |
c |
), получаем |
||||||||||||
|
2 c |
2 |
Æ 12(0 |
c 2 |
|
|
|
(3.22) |
||||||
|
|
|
2 |
2; |
|
0,c 0 |
|
|||||||
Введем обозначение |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Æ 12(0 |
, |
|
|
|
(3.23) |
||||
|
|
|
|
|
2 |
2; |
|
|
|
|
|
|
|
|
после чего уравнение (3.20) приобретает вид |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
0, |
|
|
|
(3.24) |
|||
|
|
|
|
,c 2Æ ,c 0,c |
|
|
|
|||||||
который совершенно подобен уравнению, описывающему свободные затухающие колебания гармонического осциллятора, причем роль затухания Æ играет величина Æ , определяемая формулой (3.23). Решение (3.24) хорошо известно:
|
|
,c D Æ , |
(3.25) |
где 2 |
2 |
, и — произвольные постоянные, завися- |
|
0 |
Æ |
|
|
щие от начальных условий. Еще раз напомним, что коэффициент Æ 2+ , определяющий изменение амплитуды колебаний
470 Параметрические колебания. Ангармонический осциллятор |
[ Гл. 3 |
при свободных колебаниях осциллятора, существенно положительная величина, поэтому показатель экспоненты D Æ всегда отрицателен, он-то и определяет экспоненциальное затухание колебаний.
Совершенно иная ситуация в нашем случае. Как следует из (3.23), величина Æ может быть как положительной, так и отрицательной. При Æ ' 0 показатель экспоненты в (3.25) оказывается положительным и мы получаем экспоненциальный рост амплитуды колебаний D Æ .
Необходимым условием выполнения неравенства Æ ' 0 является условие
+12 ' 0, |
(3.26) |
т. е. наличие положительной обратной связи (это мы уже выяснили при качественном обсуждении роли обратной связи). Условия (3.26), однако, недостаточно. Как видно из (3.23) для достижения отрицательности Æ необходимо также, чтобы выполнялось неравенство
' 12 (0 |
или |
' 12 (0 |
|
(3.27) |
||||
|
|
; |
|
; |
||||
|
|
|
||||||
Смысл последнего условия ясен: величина сопротивления контура определяет джоулевы потери энергии, а величина обратной связи +12 — ту подкачку энергии в контур, которую обеспечивает ЭДС взаимоиндукции. Для раскачки колебаний необходимо превышение подводимой энергии над потерями.
Наконец, при +12 & 0, как видно из (3.23), величина Æ всегда положительна, поэтому амплитуда D Æ всегда затухает.
Надо, однако, помнить, что все сказанное справедливо лишь до тех пор, пока напряжение на конденсаторе не выходит за границы малой области. Формула (3.25) неприменима на более поздних стадиях процесса, когда амплитуда становится достаточно большой.
Действительно, если выполнены условия (3.26) и (3.27) и величина Æ оказывается отрицательной, то, согласно (3.25), амплитуда колебаний должна неограниченно экспоненциально нарастать; при этом невозможно ответить на вопрос: какова установившаяся амплитуда автоколебаний? Кроме того, из формулы (3.25) следует, что при Æ 0 имеют место незатухающие колебания , амплитуда и начальная фаза которых зависят от начальных условий. Ни то, ни другое в действительности не имеет места. Причина несоответствия состоит в том, что даже при использовании идеализированной характеристики лампы : ,с , изображенной на рис. 3.8, крутизна 9 не является в действительности константой (равной тангенсу угла
