
Электротехнические комплексы и системы управления
.pdf
ЭЛЕКТРОТЕХНИЧЕСКИЕ КОМПЛЕКСЫ И СИСТЕМЫ УПРАВЛЕНИЯ
Межвузовский сборник научных трудов
ВЭТКиСУ
ГТУ - 2001
Воронеж 2001
23
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ АГРОУНИВЕРСИТЕТ
ВОРОНЕЖСКИЙ ИНСТИТУТ МВД РОССИИ
ЭЛЕКТРОТЕХНИЧЕСКИЕ КОМПЛЕКСЫ И СИСТЕМЫ УПРАВЛЕНИЯ
Межвузовский сборник научных трудов
Воронеж 2001
24

УДК 621.313
Межвузовский сборник научных трудов включает результаты научных исследований, проводимых специалистами ведущих вузов и промышленных предприятий г. Воронежа в области разработки новых математических методов моделирования и анализа сложных электротехнических комплексов, составляющих основу современных производственных систем.
Кроме того, в сборнике представлены статьи, рассматривающие вопросы создания программных и алгоритмических средств, ориентированных на использование в рамках автоматизированных и автоматических систем управления и базирующихся на информационных технологиях.
Сборник научных трудов подготовлен в электронном виде в текстовом редакторе MS Word и содержатся в файле ЭТКиСУ-01.zip.
|
|
Редакционная коллегия: |
В. Л. Бурковский |
- |
доктор технических наук, профессор - |
|
|
ответственный редактор, |
|
|
Воронежский государственный технический |
|
|
университет; |
С. Л. Подвальный |
- |
доктор технических наук, профессор, |
|
|
Воронежский государственный технический |
|
|
университет; |
А. И. Зайцев |
- |
доктор технических наук, профессор, |
|
|
Воронежский государственный технический |
|
|
университет; |
К. Е. Кононенко |
- |
доктор технических наук, профессор, |
|
|
Международный институт компьютерных |
|
|
технологий; |
В. Д. Волков |
- |
доктор технических наук, профессор, |
|
|
Воронежский государственный |
|
|
архитектурно-строительный университет; |
И. В. Пеньшин |
- |
кандидат технических наук, доцент, |
|
|
Воронежский институт МВД России; |
Т. А. Бурковская |
- |
кандидат технических наук, доцент - |
|
|
ответственный секретарь, |
|
|
Воронежский государственный технический |
|
|
университет |
Рецензенты: кафедра электротехники Воронежского государственного агроуниверситета; д-р техн. наук, проф. С. В. Бухарин, Воронежский институт МВД России
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
Коллектив авторов, 2001
Оформление. Воронежский государственный технический университет, 2001
25
Введение
Тематическая направленность сборника научных трудов отражает современный уровень состояния проблем моделирования, проектирования и управления электротехническими комплексами.
Публикуемые в сборнике материалы являются результатами научных исследований, проводимых авторами в вузах и промышленных предприятиях.
Рассмотрены актуальные вопросы исследования особенностей режимов работы электроприводов постоянного тока с циклической нагрузкой, характеристик асинхронных двигателей в частотно-каскадном электроприводе, средств эффективной молниезащиты промышленных объектов, секвенциальных алгоритмов для синтеза структур объектов систем безопасности, квазиустановившихся режимов при разрыве фазы в сети, а также создания специальных устройств систем электромеханики.
Кроме того, в сборнике достаточно внимания уделено вопросам использования в области анализа сложных систем аппарата нечеткой логики и нейронных сетей, а также современных пакетов прикладных программ.
Статьи реализуют единую научную методологию, основанную на применении информационных технологий моделирования и анализа.
Материалы сборника характеризуются высоким содержательным уровнем, имеют практическую направленность на решение важных инженерно-технических задач в различных объектных областях и будут полезны специалистам, занимающимся разработкой и внедрением информационных технологий в научные исследования, проектирование и управление сложными системами.
26
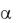
УДК 62-8.018.53.001.57
В. Д. Волков, А. В. Смольянинов ПАРАМЕТРЫ АСИНХРОННОГО ДВИГАТЕЛЯ
В ЧАСТОТНО-КАСКАДНОМ ЭЛЕКТРОПРИВОДЕ
Уточняется модель частотно-каскадного электропривода на основе учета влияния частотного управления асинхронным двигателем на параметры эквивалентной схемы цепи выпрямленного тока ротора. Предлагаются расчетные зависимости для определения параметров цепи выпрямленного тока ротора в функции частоты питающего напряжения и инженерные зависимости для расчета основных характеристик электропривода.
Современные |
требования |
к |
энергопреобразующим |
и |
регулировочным свойствам исполнительных устройств систем управления определяют целесообразность применения регулируемых электроприводов
сраздельными каналами управления и компенсации возмущений.
Вполной мере подобным свойствам разделения каналов передачи управляющих воздействий обладает частотно-каскадный электропривод /1/, целесообразность применения которого возрастает в случае построения многодвигательных систем с синхронным (общим) управлением в функции технологически значимой координаты и асинхронным (индивидуальным) регулированием частоты вращения асинхронных электродвигателей с фазным ротором (АДФ) в функции компенсируемой. В качестве компенсируемой может быть выбрана любая координата привода, в том числе и возмущение, обусловленное изменением нагрузки АДФ.
Усложнение традиционного способа каскадного управления АДФ введением частотной составляющей за счет изменения частоты питающего напряжения, расширяет регулировочные возможности электропривода (ЭП), но, вместе с тем, оказывает существенное воздействие на процессы электромеханического преобразования энергии, не позволяя тем самым использовать известные /2/ зависимости для расчета скоростных и механических характеристик ЭП. Это обусловлено известным /3/ изменением параметров двигателя при частотном управлении, не учитываемом распространенными расчетными зависимостями каскадного электропривода. Влияние частотного регулирования на расчетные параметры АДФ, управляемого по принципу асинхронно-вентильного каскада (АВК), может быть определено на основании схемы замещения (рис.1), учитывающей особенности эксплуатации двигателя в частотнокаскадном электроприводе /2,3/.
На рис.1 обозначено: U1 – статорное напряжение; U2 – напряжение
коммутируемое в ротор; - относительная частота; r1’, r2, – активные сопротивления статора и ротора; х1’, х2 –индуктивные сопротивления
27

рассеяния статора и ротора; xm – индуктивное сопротивление контура намагничивания; s – скольжение.
Схема замещения АДФ при частотно-каскадном управлении
Рис.1
На основании схемы замещения, ток фазы ротора АДФ может быть определен в виде
|
|
|
|
|
zm |
|
U1 |
U2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
z |
|
z |
|
s |
|
|
E |
|
e j s U |
|
|
|
|||
I |
|
|
|
1 |
m |
|
|
|
2k |
2 |
, |
(1) |
|||||||
2 |
|
z1zm |
|
zm |
(z1 z2 ) |
|
|
|
|
Zэ |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
z1 |
zm |
|
|
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
z1 |
|
r1 |
j |
|
x1 ; |
|
|
z2 |
r2 |
|
j x2 |
; |
zm=j |
xm; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
E |
|
e j |
K |
|
|
|
|
|
|
|
(x1 |
x m )U1 |
|
|
e j - ЭДС при неподвижном роторе; |
|
|
|
|||||||||||||
2k |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 (x |
|
x |
|
)2 |
r 2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
m ; |
|
|
|
|
- |
|
угол |
между |
|
магнитным |
|
потоком |
и ЭДС |
двигателя; |
||||||||||||
|
|
2 |
|
2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
arctg |
|
|
( |
|
|
1) |
|
|
- |
фазный |
|
угол цепи |
|
намагничивания, |
Ks |
|
1 |
|
; |
|||||||||
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||
|
|
|
x1 |
- коэффициент рассеяния статора; d |
|
r1 |
. |
|
|
|
|
|
|
||||||||||||||||||
|
|
x m |
|
x m |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из теории АВК /2,5/ известно, что используемая в расчетах основных характеристик привода эквивалентная схема замещения цепи выпрямленного тока ротора (ЦВТР) определяется приведенными к ней значениями активного и реактивного сопротивлений, образующих эквивалентное сопротивление Zэ фазы двигателя. Выделяя в Zэ необходимые составляющие, после преобразований получим
|
|
K |
|
x m x1 |
ctg2 |
( |
|
) 1 |
|
|
|
|
|
s |
x1 |
m |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Xэ x 2 |
x1 |
|
|
|
|
|
|
|
x |
2 X1Э |
(2) |
|
|
|
ctg2 ( |
m |
) |
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
K2 |
|
|
r |
|
|
|
R э |
2 |
r1 |
|
s |
|
|
2 |
R1Э , |
(3) |
s |
ctg2 ( |
m |
) 1 |
s |
|||||
|
|
|
|
|
|
|
|
|
|
28
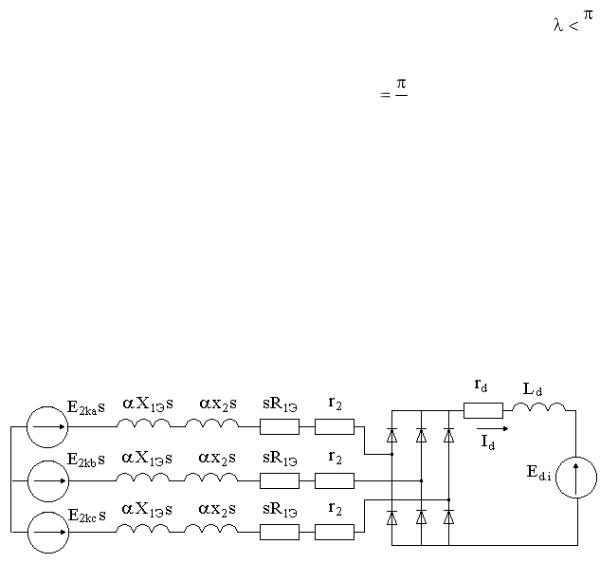
Кроме того, характерной особенностью каскадного ЭП является наличие коммутационных интервалов (интервалов перекрытия токов фаз), влияющих на энергопреобразующие свойства привода и разграничивающие возможные режимы работы роторного выпрямителя на
ряд областей. В первой рабочей области (угол коммутации |
|
) |
3 |
коммутационные потери определяются преимущественно индуктивностью фазы двигателя. Во второй рабочей области ( 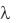 3 =const) определяющими
3 =const) определяющими
становятся коммутационные потери, связанные с запаздыванием включения вентилей роторного выпрямителя /5/.
Ток перехода во вторую рабочую область определяется известным соотношением /2/ и значительно превосходит номинальный ток, а следовательно, и момент двигателя. С учетом этого, при построении систем управления скольжением частотно-каскадного ЭП достаточно располагать эквивалентной схемой ЦВТР для первой рабочей области. Для ее определения может быть составлена эквивалентная схема цепи постоянно-переменного тока, приведенная на рис.2, где обозначено Ld, rd – индуктивность и активное сопротивление сглаживающего дросселя; Edi – постоянное напряжение вводимое в ЦВТР; Id – выпрямленный ток ротора.
Эквивалентная схема цепи переменно-постоянного тока ротора
Рис.2 Анализ эквивалентной схемы цепи переменно-постоянного тока
ротора позволяет формально получить ряд достаточно важных характеристик частотно-каскадного ЭП.
Считая ток идеально сглаженным /2/ и учитывая, что на межкоммутационном интервале ток обтекает две фазы двигателя, можно записать /4/
29
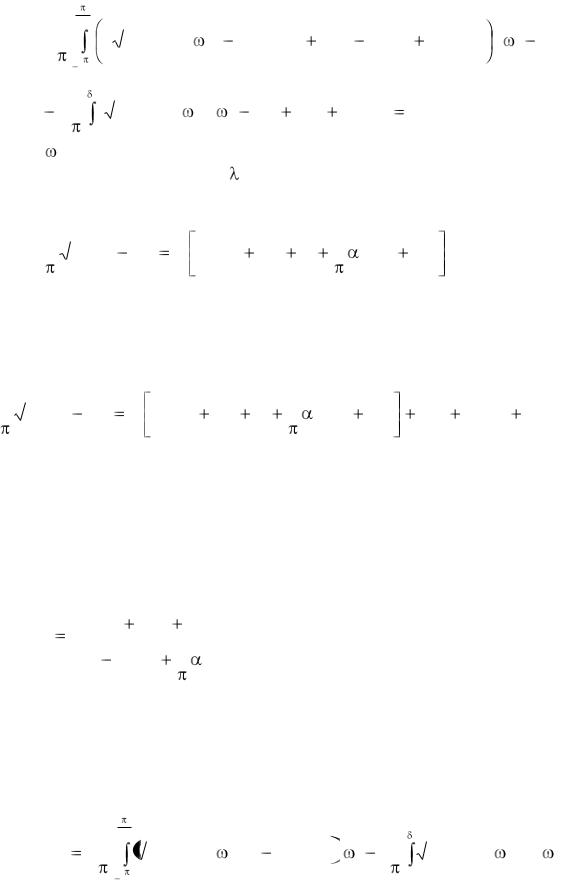
|
|
m |
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dId |
|
|
|
|
||||||
|
|
2 |
|
|
|
|
s |
|
6E |
|
|
cos( |
t) |
I |
|
(2R |
|
s |
|
2r ) |
|
2(L |
|
L |
|
) |
|
d |
t |
|
|||||||||||
|
|
|
|
|
|
|
|
|
2k |
d |
1Э |
|
|
1Э |
2 |
|
|
||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
dt |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(5) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dId |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
s |
6E |
|
|
sin( |
t)d |
t |
|
E |
|
|
I |
r |
|
L |
|
0 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
0 |
|
|
|
|
|
2k |
|
|
|
|
|
|
di |
|
|
d d |
|
|
|
d |
dt |
|
|
|
|
|
|
|
|
|
|||
где |
|
|
-круговая |
|
|
|
частота |
|
ротора; |
t-время; |
|
m2-число |
|
пульсаций |
|||||||||||||||||||||||||||
выпрямленного напряжения; |
|
- угол коммутации. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
Для трехфазного мостового выпрямителя m2 =6, что позволяет |
||||||||||||||||||||||||||||||||||||||||
записать (5) в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
||
|
|
|
|
6E2k s |
|
|
Edi |
|
Id |
2R1Эs |
|
2r2 |
|
rd |
(X1Э |
x 2 ) |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Уравнение (6) соответствует установившемуся режиму, однако как следует из (5), в переходных режимах (Id 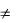 const) на электромагнитное равновесие существенное влияние оказывают индуктивности фаз двигателя и дросселя. Таким образом, учет в (4) влияния индуктивностей позволят получить уравнение динамического равновесия
const) на электромагнитное равновесие существенное влияние оказывают индуктивности фаз двигателя и дросселя. Таким образом, учет в (4) влияния индуктивностей позволят получить уравнение динамического равновесия
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
)} |
dId |
, |
|
|
6E |
2k |
s E |
di |
I |
d |
2R |
1Э |
s |
2r |
r |
(X |
1Э |
x |
2 |
) {L |
d |
2(L |
L |
2 |
|||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
d |
|
|
|
|
1Э |
|
|
dt |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Анализ (6) показывает, что вносимое электродвигателем в ЦВТР сопротивление равно удвоенной сумме активных сопротивлений статора и ротора только при условии xm>>x1>r1, что справедливо для электродвигателей большой мощности при номинальной частоте статорного напряжения, а так же позволяет установить одну из важнейших характеристик частотно каскадного ЭП, зависимость скольжения от выпрямленного тока ротора, учитывающую частотный характер управления АДФ, в виде
s |
Edи (2r2 |
|
rd )Id |
(7) |
|
Ed0 (2R1э |
3 |
Xэ )Id |
|||
|
|
||||
|
|
|
|||
|
|
|
Для определения другой, важной для исследования каскадных схем ЭП, взаимосвязи – моментно-токовой характеристики, рассчитаем среднее значение электромагнитной мощности Рэм на выходе выпрямителя. Учет коммутационных потерь и потерь в меди, которые согласно эквивалентной схеме цепи постоянно-переменного тока характеризуются активным сопротивлением RЭ1 получим
|
m2 |
m2 |
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|||
P |
|
|
|
6E |
2k |
cos( |
t)I |
d |
I2 |
2R |
1Э |
d t |
|
6E |
2k |
sin( |
t)I |
d t |
(8) |
|||||
|
|
|||||||||||||||||||||||
эм |
2 |
|
|
|
|
|
|
|
d |
|
|
2 |
|
|
|
|
d |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
30
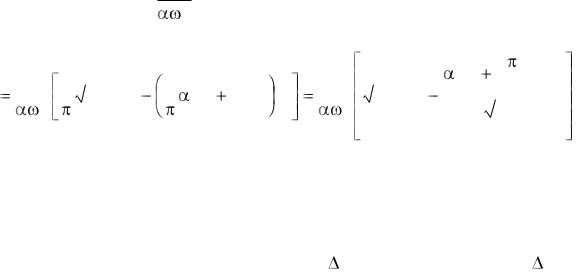
Поскольку M 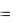 Pэм , из (8) следует выражение моментно-токовой
Pэм , из (8) следует выражение моментно-токовой
0
характеристики АДФ для первой рабочей области
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
2 |
R1э |
||
|
1 |
3 |
|
|
|
3 |
|
|
1.35 |
|
|
э |
3 |
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 |
||||||||||
M |
|
|
|
|
|
6E2k Id |
|
Xэ |
2R1э Id |
|
|
3E2k Id |
|
|
|
|
|
|
Id . |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
0 |
|
|
|
|
0 |
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Полученные зависимости позволяют определить параметры эквивалентной схемы ЦВТР и основные характеристики частотнокаскадного электропривода. В тоже время, они, при функциональном подобии, более сложны и громоздки, что требует установить степень их отличия от известных /2/. Последнее проведено на основе анализа ошибки определения эквивалентных активного r(%) и реактивного x(%) сопротивлений фазы статора, вносимых в цепь ротора (рис.3).
Ошибка определения активного и реактивного сопротивлений
31
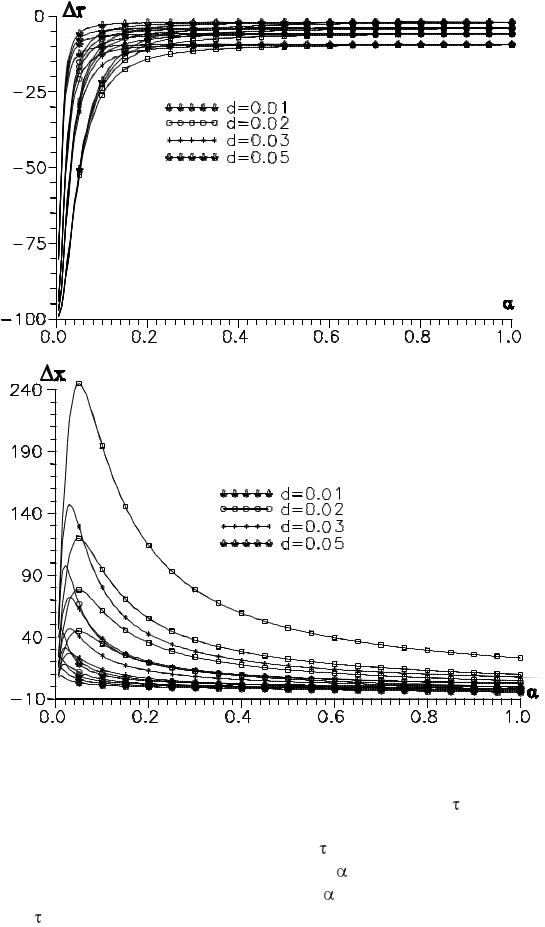
Рис.3
Расчет ошибки, проведен при ряде значений 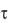 и d в функции частоты статорного напряжения, при этом большая величина ошибки при одинаковых значениях d соответствует большему значению .
и d в функции частоты статорного напряжения, при этом большая величина ошибки при одинаковых значениях d соответствует большему значению .
Анализ полученных зависимостей показывает, что ошибка
определения активного сопротивления при |
< 0,05 и номинальной частоте |
составляет менее 10% в диапазоне частот |
=0,2-1. Однако при d>0,05 |
диапазон 10% -ой точности сокращается до |
=0,5-1, откуда следует вывод, |
что при =d>0,05 необходимо использовать уточненные зависимости.
32
