
2864
.pdf
Рис.6.3 Схема к расчету гидравлического удара
Итак, слева от сечения n—n жидкость находится под прежним нормальным давлением p и движется вправо со
скоростью V1.
Справа же от сечения n—n жидкость неподвижна и испытывает давление  p .
p .
Фронт сжатия от сечения n—n быстро перемещается в сторону резервуара.
Скорость перемещения этого фронта называется скоростью распространения ударной волны.
Описанный процесс послойного сжатия будет продолжаться до тех пор, пока ударная волна не дойдет до стенок резервуара А.
Этим заканчивается первая фаза гидравлического удара.
В конце этой фазы вся жидкость в трубе неподвижна, сжата и находится под давлением  p . Часть жидкости из
p . Часть жидкости из
резервуара А вошла в трубу.
Вторая фаза. Начало второй фазы характеризуется концом первой. Жидкость в трубе С, подобно воздуху в велосипедном насосе, сжата. Если отпустить поршень в насосе при перекрытом отверстии, то воздух, расширяясь, заставит перемещаться поршень вверх; в самом цилиндре при этом начнется движение газа вверх, в сторону поршня.
Точно так же и жидкость в трубе, расширяясь, заставит
81

свои частицы двигаться в сторону резервуара.
Сначала придут в движение слои жидкости поблизости от резервуара, а затем и более отдаленные; иными словами, фронт n—n спада давления до нормального станет теперь перемещаться от резервуара к задвижке.
К концу второй фазы вся жидкость в трубе будет двигаться со скоростью V в сторону резервуара, а давление в трубе восстановится до нормального.
Третья фаза. Начало третьей фазы характерно тем, что жидкость в трубе движется в сторону резервуара со скоростью V и по инерции старается оторваться от задвижки 3.
У задвижки возникает слой жидкости, в котором давление на величину p меньше нормального.
Теперь фронт n—n пониженного давления перемещается в сторону резервуара: слева от него давление нормальное, скорость направлена влево, справа жидкость неподвижна, давление в ней на p меньше нормального. Третья фаза
закончится приходом фронта n—n к резервуару.
Четвертая фаза. Начало четвертой фазы характеризуется тем, что давление у входа в трубу со стороны резервуара нормально, т.е. равно , а со стороны трубы — меньше
нормального на p , т. е. равно p  p .
p .
Неуравновешенное состояние приведѐт к тому, что жидкость из резервуара начнет втекать в трубу со скоростью V, повышая давление в последней до нормального.
Итак, фронт нормального давления n—n теперь перемещается в сторону задвижки. Как и прежде, скорость перемещения слоя n—n равна скорости распространения ударной волны.
К концу четвертой фазы скорость во всей трубе равна V, и давление нормальное.
Так как задвижка закрыта, то, начиная с конца четвертой фазы процесс гидравлического удара, начнет повторяться.
Часть энергии жидкости при гидравлическом ударе переходит в тепло, поэтому размах колебаний давления p с
82

течением времени затухает и процесс прекращается.
Найдем расчетные зависимости для определения величины p .
Рассмотрим объем жидкости от задвижки до слоя n—n длиной s и площадью поперечного сечения .
Остановившаяся масса жидкости в этом объеме потеряла
некоторое количество движения |
за время |
t , |
в течение |
которого слой передвинулся от задвижки влево на |
s : |
||
m v |
s v . |
|
|
Импульс силы за тот же промежуток времени равен 
 t . Приравнивая импульс силы количеству движения,
t . Приравнивая импульс силы количеству движения,
получим:

 t
t 
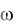 s v ;
s v ;
|
|
p |
s v |
. |
|
|
|
|
|||
|
|
|
t |
||
Обозначим величину |
s |
– скорость распространения упругих |
|||
t |
|||||
|
|
|
|
||
колебаний – через С, тогда
p  C v .
C v .
Эта формула впервые была получена Н.Е.Жуковским в
1899 году.
Н.Е.Жуковский показал, что скорость распространения ударной волны С для абсолютно жестких стенок, равна скорости распространения звука в воде.
Для скорости распространения ударной волны в случае упругих стенок им была получена формула:
C |
|
E |
Ж |
|
|
|
, |
||
|
|
d |
|
E |
|
||||
|
1 |
|
Ж |
|
|||||
|
|
|
|
|
EТР |
||||
|
|
|
|
|
|
||||
83

где С— скорость распространения ударной волны;
— плотность жидкости;
d — внутренний диаметр трубы;
— толщина стенок трубы;
EЖ и EТР — модули упругости жидкости и стенок материала трубы.
7. ЦИЛИНДР И ПРОФИЛЬ В ПОТОКЕ ИДЕАЛЬНОЙ ЖИДКОСТИ
7.1. Бесциркуляционное обтекание кругового цилиндра
Рассмотрим сложное плоское течение жидкости, получающееся в результате наложения друг на друга двух изученных ранее потоков, а именно, равномерного
прямолинейного потока, |
движущегося в направлении оси x со |
|||||||||||||||||||||||
скоростью V0 , так что |
|
V0 x и |
|
|
|
|
V0 y |
и потока, |
||||||||||||||||
получаемого от диполя, для которого |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
M |
|
x |
; |
|
|
|
|
|
|
M |
|
y |
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
r 2 |
|
|
|
2 |
|
r 2 |
|
|
||||||||||||
Потенциал и функция тока сложного течения будут |
||||||||||||||||||||||||
равны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
X |
|
|
|
|
|
|
|
|
M Y |
|
|
||||||||||
V0 X |
|
|
|
|
|
|
|
; |
|
|
|
V0Y |
|
|
|
|
|
|
. |
|||||
|
2 x2 |
|
|
y2 |
|
|
|
|
|
2 x2 |
y2 |
|||||||||||||
Чтобы найти линии тока, приравниваем функцию тока к |
||||||||||||||||||||||||
произвольной постоянной величине |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
V0 y 1 |
|
|
M |
1 |
|
|
|
|
C. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 V |
|
x2 y2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При C 0 получим уравнение для нулевой линии тока |
||||||||||||||||||||||||
|
|
|
|
V0 y 1 |
|
M |
0. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 V0 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
84

откуда следует, что y 0 и |
1 |
|
|
M |
|
|
|
|
1 |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 V |
|
x2 |
|
y2 |
|||||||
|
|
|
|
|
|
|||||||
|
|
0 |
|
|
|
|
|
|
|
|
||
Из второго условия имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
y2 r |
2 |
, |
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r0 |
|
|
|
M |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 V0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Это уравнение окружности с центром в начале координат и радиусом r0 .
Итак, нулевая линия представляет собой совокупность прямой, совпадающей с осью х, и окружности радиусом r0 с центром в начале координат (рис 7.1).
Рис. 7.1
Поток разделяется линией тока на две области – внешнюю и внутреннюю, разделенные непроницаемой для жидкости цилиндрической поверхностью.
Поверхность непроницаема для жидкости, поскольку ее поперечное сечение есть линия тока, а скорость течения по определению всегда касательная к линии тока.
Это свойство позволяет рассматривать течение во внешней и внутренней областях раздельно.
85

В частности, течение во внешней области не изменится, если заменить внутреннюю область твердым телом, имеющим форму кругового цилиндра.
Таким образом, при наложении поступательного потока на диполь получается обтекание кругового цилиндра.
При известных значениях радиуса r0 и скорости невозмущенного потока V0 момент диполя находится из равенства:
M 2 V0 r0 2 .
Подставляя момент диполя в формулы для потенциала и функции тока и учитывая, что 
 и y r sin , получаем:
и y r sin , получаем:
V0 |
1 |
r 2 |
|
r cos |
и |
|
V0 |
1 |
r 2 |
r sin . |
|||||||||||
0 |
|
|
|
|
0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
r 2 |
|
|
|
|
|
|
|
|
|
|
r 2 |
|
|
|
|||||
Проекции составляющих скорости в полярных |
|||||||||||||||||||||
координатах равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Vr |
|
|
|
d |
|
и VS |
d |
1 d |
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
dS |
r d |
|
|
|
|
|
|||||||
|
|
|
|
|
|
dr |
|
|
|
|
|
|
|
||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vr V0 |
1 |
|
r 2 |
|
|
cos |
; VS |
|
V0 1 |
|
r |
2 |
sin . |
||||||||
0 |
|
|
|
|
|
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|
r 2 |
|
|||||
На поверхности цилиндра, т.е. при r |
|
|
|
r0 , имеем: |
|||||||||||||||||
|
|
Vr |
|
|
0, |
VS |
2V0 sin . |
|
|
|
|
|
|
||||||||
Таким образом, скорость частицы жидкости на поверхности цилиндра направлена по касательной к окружности, т.е. обтекание цилиндра происходит безотрывно.
Точки А и В на цилиндре, для которых 
 и
и  0 , называются критическими, так как скорость в этих точках равна нулю.
0 , называются критическими, так как скорость в этих точках равна нулю.
Определим циркуляцию скорости вокруг цилиндра:
86

2 |
|
2 |
2 |
|
|
r0 |
|||
Г VS dS VS rd |
V0 r 1 |
|
sin d 0. |
|
r 2 |
||||
0 |
|
0 |
Таким образом, имеем бесциркуляционное обтекание кругового цилиндра.
Рассмотрим теперь силовое воздействие потенциального потока на круговой цилиндр бесконечной длины.
Сила давления, действующая по нормали к боковой поверхности цилиндра единичной длины на площадку dS , равна PdS .
Проекции этой силы на оси х и у можно записать в
виде:
dX  Pcos dS; dY
Pcos dS; dY  Psin dS.
Psin dS.
Интегрируя dX и dY , находим, что
2 |
|
2 |
X |
P cos r0 d ; Y |
P sin r0 d . |
0 |
|
0 |
Подставляя значение давления согласно уравнению Бернулли и значение скорости на поверхности цилиндра в предыдущие равенства, последние представим в виде:
|
|
2 |
|
|
|
|
|
|
|
|
X |
r |
C |
|
|
V 2 |
sin2 |
cos |
d |
0; |
|
|
|
|||||||||
|
0 |
0 |
2 |
0 |
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
X |
r |
C |
|
|
|
V 2 |
sin2 |
sin |
d |
0. |
|
|
|
||||||||
|
0 |
0 |
2 |
0 |
|
|
|
|
||
Таким образом, при бесциркуляционном обтекании цилиндра потенциальным потоком жидкости горизонтальная и вертикальная составляющие сил давления со стороны потока на цилиндр равны нулю.
В реальных условиях на цилиндр при обтекании его жидкостью всегда будет действовать гидродинамическая сила.
Противоречие между экспериментом и теоретическим выводом получило название парадокса Даламбера-Эйлера.
87

7.2. Циркуляционное обтекание кругового цилиндра
Рассмотрим случай циркуляционного обтекания кругового цилиндра, получаемого при сочетании бесциркуляционного обтекания цилиндра и циркуляционного течения, обусловленного плоским вихрем, совпадающим с осью цилиндра. В этом случае потенциал скорости и функция тока равны
V0 |
1 |
r |
2 |
r cos |
Г |
; |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
r 2 |
|
2 |
|
|
V0 |
1 |
r |
2 |
r sin |
Г |
ln r. |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
r 2 |
|
2 |
|
|
Проекции скоростей Vr и VS равны
|
Vr |
d |
V0 |
1 |
|
r |
2 |
cos |
; |
|
|
|
||||
|
|
0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
dr |
|
|
|
r 2 |
|
|
|
|
|
|
||
|
1 d |
|
V0 1 |
|
r 2 |
|
sin |
|
Г 1 |
|||||||
VS 2 dS |
|
|
r 2 |
|
|
2 r . |
||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Убедимся, что в рассматриваемом случае циркуляция скорости жидкости вокруг цилиндра равна циркуляции вихря
|
2 |
|
|
|
|
|
r0 |
2 |
|
|
|
|
2 |
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Г |
VS dS |
V0 |
1 |
|
|
|
|
sin |
rd |
|
|
|
rd |
|||
|
r |
2 |
|
0 2 r |
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
r |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
V0 r 1 |
|
|
|
cos |
Г |
|
Г. |
|
|||||||
|
|
0 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
r 2 |
|
|
|
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
На поверхности цилиндра, т.е. при r |
r0 , имеем: Vr 0. |
|||||||||||||||
|
V |
|
|
2V sin |
|
Г |
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
S |
|
|
|
|
0 |
|
|
|
2 r0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, наложение циркуляционного потока нарушает симметрию.
Картина имеет вид, изображенный на рис. 5.3.
88

Положение критических точек А и В найдем из условия VS 0 , откуда
sin |
|
Г |
|
1 |
. |
kp |
|
|
|||
|
|
4 V0 r0 |
|||
Очевидно, что при Г |
4 V0 r0 |
|
будут существовать два |
||
критических угла в 3 и 4 квадратах, как показано на рис. 7.2.
|
Рис. 7.2 |
|
|
|
|
При Г |
4 V r имеем: sin |
kp |
1 и |
kp |
2700 . |
|
0 |
|
|
||
Это означает, что обе критические точки совмещены в |
|||||
одной. |
|
|
|
|
|
Если |
принять, что Г |
4 V0 r0 , |
то получим, что |
||
sin kp 1, что невозможно.
Это означает, что критическая точка сходит с цилиндра.
89
7.3. Теорема Жуковского о подъемной силе крыла бесконечного размаха
Мы показали, что цилиндр, помещенный в потенциальный поток идеальной жидкости, не испытывает сопротивления и что в этом случае не возникает подъемной силы.
Этот теоретический вывод справедлив для тела произвольной формы.
Мы показали также, что симметричная картина обтекания цилиндра нарушается, если в потоке имеется циркуляция, возникновение которой связано с вязкостью жидкости, т.е. с трением.
Рассматривая поток идеальной жидкости (т.е. не учитывая трение), невозможно объяснить причины возникновения вихрей.
Н.Е.Жуковский, используя модель идеальной жидкости, предложил искать источник силового воздействия потока на тело в образовании циркуляции.
Он впервые установил вихревую природу сил, действующих со стороны потока на крыло, и получил зависимость между этими силами и циркуляцией скорости по контуру.
Жуковский заменил реальное крыло некоторым воображаемым жидким крылом, ограниченным замкнутой линией тока, предположив, что внутри этого жидкого крыла расположен вихрь (или система вихрей) с интенсивностью, равной сумме интенсивностей вихрей, образованных в тонком слое на поверхности тела при обтекании его реальной жидкостью.
Такой вихрь Жуковский назвал присоединенным вихрем.
Докажем теорему Жуковского о подъемной силе для частного случая обтекания кругового цилиндра при наличии циркуляции вокруг него.
90
