2864

Поэтому вихрь выходит за концы крыла и располагается вдоль по потоку, образуя, так называемые вихревые усы (рис.

8.1).

Таким образом, в первом приближении крыло конечного размаха можно заменить одним вихрем П – образной формы в плане. Вихрь, расположенный по размаху крыла, называется присоединенным, а сбегающие с торцов крыла вихревые усы –

свободными вихрями. Рис. 8.1 В рассмотренной простейшей вихревой схеме крыла

конечного размаха, согласно теореме Гельмгольца и Стокса циркуляция вдоль размаха крыла получается постоянной.

Следовательно, местная подъемная сила в каждом сечении крыла также должна быть постоянной. Это не подтверждается экспериментами.

Вихревую схему обтекания крыла, учитывающую переменность циркуляции вдоль его размаха, можно получить, если заменить крыло не одним П – образным вихрем, а системой П – образных вихрей (рис. 8.2.).

Рис. 8.2

101

Вдоль каждого такого вихря циркуляция будет постоянной, но при переходе от одного вихря к другому будет меняться.

В этой схеме можно положить число вихрей равным бесконечности, и тогда циркуляция вдоль крыла будет плавно изменяться от центра к торцам. При этом за крылом свободные вихри сольются и образуют так называемую вихревую пелену, состоящую из бесконечно большого числа сходящих с крыла вихревых шнуров.

Исследования вихревой пелены за крылом показали, что она неустойчива и вскоре после сбегания с крыла свертывается в два вихревых шнура.

Однако рассматривать такую модель крыла сложно с математической точки зрения, поэтому ее заменяют вихревой пеленой.

8.2. Скос потока и индуктивное сопротивление крыла конечного размаха

Рассмотрим действие вихревой пелены, сбегающей с крыла, на произвольную точку А (рис. 8.3.). С каждого элемента крыла dz будет сбегать элементарный вихрь с циркуляцией dГ.

Если положение точки А характеризуется координатой z, а положение элементарного вихря, сбегающего с участка крыла MN

= dz, – координатой z1 , то Рис. 8.3

скорость, индуцированная этим полубесконечным вихрем в точке А, очевидно, равна:

dГ dVy 4 (z1 z)

102

Скорость в точке А, индуцированная всей вихревой пеленой, будет равна:

где Г Г (z1 ) , а координата z для данной точки А есть величина, постоянная.

В результате скорость Vy также будет меняться по

размаху крыла, т.е. Vy Vy (z) .

Полученный интеграл несобственный. При вычислении он разбивается на два, и точка z1 z исключается.

Фактически это означает, что мы исключили из рассмотрения элементарный вихрь, проходящий через точку А, скорость Vy в которой требуется вычислить.

истинным углом атаки.

Таким образом, вблизи крыла происходит изменение

Значение этого угла невелико и составляет несколько градусов.

103

берется потому, что принято считать угол скоса положительным, когда индуцированная скорость направлена вниз, т.е. когда Vy отрицательно.

Учитывая малость угла , можно записать:

Угол скоса потока так же, как и Vy , меняется вдоль по размаху

крыла.

При отсутствии скоса потока вектор результирующей силы воздействия потока на крыло согласно теореме Жуковского нормален к направлению невозмущенного потока, т.е. к вектору V0 .

При наличии скоса потока вектор результирующей силы должен быть нормальным к направлению истинной скорости V. Следовательно, скос потока приводит к отклонению результирующей силы от направления, перпендикулярного

Эта дополнительная сила X i , появившаяся в результате

скоса потока, носит, название силы индуктивного сопротивления.

Найдем величину силы индуктивного сопротивления. Для этого выделим на крыле элементарный участок шириной dZ, на который действует подъемная сила dY. Очевидно, что индуктивное сопротивление этого участка равно:

104

Полная сила индуктивного сопротивления равна:

l / 2

X i Г (z) Vy dz .

l / 2

определяемый сопротивлением трения и разностью давлений в передней и задней частях крыла.

8.3. Основное уравнение крыла конечного размаха

Выведем уравнение, позволяющее определить закон изменения циркуляции по размаху крыла, т.е. функцию Г z .

При наличии вихревой пелены для элемента крыла dz можно написать два следующих равенства:

Приравнивая их, получаем уравнение связи:

Допустим, что угол атаки в данном сечении отсчитывается от так называемой аэродинамической хорды, т.е. от направления, для которого местный Сy 0 (рис. 8.5.).

105

Vy /V .

Рис 8.5

Таким образом, для крыла конечного размаха

Это уравнение носит название основного интегро-

106

8.4. Приближенный метод расчета распределения

циркуляции по размаху крыла

Имеется ряд приближенных методов расчета распределения циркуляции.

Рассмотрим метод Глауэрта-Трефца.

В основном уравнении сделаем замену переменной, положив:

Представим через новую переменную Vy . После преобразования получим:

Очевидно, что полученное равенство должно выполнятся в любом сечении крыла, т.е. при любом .

107

Это условие дает возможность определить коэффициенты An .

Для приближенного решения берется столько сечений крыла, сколько членов ряда Фурье желательно сохранить.

В результате получим конечную систему алгебраических уравнений для определения коэффициентов An . Необходимо

отметить, что этот метод эффективен только для крыльев простейших форм.

Таким образом, подъемная сила крыла конечного размаха выражается только через первый коэффициент разложения циркуляции в тригонометрический ряд.

Остальные коэффициенты, не изменяя общей величины подъемной силы, влияют лишь на характер распределения циркуляции по крылу, т.е. на распределение аэродинамической силы по размаху крыла.

Коэффициент подъемной силы крыла равен:

Обозначив

l 2

S

где – удлинение крыла, получим:

108

Cy A1

Найдем формулу для пересчета плоского крыла с одного удлинения на другое.

Для крыла в целом имеем:

отсюда для крыла определенной формы в плане a 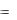A1 ,

Для данного крыла и для крыла бесконечного размаха, но с тем же значением Cy можно записать равенства

где 00 – угол атаки крыла бесконечного размаха. Из этих равенств следует:

0

00 Cy 1

Эта формула позволяет пересчитать зависимость Cy по

, известную, например, из опыта для крыла конечного размаха на крыло бесконечного размаха.

Если имеются два крыла, составленные из одних и тех же профилей, но с различными удлинениями 1 и 2 , то для них можно написать равенства:

109

2

(считается, что Cy1 Cy 2 Cy ).

Вычитая из первого уравнения второе, получаем;

Значения для различных крыльев приводятся в рекомендованной литературе.

Сила индуктивного сопротивления крыла равна:

После преобразования получим:

Коэффициент индуктивного сопротивления равен:

110