2864

Считая, что какое-нибудь событие совершается у модели в течение отрезка времени t1 , а у натурного объекта в течение времени t , найдем масштаб времени Rt .

В случае подобия эти масштабы в сходственных точках должны быть постоянными.

Все остальные масштабы других физических величин для подобных явлений также являются постоянными и могут быть выражены через эти основные масштабы.

Рис.3.1

Рассмотрим некоторые из них.

Пусть S1 и S –сходственные площади двух потоков (рис. 3.1), а l1 и l – линейные размеры этих сходственных

площадей. Очевидно, что

Понимая под сходственными отрезками времени t1 и t

такие отрезки, за которые частицы потоков проходят расстояния между двумя сходственными точками, для масштаба скоростей можно записать:

Аналогично масштаб весовой плотности потоков равен

41

Таким образом, считая, что при соблюдении подобия в пространстве, где происходят сравниваемые явления, масштабы однородных величин должны сохраняться постоянными, можно сформулировать определение подобия следующим образом:

два потока называются подобными, если в любых сходственных точках и в любые сходственные моменты времени масштабы однородных величин, характеризующих эти потоки, являются постоянными.

Такое подобие называется полным.

Если же этому условию удовлетворяют не все масштабы, а только часть из них, то подобие называется частичным.

Рассмотрим два подобных потока (рис. 3.1); один – обтекающий натурный объект, например, профиль крыла, а другой – обтекающий его модель. Выделим в жидкости два сходственных бесконечно малых элемента. Пусть на элементы будут действовать силы dR и dR1 , создающие ускорения W и

W1 . Очевидно, что

dR Wdm

dR1 W1dm1

где dm и dm1 – массы этих элементов.

Выразим массы dm и dm1 через плотность и линейные размеры:

42

dm dl3

dm1 1dl13 .

Подставляя dm и dm1 в предыдущие равенства, получаем:

Найденное соотношение справедливо, очевидно, не только для бесконечно малых объемов, но и для любых конечных объемов, так как всякий конечный объем можно разбить на бесконечно большое число бесконечно малых объемов.

Таким образом, постоянство отношений KR dR1 dR в

подобных потоках должно иметь место и для конечных объемов, на которые действует конечные силы.

Будем под R и R1 подразумевать полные

аэродинамические силы действующие на натуральный объект и модель, отношение которых при условии подобия потоков должно оставаться постоянным на любом режиме обтекания.

Переходя от масштабов к основным величинам, можно записать:

или

43

В результате выражение для силы имеет вид:

V 2 R CR 2 S

V 2 2 q – скоростной напор.

В аэродинамике наряду с аэродинамической силой рассматривается и аэродинамический момент М. Очевидно, что, проведя аналогичные выкладки, можно получить:

V 2 M Cm Sl 2

где Cm – безразмерный коэффициент аэродинамического

момента; l – характерный размер.

Полученные формулы для силы и момента являются основными формулами экспериментальной аэродинамики. С помощью этих формул по результатам эксперимента вычисляются безразмерные коэффициенты CR и Cm , которые

затем используются при проектировании самолетов.

44

3.2. Основные критерии подобия.

Понятие о ламинарном и турбулентном течениях жидкости

Итак, для двух сходственных точек модели и объекта можно записать:

где R1 R1 S1 и R RS – давления. Следовательно,

Если в потоке наряду с силами давления действуют силы трения, то, очевидно, что в динамически подобных системах силы трения должны быть пропорциональны силам давления и следовательно, касательные напряжения пропорциональны давлениям, т.е. масштаб сил давления должен быть равен масштабу сил трения.

Согласно закону Ньютона

dV

dn

Следовательно,

dV1

Для выполнения условия подобия

K P K

или

45

Re V1l1 Vl

1

Параметр Re одинаковый для двух динамически подобных течений, носит название критерия, или числа, Рейнольдса.

Величины и l входящие в число Re , представляют собой характерные для исследуемого течения скорость и длину. При подсчете числа Re для модели и объекта необходимо брать сходственные скорости и длины.

Таким образом, если в двух потоках имеет место геометрическое и кинематическое подобие и равенство чисел Re , то в этих потоках будут равны коэффициенты аэродинамических сил.

В зависимости от величины числа Рейнольдса течения подразделяются на ламинарные, или слоистые, и турбулентные, или завихренные.

Ламинарное течение характеризуется тем, что жидкость движется слоями без поперечного перемешивания.

При турбулентном течении отдельные конечные массы жидкости кроме участия в общем движении, вместе со всем потоком, совершают и свои собственные беспорядочные движения, что сопровождается интенсивным перемешиванием

46

в поперечном направлении, вихреобразованием и пульсациями местной скорости по величине и направлению.

Для сжимаемой жидкости плотность является функцией координат точек пространства и времени.

Поэтому при рассмотрении подобия сжимаемой жидкости необходимо выдерживать подобие по плотности потоков. Масштаб плотности равен

Таким образом, если у двух потоков числа M равны, то равны и коэффициенты полных аэродинамических сил, если имеет место геометрическое и кинематическое подобие, т.е. CR f M и в общем случае CR f Re, M . Следовательно,

полную аэродинамическую силу и момент можно определить по формулам:

V 2 R CR Re, M S 2

V 2 M Cm Re, M Sl 2

47

Следовательно, если при обтекании геометрически подобных тел соблюдаются числа Re и M , то коэффициенты CR и Cm будут иметь для этих тел одинаковые значения.

4.ПОГРАНИЧНЫЙ СЛОЙ

4.1.Понятие о пограничном слое

Точное решение задачи об обтекании потоком вязкой жидкости какого-либо тела, например, крыла или фюзеляжа, сводится к интегрированию сложных дифференциальных уравнений движения вязкой жидкости при заданных граничных и начальных условиях.

Внастоящее время существует ряд методов упрощения уравнений движения вязкой жидкости. Эти методы основаны на отбрасывании ряда слагаемых в уравнениях движения вязкой жидкости и дают удовлетворительное решение при малых числах Re .

Ваэродинамике самолета применяется принципиально другой метод упрощения уравнений движения вязкой жидкости, который применим при больших числах Re .

Этот метод основан на понятии пограничного слоя. Обратимся к рассмотрению физической картины

обтекания.

Допустим, что неподвижное тело, например профиль крыла, обтекается потоком воздуха (рис. 4.1).

Рис. 4.1

Экспериментально установлено, что в тонком слое вблизи поверхности тела происходит резкое нарастание скорости от нулевого значения на поверхности тела до величины порядка скорости набегающего потока.

48

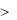
Слой воздуха, прилегающий к поверхности обтекаемого тела и представляющий собой область больших значений градиентов скорости по нормали к нему, носит название пограничного слоя.

Обычно за толщину пограничного слоя принимают расстояние от тела по нормали, на котором VX 0,9V .

Вводятся и другие определения толщины пограничного

слоя.

Частицы пограничного слоя, пройдя вдоль поверхности обтекаемого тела, уносятся потоком в область, находящуюся за телом, сохраняя следы пребывания в пограничном слое.

Это выражается, в частности, в том, что скорости этих частиц меньше скорости окружающей среды.

Заторможенные частицы образуют за телом область, называемую аэродинамическим следом. Эта область может быть заполнена и отдельными вихрями, образующимися в пограничном слое из-за наличия градиента скорости. В этом случае область за телом представляет собой так называемый вихревой след.

Внутри пограничного слоя и следа, где градиенты скорости значительны, силой внутреннего трения пренебрегать нельзя, и жидкость или газ, движущиеся внутри пограничного слоя, следует считать вязкими даже при малом значении коэффициента вязкости.

Вне пограничного слоя и следа за телом, где градиенты скорости малы, силой внутреннего трения можно пренебречь, т.е. считать жидкость идеальной, а поток безвихревым (потенциальным).

49

4.2. Интегральное соотношение для пограничного слоя

Рассмотрим течение жидкости над криволинейной поверхностью малой кривизны (рис. 4.2). В этом случае

удобно ось координат Ox считать криволинейной, расположив ее на обтекаемой поверхности вдоль течения.

Выделим в пограничном слое бесконечно малый объем, имеющий единичную ширину и ограниченный поверхностью АС верхней границы пограничного слоя и

плоскостями АВ и СD, Рис. 4.2 отстоящими друг от друга на расстоянии dx .

Применим к объему АВСD теорему о количестве движения.

Вычислим изменение количества движения в

Таким образом, через участки АВ и СD будет вытекать количеств жидкости

50