
2864
.pdf
Определим силовое воздействие потока на круговой цилиндр с радиусом r при его циркуляционном обтекании идеальной жидкостью.
Поскольку жидкость идеальная, то на поверхности цилиндра будут действовать только силы давления.
Выделим на цилиндре участок высотой, равной единице.
В окрестности произвольной точки, находящейся на
окружности цилиндра, элементарная сила давления равна |
pdS , |
||
где dS - элементарная |
длина дуги. Ее проекции на |
оси |
|
координат равны |
|
|
|
dX |
p cos |
dS |
|
dY |
p sin |
dS |
|
Используя уравнение Бернулли, после преобразования и интегрирования, предыдущие равенства представим в виде
|
2 |
|
|
|
pV 2 |
|
; |
||
X |
r0 |
C |
|
|
|
cos |
d |
||
|
2 |
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
pV |
2 |
|
|
|
Y |
r0 |
C |
|
|
|
sin |
d . |
||
|
2 |
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В результате имеем: |
|
|
|
|
|
|
|
|
|
|
|
X |
0 |
|
|
|
|
||
Это означает, |
что |
сила |
лобового |
сопротивления при |
|||||
циркуляционном обтекании кругового цилиндра бесконечной длины потоком идеальной жидкости равна нулю, т.е. и здесь имеет место парадокс Даламбера-Эйлера.
После определения проекции силы на ось y получим,что
Y pV0 Г
Эта формула называется формулой Жуковского и является основной формулой аэрогидродинамики.
Таким образом, получен весьма важный результат: при обтекании цилиндра поступательно циркуляционным потенциальным потоком невязкой жидкости со стороны потока на единичную длину цилиндра в направлении оси Y действует
91

сила, равная произведению плотности жидкости, циркуляции скорости и скорости набегающего потока.
Направление подъемной силы можно определить, повернув вектор скорости невозмущенного потока V0 на
прямой угол в сторону, противоположную направлению циркуляции.
Вданном случае в точках, лежащих на одной вертикали, давление на верхней поверхности цилиндра меньше, чем на нижней, а скорости течения, наоборот, на верхней поверхности больше, чем на нижней.
Врассмотренном выше циркуляционном обтекании цилиндра последний можно заменить одиночным вихрем той же интенсивности, что и цилиндр. Формально можно заменить любое обтекаемое тело соответствующей системой вихрей.
На возможности замены тела эквивалентной системой вихрей впервые указал Н.Е.Жуковский.
С помощью метода конформного отображения можно перейти от течения вокруг кругового цилиндра к течению вокруг профиля.
Метод конформного преобразования изложен в приведенной литературе.
7.4. Теория тонкого профиля
Крылом называют тело, которое создает в потоке жидкости подъемную силу, значительно превышающую силу
любого сопротивления. |
|
|
|
|
|
|
|
|
|
|
Отношение подъемной |
силы |
крыла Y к лобовому |
||||||||
сопротивлению Q называется качеством крыла K , т.е. |
||||||||||
|
|
|
Cy S |
|
pV 2 |
|
|
|
|
|
K |
Y |
|
2 |
|
|
Cy |
|
|||
|
|
|
|
|||||||
Q |
|
Cx S |
|
pV 2 |
|
C |
x |
|||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
Как правило, крыло самолета имеет форму, симметричную относительно некоторой плоскости – плоскости
92
симметрии. |
|
|
|
Любое сечение |
крыла плоскостью, параллельной |
||
|
|
плоскости |
|
|
симметрии |
крыла, |
|
|
|
называется |
|
|
профилем крыла. В |
||
|
разных |
сечениях |
|
|
профиль |
крыла |
|
|
может |
|
быть |
|
различным |
по |
|
|
форме, |
размерам и |
|
|
ориентации. |
Один |
|
|
из |
возможных |
|
|
|
профилей |
|
|
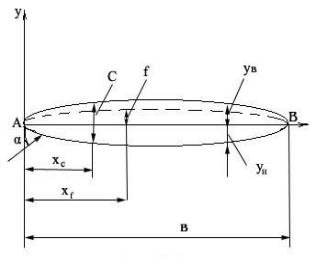
изображен на рис. |
||
|
7.3. |
|
|
Рис. 7.3 |
Точки А - передняя |
||
кромка профиля, В - задняя кромка, или точка схода профиля. Линия АВ, соединяющая две наиболее удаленные точки
профиля, т.е. переднюй и заднюю кромки профиля, называется хордой профиля.
Хорда делит профиль на две части – верхнюю и нижнюю.
Угол между хордой профиля и направлением невозмущенного потока называется углом атаки а, если вектор скорости невозмущенного потока параллелен плоскости профиля.
При изучении геометрических характеристик профиля пользуются прямоугольной системой координат, начало которой помещают на передней кромке, ось x направляют вдоль хорды по направлению к задней кромке, ось y - вверх.
В этой системе координат осей уравнения верхнего и нижнего контуров профиля соответственно имеют вид:
Yb 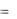 f1 ( X ) YH
f1 ( X ) YH 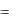 f2 ( X )
f2 ( X )
93
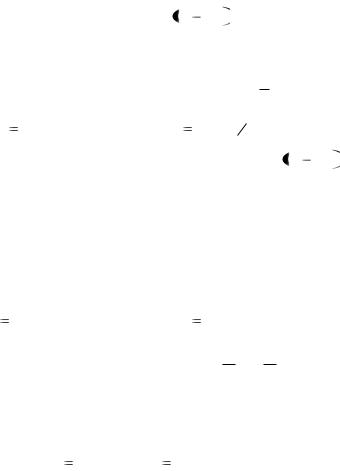
Толщина профиля в произвольной точке хорды
выражается как разность ординат |
точек Yb |
и YH . |
|
|
Наибольшая |
разность |
YB |
YH |
называется |
максимальной толщиной, или просто толщиной, профиля и обозначается C .
Отношение максимальной толщины профиля C к хорде
b носит название относительной толщины профиля C , т.е.
|
|
|
C |
|
|
|
C |
|
|
C |
|
, или в процентах, C |
100 0 0 |
||||
|
|
b |
b |
|||||
|
|
|
|
|
|
|
||
Линия, |
соединяющая середины |
отрезков YB YH , |
||||||
построенных в разных точках хорды, называется средней линией профиля.
В частном случае, когда профиль симметричен, средняя линия совпадает с хордой.
Наибольшая ордината средней линии называется кривизной профиля f , а ее отношение к хорде b называется
относительной кривизной, т.е. |
|
|
|
|
||||
|
|
|
f |
, или, в процентах, |
|
|
f |
|
|
f |
|
f % |
100% |
||||
|
|
b |
b |
|||||
|
|
|
|
|
|
|
||
Абсциссы наибольшей толщины профиля и наибольшей
кривизны соответственно обозначаются через X c и X f . Отношения этих величин к хорде b носят названия
относительных абсцисс соответственно толщины и кривизны,
т.е. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
X |
c |
|
|
|
X f |
|
|
|
|
X c |
|
X f |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
b |
|
|
b |
|||
|
|
|
|
|||||||||
Значения X c у |
дозвуковых профилей колеблются в |
|||||||||||
пределах 25-30 % , у сверхзвуковых - 40-50 % . |
||||||||||||
Относительные |
толщины |
аэродинамических профилей |
||||||||||
крыльев и лопастей винтов обычно находятся в пределах от 3-4 % до 20-25 % .
Тонкие профили применяются на концах лопастей винтов и на крыльях сверхзвуковых самолетов.
94

Относительная кривизна современных профилей крыльев и лопастей винтов обычно не превышает 2 % .
Кривизна профилей самолетов 20-30-х годов доходила до 6-8 % .
Ограничимся рассмотрением простейшей задачи теории тонкого профиля, основанной на замене профиля непрерывно распределенными по его средней линии вихрями и впервые
рассмотренной английским ученым Глауэртом. |
|
Введем понятие о погонной циркуляции |
в данной |
точке произвольной кривой, вдоль которой непрерывно распределены вихри.
Выделим на этой кривой элемент |
S и обозначим через |
|||||
Г циркуляцию скорости |
от |
вихрей, |
расположенных на |
|||
элементе S . |
|
|
|
|
|
|
Погонной циркуляцией |
в точке называется |
|||||
lim |
Г |
|
dГ |
|
|
|
S |
|
dS |
|
|||
S |
0 |
|
|
|||
|
|
|
|
|
||
Введя понятие погонной циркуляции 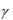 x , обратимся к
x , обратимся к
рассмотрению теории тонкого профиля.
Допустим, что плоский установившийся поток идеальной несжимаемой жидкости, движущейся на бесконечности с заданной скоростью V00 , обтекает тонкий
профиль, длина которого ОА = b.
Поместим начало координат в передней кромке профиля, ось x направим вдоль хорды к задней кромке профиля, ось y - перпендикулярно ей вверх (рис. 7.4).
|
Введем |
следующие |
|
|
упрощения: |
|
|
|
–будем |
считать |
профиль |
|
достаточно |
тонким, |
мало |
|
отличающимся от своей средней |
||
|
линии ОА; |
|
|
Рис. 7.4 |
–предполагая |
|
профиль |
95

слабоизогнутым, получаем, что его средняя линия ОА незначительно отличается от прямой ОА, являющейся хордой профиля;
–будем предполагать, что обтекание этого тонкого слабоизогнутого профиля происходит под малым углом атаки.
Заменим профиль непрерывно расположенными по его средней линии ОА вихрями, напряжение которых на элементе
dx обозначим через |
x dx . |
Функцию |
x следует подобрать из условия, чтобы |
поток обтекал профиль без срыва, т.е. его средняя линия являлась линией тока.
Учитывая, что профиль слабоизогнут, будем считать, что вихри расположены вдоль хорды профиля, а не на его средней линии. Тогда скорость, индуцируемая вихрями в точке x1 хорды, будет равна:
b |
|
(x)dx |
|
|
Vi |
|
. |
||
|
|
|||
2 |
(x x1 ) |
|||
0 |
|
Эту индуцированную скорость Vi x1 на хорде профиля
можно принять равной индуцированной скорости на поверхности профиля, имея в виду введенные раньше упрощения.
Наличие этой скорости изменит угол атаки на величину  , так что
, так что
tg |
Vi |
|
V00 |
||
|
и местный угол атаки будет равен  VVi .
VVi .
Для того, чтобы профиль обтекался безотрывно, необходимо, чтобы в каждой его точке местная скорость была направлена по касательной к поверхности профиля, т.е. должно иметь место равенство
Vi dy , V00 dx
96

где y y(x) – заданное уравнение средней линии профиля, т.е. dy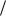 dx – известная функция. Подставляя в полученное уравнение значение Vi , получаем:
dx – известная функция. Подставляя в полученное уравнение значение Vi , получаем:
1 |
b |
(x)dx |
|
dy |
|
|
|
. |
|||
|
|
|
|
||
2 V00 |
0 |
x x1 |
|
dx |
|
Полученное равенство представляет собой интегральное уравнение относительно неизвестной функции 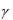 x .
x .
Решение основано на введении новой независимой переменной , определяемой равенством
|
|
x |
|
|
b |
(1- cos |
) . |
|
|
|
|||||||
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Очевидно, что при изменении х в пределах 0 < х< b |
|||||||||||||||||
меняется от 0 до . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
ищется в виде ряда Фурье |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
00 |
|
|
|
||
( |
) |
2V00 ( A0ctg |
|
|
|
|
|
Ansin n |
|
||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
n |
1 |
|
|
|
|||||
После преобразований уравнение, соответствующее |
|||||||||||||||||
условию безотрывного обтекания профиля, принимает вид |
|||||||||||||||||
|
|
|
00 |
|
|
|
|
|
|
|
|
|
dy |
|
|||
|
|
A0 |
|
|
|
An cos n |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
n 1 |
|
dx |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Коэффициенты |
An |
этого |
уравнения |
определяются |
|||||||||||||
методом, обычным для рядов Фурье. |
|
|
|
|
|||||||||||||
Умножая |
обе |
части последнего |
уравнения на |
||||||||||||||
1,cos ,cos2 ,cos3 |
,... |
и |
интегрируя |
в пределах от 0 до . |
|||||||||||||
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
1 |
|
|
|
dy |
d |
|
||||
|
|
0 |
|
|
|
|
|
|
|
0 dx |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A |
2 |
|
|
dy |
cos n |
d |
|
|||||||||
|
|
|
|
|
|
||||||||||||
|
|
n |
|
|
|
dx |
|
|
|
|
|
|
|||||
|
|
|
0 |
|
|
|
|
|
|
||||||||
97

где |
dy(x) |
выражено через |
|
с помощью подстановки |
dx |
|
|||
|
|
|
|
|
|
|
x |
b |
(1 cos ) . |
|
|
2 |
||
|
|
|
|
Найдя значения коэффициентов, определим погонную циркуляцию  X
X  и индуцированные скорости, т.е. задача об
и индуцированные скорости, т.е. задача об
обтекании тонкого профиля решена.
Теперь можно найти подъемную силу, действующую на профиль:
|
|
|
|
dY |
p (x)dxV00 . |
|
|
||||||||||||
Переходя к переменной |
и учитывая, что dx |
b |
sin d |
||||||||||||||||
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dY |
|
b |
|
|
|
sin |
d |
V00 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
00 |
|
|
|
|
|
|
|
|
|
Y pV 2 b [ A (1 cos |
) |
|
|
A sinn sin ] d |
|
|
|||||||||||||
00 |
|
0 |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
pV |
2 |
b |
( A |
|
A1 |
) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
00 |
|
|
0 |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
Y |
|
|
|
2 |
( A |
|
|
A1 |
) . |
|
|
|||
y |
|
b1 pV 2 / 2 |
|
|
|
|
|||||||||||||
|
|
|
0 |
2 |
|
|
|
||||||||||||
Аналогично вычисляется момент относительно передней |
|||||||||||||||||||
кромки профиля: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
||
|
|
|
M |
pV |
(x) x dx |
|
|
||||||||||||
0
Переходя к переменной , после вычислений получаем:
M |
|
pV 2 b2 |
( A A1 |
A2 |
) , |
|
|
||||
|
4 |
00 |
0 |
2 |
|
|
|
|
|
откуда
98
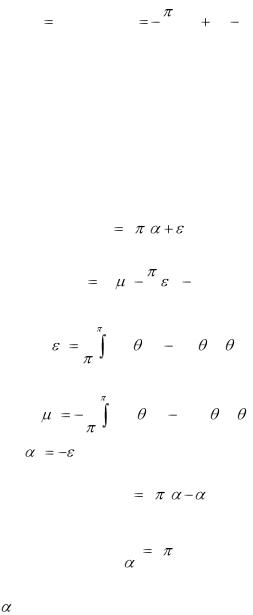
C |
M |
|
|
( A |
A |
A2 |
) |
b1b pV 2 / 2 |
|
|
|||||
m |
2 0 |
1 |
2 |
|
|||
Таким образом, значения подъемной силы и момента определяются лишь первыми тремя коэффициентами разложения погонной циркуляции в ряд.
Остальные коэффициенты ряда влияют только на распределение местных скоростей (а стало быть, и давлений) по профилю,
Подставляя значения |
A0 , A1 , A2 |
в формулы для Сy и Cm |
|||||
получаем: |
|
|
|
|
|
|
|
Cy |
2 |
( |
|
0 ) |
|
||
и |
|
|
|
|
|
|
|
Cm 2( |
|
|
|
0 ) |
|
1 |
Cy |
0 |
4 |
4 |
|||||
|
|
|
|
||||
где
0
и
|
|
0 |
Угол |
0 |
0 |
|
подъемной силы, т.е.
откуда
Следовательно,
1 |
|
|
dy |
|
( |
) (1 cos ) d |
|
|||
|
|
|
0 dx |
|
||||||
|
|
|
|
|
|
|
||||
|
1 |
|
|
dy |
( |
) (1 |
cos2 ) d |
|
||
|
|
|
0 dx |
|
||||||
|
|
|
|
|
|
|
||||
|
|
|
называется |
углом атаки |
нулевой |
|||||
|
|
|
|
|
Cy |
2 ( |
0 ) , |
|
||
|
|
|
|
|
dCy |
2 . |
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
d |
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
для |
тонких |
профилей Сy |
линейно |
||||||
зависит от , а производная не зависит от формы профиля. Выражение для коэффициента момента можно записать
в виде:
99
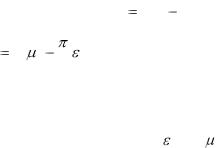
|
|
Cm |
Cm0 |
1 |
Cy , |
|
|
|
4 |
||||
|
|
|
|
|
||
где Cm0 2( 0 |
|
0 ) – коэффициент момента при нулевой |
||||
4 |
||||||
|
|
|
|
|
||
подъемной силе.
Таким образом, определение аэродинамических коэффициентов для тонкого профиля сведено к вычислению двух простых интегралов для 0 и 0 , что не представляет
труда, так как форма профиля известна.
Формулы для Сy и Cm хорошо согласуются с опытными
данными для профилей небольшой относительной кривизны и толщины.
Теория тонкого профиля находит наибольшее применение лишь в задачах, требующих определения суммарных аэродинамических характеристик профиля, так как получаемое с ее помощью распределение местных скоростей (давлений) по профилю значительно отличается от реального распределения.
8. ТЕОРИЯ КРЫЛА КОНЕЧНОГО РАЗМАХА
8.1. Модели крыла конечного размаха
Ранее было показано, что действие вихря с циркуляцией Г, находящегося в потоке, создает такую же подъемную силу, как и крыло, имеющее ту же циркуляцию.
Таким образом, воздействие крыла на жидкость можно заменить действием вихря бесконечной длины.
Если крыло имеет конечную длину, то подъемная сила крыла будет равна подъемной силе, создаваемой отрезком вихря длиной, равной длине крыла.
По теореме Гельмгольца вихрь не может обрываться в жидкости.
100
