2864

предыдущее уравнение, придем к формуле Прандтля:

VV1 aкр2

Из формулы Прандтля следует, что в прямом скачке уплотнения критическая скорость aкр является средним

геометрическим между скоростями до и после скачка уплотнения, т.е. в прямом скачке уплотнения всегда осуществляется переход от сверхзвуковой скорости к дозвуковой.

Формулу Прандтля можно представить в виде

131

получим соотношение для плотностей и давлений до, и после скачка:

p p1 , получим связь между отношениями температур и давлений до, и после скачка:

Как видно, эти зависимости сильно отличаются от зависимостей в изоэнтропическом процессе, где

132

Сравнение процессов изменения параметров газа в прямом скачке с обратимым адиабатическим процессом (изоэнтропическим) показывает, что в скачке происходит более быстрый рост температуры, объясняемый необратимым переходом части механической энергии в тепловую, вызывающим дополнительный нагрев газа.

Увеличение температуры в скачке приводит к более медленному росту плотности.

Из уравнения (*) получим, что при p p1

Кривая, построенная по уравнению (*), называется ударной адиабатой, или адиабатой Гюгонио.

Из уравнения неразрывности следует, что в этом случае скорость после скачка также уменьшается только в 6 раз (а не до нуля).

9.8. Давление в критической точке за прямым скачком

При обтекании сверхзвуковым потоком тел с тупой передней частью на некотором расстоянии впереди тела образуется отсоединенный скачок уплотнения (рис.9.6), который изменяет величину давления в критической точке. Поток до и после скачка останется изэнтропическим.

В этом случае давление торможения равно:

133

Используя соотношение между и м , предыдущее равенство представим в виде:

134

Если предположить, что имеет место изэнтропическое торможение сверхзвукового потока, то получим;

p01 I 0,2M2 3,5 p1 1

Давление в критической точке при наличии прямого скачка уплотнения оказывается меньшим, чем при изэнтропическом торможении, на величину потерь давления в прямом скачке.

Коэффициент потерь полного напора равен

9.9. Косые скачки уплотнения

Рассмотрим обтекание сверхзвуковым потоком внутреннего тупого угла АОВ (рис.9.7).

Рис. 9.7

Поток протекает параллельно стенке АО со скоростью V1 , затем отклоняется на угол 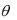и приобретает новую скорость V, направленную параллельно стенке OВ.

135

В этом случае, как мы знаем, возникает косой скачок уплотнения.

Предположим, что фронт косого скачка уплотнения образует угол с направлением невозмущенного потока.

Очевидно, что при 2 получим прямой скачок, который является частным случаем косого скачка уплотнения.

Обозначим параметры газа до скачка через p1,V1, 1,T1, а после скачка через p,V , ,T .

Разложим векторы скорости до и после скачка на нормальные и касательные к фронту скачка составляющие.

Уравнение количества движения в направлении, перпендикулярном к фронту скачка, представим в виде

p p1 ρ1 V1n V1n Vn

Так как силы давления вдоль плоскости скачка не меняются, то уравнение количества движения в направлении, параллельном плоскости скачка, можно представить так:

ρ1 V1n V1t Vt 0

Следовательно, касательные составляющие скорости до и после скачка равны между собой, т.е.

V1t Vt ,

а разрыв претерпевают только нормальные составляющие. Уравнение энергии запишем как

Уравнение неразрывности преобразуется к виду

ρ1V1n ρVn ,

так как массовый расход через плоскость скачка зависит только от нормальной составляющей скорости.

Из последнего равенства следует, что

136

Сучетом этого равенства уравнение изменения

количества движения после умножения на Vn 1 принимает вид

Из уравнения энергии следует, что

Подставляя полученные соотношения в уравнение неразрывности, придем к соотношению

Это соотношение позволит определить скорость за косым скачком.

Она может быть как дозвуковой, так и сверхзвуковой. Для косого скачка можно записать, что

V1n V1 sin β

Введем условное число

Подставив в формулы прямого скачка вместо М величину М1, получим соотношения для определения плотности давления и температуры за косым скачком

137

Уравнение ударной адиабаты остается тем же, так как в него не входит ни скорость, ни полная энергия.

меняться, то скорость V за скачком также будет меняться. Кривая, которую описывает конец вектора V, называется ударной полярой.

Очевидно, что в плоскости Vx ,Vy , , которая называется

плоскостью годографа скорости, ударную поляру можно представить как зависимость

Vy f Vx

Рис. 9.8

В плоскости годографа скорости соотношения между составляющими скоростей представлены на рис. 9.8.

Очевидно, что

Vx Vt cos β Vn sin β , Vt V1 cos β V1n V1 sin β

138

или

139

ударной поляры, является кривой 3-го порядка и называется гипоциссоидой, или строфоидой.

Для более удобного пользования полученной формулой приведем ее к безразмерному виду, разделив обе части на aкр2 и введя обозначения

Тогда

Рис. 9.9

Этой формуле соответствует кривая, приведенная на рис. 9.9. Петля этой кривой называется ударной полярой.

Радиус вектор любой точки гиподиссоиды дает величину

140