
Интегральное исчисление функции одной переменной. Дурова В.Н., Зайцева М.И
.pdf
Примеры:
1. |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
ln |
|
t |
|
|
c |
ln |
tg |
x |
|
c |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
sin x |
|
|
|
|
|
1 t2 |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
sin x |
|
|
|
2t |
, dx |
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
t2 |
|
|
|
1 t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
tg |
|
|
|
|
|
|
c; |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
cos x |
|
|
|
sin |
x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
x |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3. |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
3sin x |
|
2 cos x |
|
2 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
1 t2 3 |
2t |
|
2 |
1 t2 |
|
2 |
|
|
|
|
|
6t |
|
2 2t 2 |
|
2 2t 2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
t2 |
|
1 |
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2dt |
|
|
1 |
|
d 3t 2 |
|
1 |
|
|
|
|
1 |
|
x |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
3t 2 |
|
c |
|
ln |
3tg |
2 |
c |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
6t |
4 |
3 |
|
|
|
|
3t |
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Замена переменной (15) называется универсальной тригонометрической подстановкой, т.к. с еѐ помощью интеграл (14) всегда приводится к интегралу от дробно – рациональной функции. Однако пользоваться этой подстановкой не всегда целесообразно, так как часто она приводит к громоздким выкладкам. Поэтому в некоторых частных случаях используют другие подстановки.
41
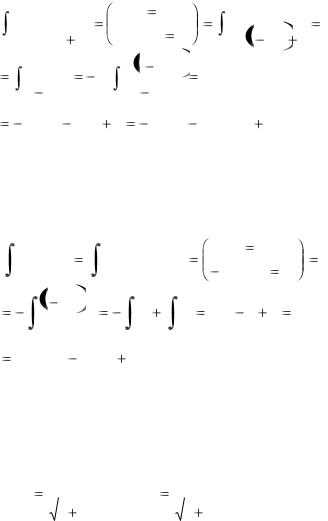
2.Частные случаи интегрирования тригонометрических выражений.
1) Если подынтегральная функция нечѐтна относительно cosx: R(-cosx, sinx) = -R(cosx,sinx), тогда замена sinx = t
рационализирует интеграл (14);
Пример:
sin x cos xdx |
|
sin x |
|
t |
|
|
|
tdt |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos2 t |
1 |
|
|
cos xdx dt |
2 1 |
t 2 1 |
||||||||||||
|
|
|
tdt |
|
|
1 |
|
d 3 |
2t 2 |
|
|
|
|
|
||||
|
3 2t 2 |
|
|
4 |
3 |
2t 2 |
|
|
|
|
||||||||
|
|
1 |
|
2t 2 |
|
|
1 |
ln |
|
3 |
2sin2 x |
|
|
|||||
|
|
ln |
3 |
|
c |
|
|
c |
||||||||||
4 |
|
4 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) Если подынтегральная функция нечетна относительно sinx: R(cosx, -sinx) = -R(cosx, sinx), тогда замена cosx = t рационализирует интеграл (14);
Пример:
|
sin3 x |
|
|
sin2 x sin xdx |
cos x |
|
|
|
t |
||||||||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
cos4 x |
|
|
|
cos4 x |
|
|
|
sin xdx dt |
|||||||||||
|
|
1 t2 dx |
|
|
dt |
|
dt |
|
1 |
|
1 |
c |
|||||||
|
|
|
t4 |
|
|
|
|
t4 |
|
t2 |
|
3t3 |
|
|
t |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
1 |
c |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3cos3 x |
cos x |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3) Если подынтегральная функция чѐтна и относительно sinx, и относительно cosx, т.е. R(-cosx, -sinx) = R(cosx, sinx),
то замена tgx = t рационализирует интеграл (14).
Воспользуемся тригонометрическими равенствами:
sin x |
|
tgx |
|
; cos x |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
1 tg 2 x |
|
tg 2 x |
|||||||
|
1 |
|
|
||||||
Найдем дифференциал dx.
42
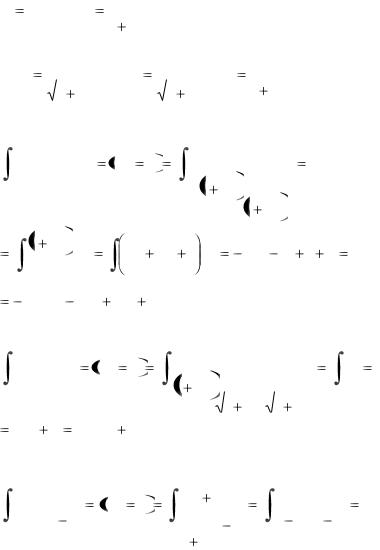
|
x arctgt; dx |
|
|
|
|
|
dt |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Окончательно получим замену: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|||||||||||||||||
sin x |
|
|
|
|
|
|
|
|
|
|
|
; cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
; dx |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
1 |
|
t 2 |
|
1 |
|
|
t 2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
tgx |
t |
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
sin4 x cos2 x |
|
|
|
|
1 |
|
|
|
t2 |
|
|
|
t |
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
t |
2 2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
t |
2 2 |
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
1 dt |
|
|
|
|
|
|
|
|
t |
c |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
t4 |
|
|
|
|
|
|
|
t4 |
|
|
t 2 |
|
|
|
|
|
3t3 |
|
|
|
|
t |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
tgx |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
3tg3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
tgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Пример 2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
tgx |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
sin x cos x |
1 |
|
t2 |
|
|
|
|
|
|
t |
|
|
1 |
|
|
|
|
|
|
|
t |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
t2 |
|
|
1 |
|
|
t2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
ln |
t |
|
|
c |
|
ln |
tgx |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 3: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
tgx |
t |
|
|
|
|
|
|
|
|
1 |
|
|
|
t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
x |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
4t |
2 |
4 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
43
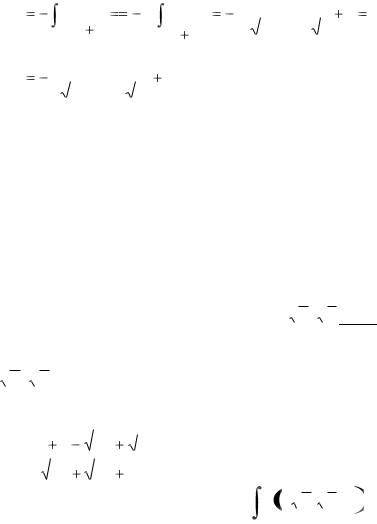
|
|
|
dt |
|
|
1 |
|
|
|
dt |
|
|
1 |
|
2 |
|
arctg |
2 |
t |
|
c |
|||||||
|
4t 2 |
|
|
|
4 |
|
3 |
|
|
4 |
|
|
|
|
|
|||||||||||||
|
3 |
|
t |
2 |
3 |
3 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
arctg |
2tgx |
|
c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.12. Интегрирование некоторых иррациональных выражений
Интегрирование не всякого иррационального выражения возможно в элементарных функциях. В некоторых простейших случаях иррациональные функции можно рационализировать с помощью замены переменной, а значит и проинтегрировать в конечном виде.
1. Интегрирование функций вида R(x, n x, m
x, m x , ,…)
x , ,…)
Здесь символ R указывает, что над величинами
x, n x , m
x , m x … выполняются только рациональные операции: сложение, вычитание, умножение, и деление. Например:
x … выполняются только рациональные операции: сложение, вычитание, умножение, и деление. Например:
|
|
|
|
|
|
|
|
x2 x |
3 x2 |
5 |
|
|
|||
x |
|
||||||
|
|
|
|
|
|
|
|
3 x5 |
|
x3 |
x |
|
|||
Пусть надо вычислить интеграл R x, m x , n
x , n x ,... dx , где
x ,... dx , где
числа m, n,… могут быть и отрицательными. Подберѐм число N так, чтобы при замене переменной x = tn все корни извлекались. (N – НОК чисел m, n,…). Тогда:
44
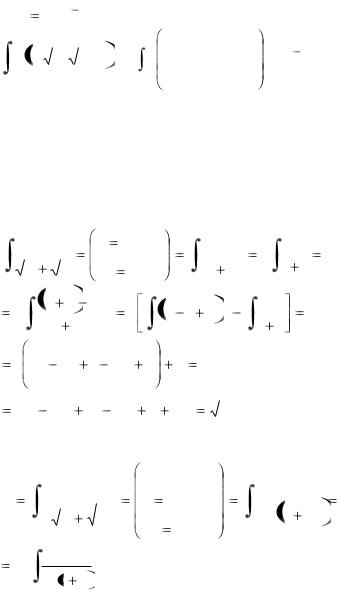
dx |
Nt N 1dt и |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
N |
|
N |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
R x, m |
|
, n |
|
,... dx = R t N , t m , t n ,... Nt N 1dt |
||||||||||
x |
x |
|||||||||||||
Так |
как все числа N, |
N |
, |
N |
|
,... ; N-1 – целые, то |
||||||||
m |
n |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
подынтегральная функция не содержит дробных степеней t, т.е. является дробно – рациональной функцией от t.
Пример 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
dx |
|
|
x t6 |
|
6t5dt |
6 |
|
t3dt |
|
||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
dx 6t5dt |
|
t3 t2 |
|
t 1 |
|||||||||||||
|
|
x |
|
x |
|
|
|
||||||||||||||||||||||
6 |
|
|
t3 1 1 |
dt 6 t2 |
t 1 dt |
|
|
dt |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
t |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
1 |
|
||||||
|
|
|
t3 |
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6 |
|
|
|
|
|
|
|
|
|
t |
ln |
t 1 |
|
|
c |
|
|
|
|
|
|
|
|||||||
3 |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2t3 |
3t2 |
|
|
|
|
|
|
c; t 6 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
6t ln |
t 1 |
x |
|
|
|
|
|
|
|
||||||||||||||||||
Пример 2*: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2.5 | 10 |
|
|
|
|
|
10t9dt |
|||||||||||
J |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
x t10 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
t10 t5 t4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
x x |
x2 |
10t9dx |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
||||||
10
dt
t5 t 1
Выбранная замена свела интеграл от иррационального выражения к интегралу от рациональной дроби. Разложим дробь на простейшие.
45
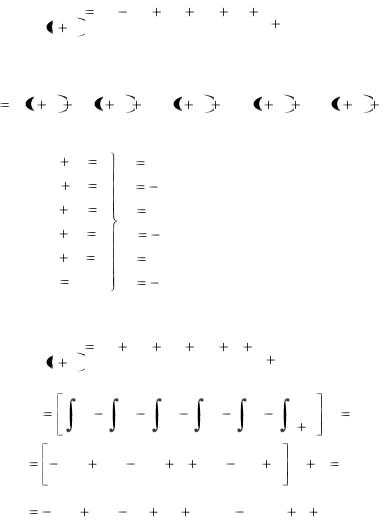
|
|
1 |
|
|
|
|
|
|
|
|
A |
|
|
|
B |
|
|
|
C |
|
|
D |
|
|
E |
|
F |
. |
|
|
|
||||||||||||||||||||||
|
t 5 t |
1 t 5 |
|
|
t 4 |
|
|
|
t 3 |
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
t |
t 1 |
|
|||||||||||||||||||||||||||||||||||||||||||
Найдем неизвестные коэффициенты: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
1 A t 1 Bt t 1 Ct 2 t 1 Dt 3 t 1 Et 4 t 1 Ft 5 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
t |
5 |
|
F |
E |
0 |
|
|
A |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
t |
|
D |
E |
0 |
|
|
B |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
t3 |
|
C |
D |
0 |
|
C |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
t2 |
|
B |
C |
0 |
|
|
D |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
t |
1 |
|
A |
B |
0 |
|
|
E |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
A |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
t0 |
|
|
|
|
|
|
|
|
F |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
t 5 t |
1 t 5 |
|
|
t 4 |
|
|
|
t 3 |
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
t t |
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
J |
|
|
|
|
|
dt |
|
|
|
|
dt |
|
dt |
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
|
dt |
10 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
t5 |
|
|
|
|
t4 |
|
t3 |
|
|
t2 |
|
|
|
t |
|
|
|
|
|
|
t 1 |
||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
1 |
|
ln |
|
t |
|
|
|
|
ln |
|
t |
1 |
|
10 |
|
|
c |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
4t4 |
|
|
3t3 2t2 |
|
|
|
|
t |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
5 |
|
|
|
|
|
10 |
|
5 |
|
10 |
|
|
10ln |
|
t |
|
|
|
10ln |
|
t 1 |
|
|
c. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
2t4 |
|
3t3 |
|
|
t2 |
|
|
|
t |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Вернемся к старой переменной
46

|
5 |
|
|
10 |
|
5 |
|
|
|
10 |
|
|
|
|
||||||||||||||||
J |
|
|
|
|
|
|
|
10ln |
10 x |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5 |
|
|
|
|
10 |
|
|
|
|
|
5 |
|
|
10 |
|
|
||||||||||||||
|
|
x |
2 |
|
x |
3 |
|
|
x |
|
x |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
10ln |
10 |
x |
|
|
1 |
|
c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2. Интегрирование выражений вида |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
R |
|
x; m |
ax |
|
b |
|
; n |
ax |
|
b |
;... |
|
|
|
|
||||||||||||
|
|
|
|
|
d |
cx |
|
d |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
cx |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ничего не изменяется по сравнению с предыдущим случаем, если все подкоренные выражения являются одной и той же дробно – рациональной функцией. В этом случае делаем замену:
|
ax |
b |
t N , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
cx |
d |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
где N – наименьшее общее кратное чисел m, n,… |
|
||||||||
Находим х: ax b cxt N |
dt N ; x |
t N d |
b |
|
t |
||||
a ct N |
|||||||||
|
|
|
|
|
|
||||
Здесь х = φ(t) – рациональная функция |
от t, поэтому |
|
t – тоже рациональная функция. Значит |
и dx |
t dt |
является рациональным выражением. Таким образом, получаем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N N |
||||
|
|
ax |
b |
|
|
|
|
|
ax |
b |
|
|
|
tNd |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
R x; m |
; n |
|
;... dx |
R |
,t m ,t m ,... t dt |
|||||||||||||||||
cx |
d |
cx |
d |
a |
ctN |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Здесь |
N |
|
, |
N |
,... |
|
|
целые |
числа. |
Поэтому получили |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
m |
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||||
интеграл от дробно – рациональной функции от t.
47
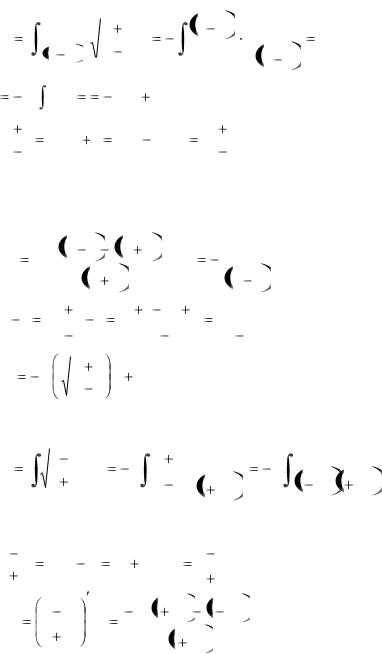
Пример 1:
|
|
|
|
|
|
|
|
|
|
|
|
t8 |
|
1 2 |
|
6t2dt |
||||
|
|
|
|
1 |
3 |
|
x 1 |
|
|
|||||||||||
J |
|
|
|
|
dx |
|
|
|
|
t |
|
|
|
|
||||||
x 1 2 |
x 1 |
|
|
4 |
|
t |
3 |
1 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
t 3dt |
|
|
|
3t 4 |
|
c. |
|
|
|
|
|
|
|
||||
2 |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x 1 |
t 3; x 1 xt3 |
t 3; x |
t3 |
1 |
; |
|
|
|
|
|||||||||||
x 1 |
|
t3 |
1 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
3t 2 |
t 3 |
|
1 t 3 |
|
1 3t 2 |
|
|
|
|
|
|
|
|
6t |
2dt |
|
|
|
|
||||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|||
|
|
|
|
|
|
|
|
|
|
t 3 |
1 2 |
|
|
|
|
|
|
|
|
|
|
t 3 |
1 2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x |
1 |
|
|
|
t 3 |
1 |
1 |
|
t 3 1 |
t 3 |
1 |
|
|
|
2 |
|
; |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
t 3 |
|
|
|
|
|
|
|
|
t 3 |
|
|
|
|
|
|
|
|
t 3 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
|
|
|
3 |
|
3 |
|
x |
1 |
|
|
|
c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
8 |
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t2dt |
|||||||||
|
|
|
|
|
1 |
|
|
x dx |
|
|
|
1 |
|
|
|
|
|
tdt |
|
|
|
|
|
|
||||||||||||||||||
|
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
. |
|||||||||
|
|
|
|
1 x x |
|
|
|
1 t2 |
|
|
1 |
|
t |
2 2 |
|
|
|
|
1 t2 1 t2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Была сделана замена |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 x |
|
|
t2 1 x t2 |
t2x; x |
|
|
|
1 t2 |
; |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
t2 |
|
|
|
|
|
|
|
|
||||||||
|
dx |
|
|
|
1 t2 |
|
dt |
|
|
|
2t 1 t2 |
|
|
|
|
|
1 t2 2t |
dt. |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
t2 |
|
|
|
|
|
|
|
1 |
|
t |
2 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
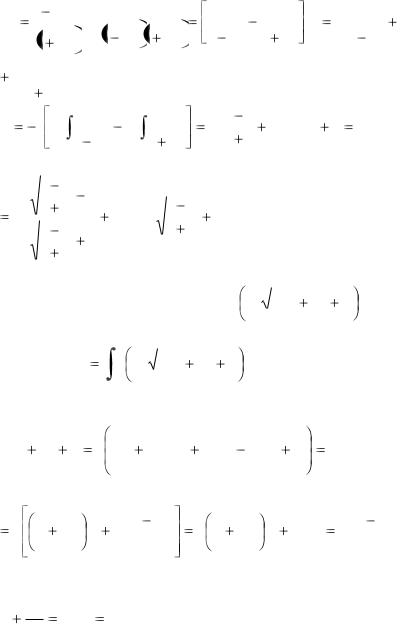
dx |
|
|
|
4tdt |
|
; |
|
|
t2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
1 |
|||||||||||
1 |
t |
2 2 |
|
1 t 2 1 t 2 |
|
|
1 t 2 |
|
|
|
|
1 t 2 |
|
2 2 1 t 2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 1 |
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
|
dt |
|
1 |
|
|
dt |
|
|
|
|
t |
1 |
|
|
|
|
|
|
|
|||||||||||||||
J |
4 |
|
|
|
|
|
|
|
|
ln |
|
|
2arctgt |
c |
|
|||||||||||||||||||||||||||
2 |
1 |
|
t 2 |
2 1 |
|
t 2 |
|
|
|
t |
1 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ln |
|
1 |
|
x |
|
2arctg |
|
1 |
x |
|
c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
3. Интегрирование выражений вида R |
|
x, |
|
ax2 |
|
bx |
|
c |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Интеграл |
|
|
J |
|
|
|
R |
x, |
ax2 |
|
bx |
|
c dx |
|
преобразуем |
к |
||||||||||||||||||||||||||
новой переменной, предварительно выделив полный квадрат:
ax2 bx c a x 2 |
2 |
b |
x |
|
b2 |
|
|
|
b2 |
|
c |
|
|
|||||
2a |
|
4a 2 |
|
|
4a 2 |
|
a |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
b |
2 |
4ac |
b2 |
|
|
|
|
|
b |
2 |
|
|
|
4ac b2 |
|||
a x |
|
|
a x |
|
|
|
D; D |
|||||||||||
2a |
|
4a 2 |
|
|
|
|
2a |
4a |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Полагаем:
b
x z; dz dx. 2a
Тогда, если
49
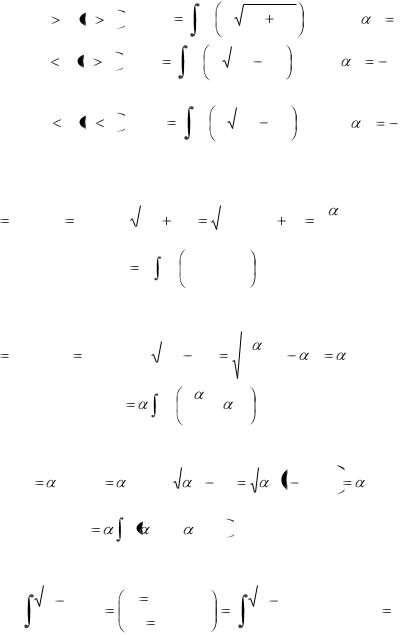
|
|
1. D |
0 |
|
a |
0 , |
то |
|
J |
|
R |
|
|
|
|
z, z 2 |
α 2 |
|
dz, где 2 |
D |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
2. D |
0 |
|
a |
0 , |
то J |
R |
z, |
|
z 2 |
a 2 |
|
dz, где |
D |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
|
|
3. D |
0 |
|
a |
0 , |
то |
J |
R |
|
|
z, |
|
|
|
α 2 |
z 2 |
dz, где |
D |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученные интегралы рационализируются, например, |
||||||||||||||||||||||||||||||||||||||||||||
с помощью тригонометрических подстановок: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
adt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
z |
atgt; dz |
|
; |
|
z 2 a 2 |
|
|
|
|
a 2 (tg |
2t |
1) |
|
|
|
|
|
|
|
|
. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
cos2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cost |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
J |
|
a |
|
R1 |
atgt, |
|
|
|
a |
dt |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cost |
cos2 t |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
a sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z |
|
; dz |
|
|
|
dt; |
|
z 2 |
|
a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
tgt |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
cost |
|
|
|
cos2 t |
|
|
|
|
|
|
|
|
|
|
cos2 t |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
J |
|
|
R |
|
|
|
|
, |
|
tgt |
dt sin t |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
cost |
|
|
|
|
|
|
|
|
|
|
|
|
cos2 t |
|
|
|
|
|
|
|
|
|
||||||||
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
z |
|
sint; dz |
|
|
costdt; |
2 |
|
|
z 2 |
2 1 |
|
|
sin2 t |
|
cost |
|||||||||||||||||||||||||||||
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
|
R |
sint, |
|
cost |
|
costdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
x |
2sint |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
4 |
x |
|
|
|
dx |
|
|
|
|
|
|
|
4 |
4sin t |
2costdt |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
2costdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4sin2 t |
|
|
|
|
|
|
|
|
|
|||||||||||
50
