
Интегральное исчисление функции одной переменной. Дурова В.Н., Зайцева М.И
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
В.Н. Дурова М.И. Зайцева В.Н. Макаров
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Учебное пособие
Воронеж 2002
УДК 517.2 Дурова В.Н., Зайцева М.И., Макаров В.Н.
Интегральное исчисление функции одной переменной: Учебное пособие / Воронеж: Воронеж. гос. ун-т, 2002. 122 с.
Пособие содержит следующие разделы: неопределенный и определенный интегралы, приложения определенных интегралов и приближенное вычисление определенных интегралов
Учебное пособие предназначено для студентов высших учебных заведений, обучающихся по направлению 652100 «Авиастроение», специальности 130100-«Самолето-и вертолетостроение» по дисциплине «Высшая математика» и соответствует образовательному стандарту по указанной специальности.
Учебное пособие подготовлено на магнитном носителе в текстовом редакторе MS WORD 97.0 и содержится в файле «Интегрирование. rar.»
Табл.1. Ил. 53. Библиогр.: 5 назв.
Научный редактор д-р физ.-мат. наук В.Д.Репников
Рецензенты: кафедра математики и физики Воронежского военного института радиоэлектроники; д-р физ.-мат. наук В.А.Родин
Печатается по решению редакционно-издательского совета Воронежского государственного технического университета
©Дурова В.Н., Зайцева М.И., Макаров В.Н., 2002
©Оформление. Воронежский государственный технический университет, 2002
2
ВВЕДЕНИЕ
В данном учебном пособии изложены лекции по интегральному исчислению функции одной переменной. Обычно этот материал изучается во втором семестре технических вузов. Подбор тем и содержание лекций соответствует образовательному стандарту специальности 130100-«Самолето-и вертолетостроение» дневной формы обучения. В связи с этим пособие содержит следующие разделы: комплексные числа, неопределенный и определенный интегралы, приложения определенных интегралов и их приближенное вычисление. При работе над пособием, в той или иной степени, была использована литература, указанная в прилагаемом списке.
Авторы стремились сочетать простоту и наглядность изложения материала с достаточной для инженера математической строгостью. В тех случаях, когда доказательность вступала в противоречие с наглядностью, предпочтение отдавалось последней. Ряд вопросов приводится без доказательства. Часть из них достаточно будущему инженеру знать на интуитивном уровне. Доказательство других вопросов, например, интегрирование дифференциальных биномов и использование подстановок Эйлера желающие могут найти в литературе, список которой прилагается.
Поскольку пособие должно быть полезным и для тех, кто по различным причинам вынужден самостоятельно изучать материал, в пособии приводятся подробные решения типичных задач.
3

1.КОМПЛЕКСНЫЕ ЧИСЛА
1.1.Определение комплексных чисел
Понятие комплексного числа возникло в связи с необходимостью решать квадратные уравнения при любых значениях дискриминанта , в том числе и отрицательных(XVIв):
x2+4x+13=0 |
D1= 4 13=-9. |
При этом возникает необходимость расширения понятия числа, необходимость введения чисел более общей природы. Действительно числа уже будут частным случаем этих «новых» чисел.
Комплексным числом называется выражение z =x+iy, где x и y – действительные числа, а i – символ, который называется мнимой единицей: i2= 1.
Корни приведенного уравнения можно записать в виде
z1 = (2+3i ), z2 = (2 3i ).
Числа х и y называются, соответственно, действительной и мнимой частями комплексного числа z и обозначаются символами:
x = Re z , y = Im z
Если y = 0, z = x + i0 считается совпадающим с действительным числом x. Если x = 0, то z = 0 + iy обозначается просто iy и называется чисто мнимым числом.
Выберем на плоскости декартову прямоугольную систему координат и будем рассматривать упорядоченную пару чисел (x,y) как координаты точек этой плоскости.
Тогда каждому числу z = x + iy будет отвечать определѐнная точка z (x,y) плоскости и, наоборот, каждой точке плоскости будет отвечать определѐнное число z = x + iy.
4
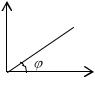
Таким образом, между множеством комплексных чисел и множеством точек плоскости Оху существует взаимно
однозначное соответствие. |
|
|
|
|
|
|
|||
Плоскость |
Оху |
называется |
|
у |
|
|
|
||
плоскостью комплексных чисел |
|
|
|
|
|||||
|
|
|
|
z(x,у) |
|||||
(z). |
Действительные |
числа |
|
|
|
|
|||
|
r |
|
|
у |
|||||
изображаются при этом точками |
|
|
|
||||||
|
|||||||||
|
|
|
|
|
|||||
оси |
Oх. Ось |
Oх |
называется |
0 |
|
|
|
x |
|
|
|
|
|||||||
|
|
|
|||||||
действительной осью. |
x |
|
Рис.1.
Чисто мнимые числа z = iy изображаются точками на оси Oу, которая называется мнимой осью.
1.2.Три формы записи комплексного числа
1.Алгебраическая форма:
z = x + iy. |
(1) |
Два комплексных числа z1 = x1 + iy1 |
и z2 = x2 + iy2 равны |
друг другу (z1 = z2) тогда и только тогда, когда x1 = x 2, и y1 = y2
Если x2 = x1, а y2 = -y1, то комплексные числа z1 = z2 называются взаимно сопряжѐнными:
z = x + iy, z = x – i y.
Точки z(x,y) и z(x,-y) симметричны относительно действительной оси Oх.
2. Тригонометрическая форма.
Введѐм в рассмотрение радиус-вектор точки z и угол φ, образованный им с положительным направлением оси Oх.
(рис.1).
5

Величины r и φ называются, соответственно, модулем и аргументом комплексного числа z и обозначаются символами:
r = | z |; φ = Arg z .
Модуль комплексного числа определяется однозначно формулой (из треугольника, рис 1);
r = | r | 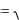
 x 2 y 2
x 2 y 2
Все значения аргумента φ удовлетворяют соотношению
tg |
y |
|
|
||
x |
||
|
Угол φ называется аргументом комплексного числа z:
Arg z( |
Arg z |
) |
Аргумент определяется не однозначно, а с точностью до числа, кратного 2π. Если z =0, то аргумент произволен.
Наименьшее по модулю значение аргумента Arg z называется его главным значением:
|
arg z |
или 0 |
2 |
|
|
|
Главное значение аргумента определяется однозначно. |
||||||
Очевидно: |
|
|
|
|
|
|
Arg z arg z 2k |
. |
k |
0, 1, 2,... |
|
|
|
Из треугольника: |
x = |
| z | cosφ и y = |
| z | sinφ . Поэтому |
|||
любое |
комплексное |
|
число |
можно |
записать |
в |
тригонометрической форме: |
|
||||
|
z |
x iy |
| z | cos |
i | z | sin |
или ( | z | =r) |
|
z |
r cos |
i sin |
|
(2) |
|
|
|
|
|
|
Два комплексных числа z1 и z2 равны тогда и только тогда, когда равны их модули, а аргументы равны или отличаются на 2кπ:
z1 z2 |
z1 |
|
z2 |
; 1 |
2 2k |
k 0, 1, 2,... |
Для перехода от алгебраической формы (1) к тригонометрической (2) пользуются равенствами:
6

|
|
|
|
|
y |
|
|
|
x |
|
|
|
|
|
y |
|
|
.. |
z |
|
|
x 2 y 2 ; tg |
cos |
|
|
|
; sin |
|
|||||||||
|
|
|
|
|
||||||||||||||
|
|
x |
|
|
z |
|
|
|
|
z |
|
|
||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Примеры: |
|
|
|
|
|
Записать |
|
комплексные |
|
|
числа |
в |
|||||||||||||||||
|
|
|
|
|
|
|
|
у |
||||||||||||||||||||||
тригонометри- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ческом виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2= i |
|
|
|
|
|
|
|
||||||||
|
1.z1 |
1 |
x |
|
1; y |
0; |
0 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
z |
|
|
12 |
|
02 |
1, |
|
|
|
-1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
1 cos0 |
i |
sin 0 . |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-i |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.z2 |
i, x |
|
0; y |
1; |
z |
|
1, |
|
2 |
, i |
1 cos |
2 i |
|
sin |
2 . |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3.z3 |
1, |
x |
|
|
|
1; y 0; |
z |
|
1, |
|
, |
1 |
1 cos |
i sin . |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4.z4 |
i, |
x |
|
0; y |
|
|
1; |
z |
|
1, |
|
|
2 , |
i |
1 cos |
2 |
|
|
i sin |
2 . |
||||||||||
3. Показательная форма. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Рассмотрим |
|
показательную |
функцию |
|
с |
мнимым |
|||||||||||||||||||||||
показателем ei . Положим по определению:
ei = cosφ - i  sin
sin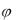 - (формула Эйлера) (3)
- (формула Эйлера) (3)
Вывод этой формулы содержится в теории рядов. С еѐ помощью от тригонометрической формы (2) записи комплексного числа можно перейти к показательной:
|
|
z rei |
|
(4) |
||
Примеры: Записать комплексные числа в показательной |
||||||
форме. |
|
|
|
|
||
1 ei0 ; i ei |
|
; 1 ei |
|
i |
|
. |
2 |
; i e |
2 |
||||
7

Правая часть формулы (3) есть комплексное число с модулем, равным 1:
у |
|
|
|
z |
ei |
; |
(5) |
|
|
|
|
|
ei |
|
cos2 |
sin2 |
|
i |
|
z |
|
|
1 |
|||
|
|
|
|
|
|
|
|
|
х
1
. Рис. 3.
При φ=0 z= e
Значит, равенство (5) на плоскости (z) определяет окружность единичного радиуса с центром в начале координат.
i0 =1; при φ=π/2 z= ei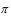 / 2 =I и т.д. Таким
/ 2 =I и т.д. Таким
образом, при изменении φ от 0 до 2π точки z |
= ei |
опишет |
||||||
окружность единичного радиуса против часовой стрелки. |
|
|||||||
В отличии от функции e x , функция ei |
периодическая с |
|||||||
периодом T = 2π. |
|
|
|
|
|
|
|
|
ei 2 |
cos |
2 |
i sin |
2 |
cos |
i |
sin |
ei |
1.3. Действия над комплексными числами
На множестве комплексных чисел определены те же действия, что и на множестве действительных чисел. Пусть
|
z1 |
x1 |
i y1 и z2 |
x2 |
i y2 |
|
а) Сумма и разность двух комплексных чисел |
||||||
определяется следующим образом: |
||||||
|
z1 |
z2 |
x1 x2 |
i y1 |
y2 |
|
т.е. при сложении комплексных чисел их действительные и мнимые части складываются, а при вычитании вычитаются.
2 3 i
i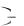 5 i
5 i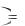 3 2
3 2  i
i
8

б) Произведение двух комплексных чисел получается по правилу умножения многочленов, учитывая, что i2 = -1:
z1z2 |
|
x1 |
i y1 x2 |
i y2 |
|
|
|
|
|
|||||
|
x1x2 |
y1y2 |
i x1y2 |
|
x2 y1 |
|
|
|
|
|
||||
Если комплексные числа заданы в тригонометрической |
||||||||||||||
форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 |
r1 cos 1 |
i |
sin |
1 |
|
, z2 |
r2 cos |
2 |
i sin |
2 , |
|||
(6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r1r2 cos |
1cos 2 - sin 1sin |
2 |
i sin |
1 cos |
2 |
cos |
1 sin 2 |
|||||||
или z1z2 |
r1r2 cos |
1 |
2 |
|
i |
sin |
1 |
2 . |
|
|
|
|||
здесь |
z1z2 |
|
r1r2 и Argz1z 2 |
|
Argz1 |
Argz2 |
|
|
||||||
Модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей.
В показательной форме: z1z2 r1r2ei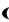 1
1 2
2 
в) Деление комплексных чисел вводится как операция, обратная умножению:
|
z |
|
|
|
|
1 |
z1 |
, если zz2 |
z1 z 2 |
0 |
|
|
z2 |
||||
|
|
|
|
|
|
В алгебраической форме: |
|
||||
|
z1 |
|
x1 |
iy1 |
|
x1 |
iy1 x2 |
iy2 |
; |
|
|
|
|
|
|
|
|
|
|
||
|
z2 |
|
x2 |
iy2 |
|
x2 |
iy2 x2 |
iy2 |
||
|
z1 |
|
x1x2 |
y1 y2 |
i y1x2 |
x1 y 2 |
||||
|
z2 |
|
|
|
|
x 2 |
y 2 |
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
Пример: |
Вычислить: |
|
|
|
||||||
9

3 |
2i |
3 |
|
2i 4 |
|
|
|
3i |
12 9i 8i |
6 18 i |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3i |
4 |
|
3i 4 |
|
|
|
3i |
16 9 |
25 25 |
|||||||||||||
Пусть числа z1 |
и z2 заданы в тригонометрической форме |
||||||||||||||||||||||
(6). Найдѐм модуль и аргумент частного. По определению: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
z1 |
zz2 |
|
|
z1 |
|
|
|
z |
|
z2 |
|
и Arg z1 |
Arg z Arg z2 . |
|||||||||
|
Отсюда: |
|
z |
|
|
|
z1 |
|
|
и |
Arg z Arg z1 Arg z2 . |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
z |
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя.
z1 |
|
|
r1 |
cos |
1 |
2 |
i sin |
1 |
2 |
или |
||
z2 |
|
|
r2 |
|||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
z1 |
|
|
r1 |
e |
i |
1 2 |
|
|
|
|
|
|
z2 |
|
|
r2 |
|
|
|
|
|
|
|
|
|
г) Возведение комплексных чисел в натуральную степень.
Целая положительная степень комплексного числа
определяется так же, как и действительного: |
z n z z...z . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
Например: i 2 |
|
1; i 3 |
|
i 2i |
i;i 4 |
i 3i |
1; |
|
||||||||
i5 |
i4i i и т.д. В общем случае: |
|
|
|
||||||||||||
|
i4k |
|
|
|
1;i4k 1 |
i;i4k 2 |
i;i4k 3 |
i . |
|
|
||||||
Пусть число z задано в тригонометрической форме: |
||||||||||||||||
|
у |
|
|
|
|
z=1+ix |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Тогда |
z r cos |
i sin . |
|||||||
|
|
|
2 |
|
/4 |
|
|
|
|
Отсюда: |
|
|
|
|||
0 |
|
|
|
|
|
x |
|
|
z n |
r n cosn |
i sin n . |
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4. |
|
|
|
В показательной форме: |
||||||
|
|
|
|
|
|
|
|
|
z n |
r n ein |
|
|
|
|
||
10
