1237

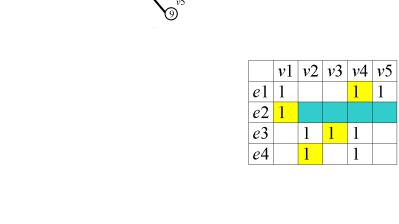
5. «ЖИЗНЕННЫЕ» ПРИЛОЖЕНИЯ ТЕОРИИ ГРАФОВ: ТЕОРЕМА О СВАДЬБАХ И ГОЛОВОЛОМКА О ВЕЧЕРИНКЕ

5.1. Трансверсаль

Рассмотрим двудольный граф Гд (E, V), где E, V – доли.

Еj – множество множеств соответствующих смежных E вершин доли [5].

Трансверсалью (или системой различных представителей или трансверсальным покрытием) называется подмножество T V, состоящее из элементов V – по одному из каждого множества Еj

(рис. 5.1).

Матрица смежности этого двудольного графа имеет вид, изображенный на рис. 5.2.

Для Гд (E,V) E = {e1, e2, e3, e4}; V = {v1, v2, v3, v4, v5}.

Множество множеств, смежных доле E вершин доли V,

Еj = {{v1, v4, v5}, {v1}, {v2, v3, v4}, {v2, v4}}.

71

Легко определить четыре трансверсали:

T1 = {v1, v2, v3, v4}, T2 = {v1, v2, v3, v5}, T3 = {v1, v3, v4, v5}, T4 = {v1, v2, v4, v5}.

Получим трансверсальные покрытия путём определения декартова произведения всех подмножеств Еj и выделения из полученных четвёрок четырёхэлементных множеств:

Еj = {{v1, v4, v5}, {v1}, {v2, v3, v4}, {v2, v4}}.

Будем указывать только номера v (рис. 5.3).

Рис. 5.3. Элементы декартова произведения подмножеств Еj, являющиеся четырёхэлементными подмножествами

Переходя к соответствующим множествам, получим четыре указанные выше трансверсали.

5.2. Теорема Холла (или теорема о свадьбах)

Теорема Холла (или теорема о свадьбах), названная в честь английского математика Филипа Холла (Philip Hall), утверждает, что если в двудольном графе любые k элементов

Возьмём вышеуказанные множества для двудольного графа (см. рис. 5.1) и будем интерпретировать их как множества знакомств некоторых юношей е с некоторыми девушками v:

Еj={{v1, v4, v5}, {v1}, {v2, v3, v4}, {v2, v4}}.

Е1={v1, v4, v5}, то есть е1 связан с тремя v; Е1 Е2 ={v1, v4, v5}, то есть е1, е2 связан с тремя v;

Е1 Е2 Е3={v1, v2, v3, v4, v5}, то есть е1, е2, е3 связан с пятью v; Е1 Е2 Е3 Е4={v1, v2, v3, v4, v5}, то есть е1, е2, е3, е4 связаны с пятью v и так далее – всего 15 возможных объединений (булеан от

4 элементов без пустого множества). Следовательно,

Всего 2 E −1 вариант.

Другой пример множества «знакомств»:

{{v1, v2}, {v1, v3}, {v2, v3}, {v1, v2, v3}, {v1, v3, v4, v5}}.

В этом случае нет трансверсали, поскольку, например, объединение четырех множеств содержит только три элемента:

Е1 Е2 Е3 Е4 = {v1, v2, v3},

поэтому соответствующий граф не разбивается на пары.

Таким образом, в данном случае объединение любых двух множеств Е должно содержать два элемента, объединение любых трёх множеств должно содержать три элемента, объединение любых четырёх множеств должно содержать четыре элемента, объединение любых пяти множеств должно содержать пять элемента (k = 5).

Что поделаешь, иногда приходится жениться на незнакомке…

5.3. Головоломка о вечеринке

Если есть свадьбы, должны быть и вечеринки! А могут быть «мальчишники», «девичники» – перед свадьбой, конечно, а не после.

Головоломка о вечеринке формулируется так: какое минимальное количество людей достаточно для того, чтобы образовать груп-

73

Обозначим красным цветом инверсное отношение (рис. 5.5). Всегда найдётся либо чёрная (отношение «быть одного пола» –

«однополость»), либо красная («разнополость») линия!

Рассмотрим отношение знакомства в группе из шести человек. Например (рис. 5.6).

Рис. 5.7. Вариант отношения знакомства в группе из пяти человек

Можно убедиться, что при любых вариантах всегда обязательно найдётся либо красный (три незнакомых), либо чёрный (три знакомых) треугольник! А вот если пять человек – это свойство не выполняется.

Например, может сложиться следующая ситуация (рис. 5.7). Здесь нет ни красного, ни чёрного треугольника. Поэтому шес-

тёрка является экстремальной (в данном случае наименьшей) характеристикой, при которой выполняется требуемое свойство – три человека либо знакомы, либо не знакомы.

75

Цветная сеть Петри – метки могут быть различных типов, обозначаемых цветами, тип метки может быть использован как аргумент в функциональных сетях.

Ингибиторная сеть Петри – возможны ингибиторные дуги, запрещающие срабатывания перехода, если во входной позиции, связанной с переходом ингибиторной дугой, находится метка.

Основными свойствами сети Петри являются:

–ограниченность – число меток в любой позиции сети не может превысить некоторого значения K;

–безопасность – частный случай ограниченности, K = 1;

–сохраняемость – постоянство загрузки ресурсов, зависящее от числа маркеров в i-й позиции и некоторого весового коэффициента;

–достижимость – возможность перехода сети из одного заданного состояния (характеризуемого распределением меток) в другое;

–живость – возможность срабатывания любого перехода при функционировании моделируемого объекта.

В основе исследования перечисленных свойств лежит анализ достижимости.

6.1. Пример сети Петри

Рассмотрим пример некоторой сети Петри (рис. 6.2).

Рис. 6.2. Некоторая сеть Петри

77

Поместим в позицию р1 метку 1 (фишку) (рис. 6.3).

Рис. 6.3. Некоторая сеть Петри с активизированной позицией р1 (а) и таблица состояний рi (б)

Теперь активизированы переходы t1 и t2. Если быстрее срабатывает t1, то фишка забирается из р1 и передается в р2 (рис. 6.4).

в

Рис. 6.4. Активирование перехода t1 (а), занесение фишки в позицию р2 (б), таблица состояний рi (в)

78

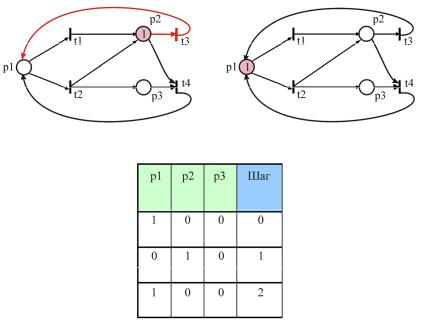
Получаем маркировку 010, возбужден только переход t3; после его срабатывания сеть возвращается к начальной маркировке 100 (рис. 6.5).

в

Рис. 6.5. Активирование перехода t3 (а), возвращение фишки в позицию р1 (б), таблица состояний рi (в)

Если же быстрее срабатывает переход t2, то фишки появляются в р2 и р3. Получаем маркировку 011, при которой возбуждены переходы t3 и t4, каждый из которых может сработать (рис. 6.6).

79

в

Рис. 6.6. Срабатывание перехода t2 (а), занесение фишек в позиции р2, р3 (б), таблица состояний рi (в)

Если срабатывает t4, то сеть возвращается к начальной маркировке: обе фишки изымаются из р2, р3 и в р1 опять оказывается «1» (рис. 6.7).

Рис. 6.7. Срабатывание перехода t4 (а), изъятие фишек из р2, р3 и возвращение фишки в позицию р1 (б), таблица состояний рi (в) (см. также с. 81)

80