
1237
.pdf
Рис. 1.14. Определение радиуса и диаметра в программе GRaph INterface (GRIN)
При нечетном числе вершин в цепи центр графа состоит из одной вершины (рис. 1.15).
Рис. 1.15. Центр простой «нечётной» цепи – вершина 2
Определение радиуса и диаметра простой «нечётной» цепи
(рис. 1.15) в программе GRaph INterface (GRIN) представлено на рис. 1.16.
Рис. 1.16. Определение радиуса и диаметра простой
«нечётной» цепи в программе GRaph INterface (GRIN)
Для цикла же Cn все вершины являются центральными
(рис. 1.17).
21

Рис. 1.17. Центр цикла – каждая вершина: 1, 2, 3
Рис. 1.18. Граф с одной центральной вершиной (вершина 1), остальные вершины являются окраиной графа
На рис. 1.18 изображен граф с одной центральной вершиной (вершина 1), остальные вершины являются окраиной графа.
Регулярный граф – граф, степени всех вершин которого равны, т.е. каждая вершина имеет одинаковое количество соседей. Степень регулярности является инвариантом графа и обозначается r(G). Для нерегулярных графов r(G) не определено. Регулярные графы представляют особую сложность для многих алгоритмов.
1.6.2. Плотность графа
Подмножество V′ вершин графа G называется кликой (Clique), если любые две входящие в него вершины смежны, т.е. порожденный подграф G(V ′) является полным.
Считается, что впервые задача о поиске максимальной клики в графе была сформулирована в 1972 году Ричардом Карпом.
Ричард Мэннинг Карп – американский учёный в области теории вычислительных систем.
22
Клика называется максимальной, если она не содержится в клике с числом вершин, большим, чем в исходной клике.
Клика называется наибольшей, если число вершин в ней наибольшее среди всех клик.
Число вершин в наибольшей клике графа G называется его плотностью
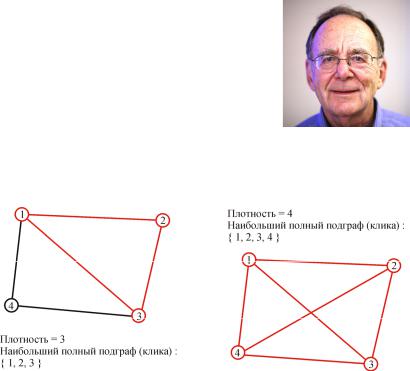
(density) или кликовым числом. Примеры даны на рис. 1.19, 1.20.
Ричард Мэннинг Карп
(англ. Richard Manning
Karp, 1935)
Рис. 1.19. Плотность графа, равная 3 Рис. 1.20. Плотность графа, равная 4
1.6.3. Покрытия, независимость, связность
Вершина покрывает инцидентные ей ребра. Ребро покрывает инцидентные ему вершины [4, 20]. Множество вершин, покрывающих все ребра, это – вершинное покрытие. Наименьшее число вершин во всех вершинных покрытиях называется числом вершинного покрытия а0 (Point – Covering Number).
Множество ребер, покрывающих все вершины, – это реберное покрытие. Наименьшее число рёбер во всех рёберных покрытиях а1
(Line – Covering Number).
На рис. 1.21 дан граф.
23

Рис. 1.21. Некоторый граф, заданный в программе GRaph INterface (GRIN), с панелью параметров типа вершин
Построим матрицу инцидентности для графа, приведенного на рис. 1.21–1.22.
Рис. 1.22. Матрица инцидентности для графа, приведенного на рис. 1.21
24
Получим покрытие вершинами ребер (вершинное покрытие): (a c)(a b)(b c) = (a bc)(b c) =
= ab ac bbc bcc = ab ac bc.
Получим покрытие ребрами вершин (рёберное покрытие):
(t1 t2 )(t2 t3 )(t1 t3 ) = (t2 t1t3 )(t1 t3 ) = = t1t2 t1t1t3 t2t3 t1t3t3 = t1t2 t1t3 t1t3.
Если вершине (ребру) поставлена в соответствие некоторая цена, возникает оптимизационная задача о наименьшем покрытии.
Независимость [20]
Подмножество V′ вершин графа G называется независимым (или внутренне устойчивым), если никакие две вершины из этого множества не смежны.
Число вершин в наибольшем независимом множестве (independent set) графа G называется неплотностью этого графа, (undensity) или числом независимости (Point – Independence Number),
или вершинным числом независимости β0.
Подмножество ребер графа G независимо, если никакие два из них не смежны.
Наибольшее число ребер в независимом множестве рёбер – реберное число независимости β1.
Числа независимости и покрытия связаны друг с другом и с количеством вершин p.
Для любого нетривиального связного графа
а0 + β0 = а1 + β1 = p.
С понятием независимости в графе связано понятие доминирования. Подмножество V′ вершин графа G будет доминирующим (или внешне устойчивым), если каждая вершина из множества V/V′ смежна с некоторой вершиной из V′.
25

Иначе говоря, каждая вершина графа находится на расстоянии 1 от доминирующего множества. Доминирующее множество называется минимальным, если никакое его собственное подмножество не является доминирующим. Доминирующее множество наименьшей мощности называется наименьшим.
1.6.4. Определение множества внутренней устойчивости орграфа
Итак, в ориентированном графе G = <V, Г>, где V – множество вершин, Г – множество дуг, подмножество S V называется внутренне устойчивым, если S∩Г(S) = , т.е. никакие две вершины из S не смежны. Пусть задан некоторый орграф [21] (рис. 1.23).
Матрица смежности этого графа имеет вид (рис. 1.24).
Рис. 1.24. Некоторый орграф |
Рис. 1.24. Матрица смежности |
|
графа, показана на рис. 1.27 |
Метод Магу нахождения максимального внутренне устойчивого множества предполагает получение по матрице смежности КНФ, описывающей условия существования такого множества, по каждой вершине, смежной другим вершинам.
Например, для заданного графа, если вершина 1 смежна вершине 2, это условие звучит так: если 1, то не 2: (1→не2).
Это эквивалентно (не 1 или не 2)
26

Если 2, то не 3, и если 2, то не 4: (2→не3)(2→не4). Это эквивалентно (не 2 или не 3) (не 2 или не 4)
Вершине 3 смежных нет – пропускаем её. Вершине 4 смежных нет – пропускаем её.
Если 5, то не 3: (5→не3). Это эквивалентно (не 5 или не 3). Запишем формулу:
(1 2)(2 3)(2 4)(5 3)
Получим ДНФ, используя распределительный закон:
(2 134)(5 3) = (25 23 1345 134)
По закону поглощения получаем:
(25 23 134)
Эта запись означает, что получены следующие множества: 1 конъюнкция – не 2 и не 5 – значит, множество {1,3,4}, 2 конъюнкция – не 2 и не 3 – множество {1,4,5}, 3 конъюнкция – не 1 и не 3 и не 4 – множество {2,5}.
1.6.5. Нахождение множества внешней устойчивости орграфа
Итак, в ориентированном графе G=<V, Г>, где V – множество вершин, Г – множество дуг, подмножество Т V называется внешне устойчивым, если для любой вершины vi из Т T∩Г(vi)# , т.е. из любой вершины, не принадлежащей Т, исходит, по крайней мере, одна дуга в Т.
Метод Магу нахождения минимального внешне устойчивого множества предполагает получение КНФ, описывающей условия существования такого множества, по каждой вершине, смежной другим вершинам [21].
Например, для заданного графа (рис. 1.23) вершина 1 смежна вершине 2, то это условие звучит так: 1 или 2.
27

Вершина 2 смежна 3 и 4: (2 или 3 или 4). Вершине 3 смежных нет – записываем 3. Вершине 4 смежных нет – записываем 4. Вершина 5 смежна 3: (5 или 3).
Запишем формулу:
(1 2)(2 3 4) 3 4(5 3)
Упрощаем:
(1 2) 3 4 = 134 234
Таким образом, получаем два минимальных внешне устойчивых множества:
{1,3,4},{2,3,4}.
1.6.6. Число вершинной связности
Числом вершинной связности Hi(G) графа G (или просто числом связности) называется наименьшее число вершин, удаление которых из G приводит к несвязному или одновершинному графу.
В программе GRaph INterface (GRIN) это почему-то названо вершинным покрытием (рис. 1.25).
Рис. 1.25. Число вершинной связности, равное 3
28

1.6.7. Пример исследования графа
Пусть задан некоторый орграф (рис. 1.26).
Рис. 1.26. Некоторый орграф
Определение покрытий
Создадим граф в программе GRIN (рис. 1.27):
Рис. 1.27. Задание графа (см. рис. 1.26) в программе GRIN
Вводим названия вершин (рис. 1.28).
Рис. 1.28. Введение буквенных обозначений вершин графа (см. рис. 1.26)
29

И тут выясняется, что вершинное покрытие неактивно для орграфа. Будем строить его вручную. Вводим обозначения рёбер
(рис. 1.29).
Рис. 1.29. Введение буквенных обозначений рёбер графа
(см. рис. 1.26)
Получим таблицу покрытий (рис. 1.30).
Рис. 1.30. Таблица покрытий – определение вершинного покрытия
На предыдущем занятии мы рассмотрели вершинное покрытие – это число α0, в данном случае необходимо две вершины – В и Е, то есть α0 = 2 (рис. 1.31).
30
