1237

Рис. 1.31. Таблица покрытий – определение рёберного покрытия (это число α1)

Наименьшее число рёбер, покрывающих все вершины, – рёберное покрытие α1, в данном случае необходимы три ребра, то есть

α1 = 3.

Исследование орграфа на устойчивость

Запишем логическое выражение по методу Магу для рис. 1.28:

(A → B) (B → C) (B → D) (E → C).

Преобразуя, получим:

(A B) (B C) (B D) (E C).

Вводим выражение в Logic Converter (рис. 1.32).

Рис. 1.32. Ввод логического выражения в Logic Converter

31

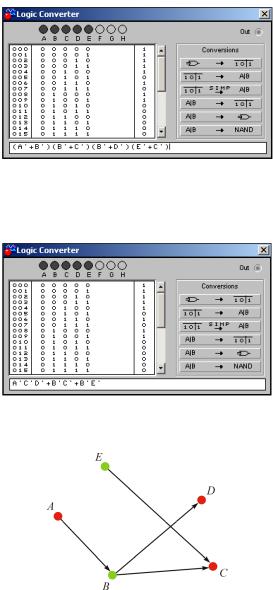
Получаем таблицу истинности (рис. 1.33).

Рис. 1.33. Получение таблицы истинности для логического выражения в Logic Converter

Затем минимизируем (рис. 1.34).

Рис. 1.34. Минимизация логического выражения в Logic Converter

Получили: A’C’D’ – это значит B, E (рис. 1.35).

Рис. 1.35. Независимые вершины B, E

32

Далее: B’C’ – это значит A, D, E (рис. 1.36).

Рис. 1.36. Независимые вершины A, D, E

И, наконец, B’E’ – это значит A, C, D (рис. 1.37).

Рис. 1.37. Независимые вершины A, C, D

Таким образом, число вершинной независимости β0 = 3. Теперь определим число рёберной («дужной» – у нас орграф!) независимости β1.

Для этого обозначим рёбра буквами, опять-таки для использо-

вания Logic Converter (рис. 1.38).

Рис. 1.38. Граф, изображенный на рис. 1.26, с новыми буквенными обозначениями рёбер

33

Видно, что максимум не смежны A и D (C или D), то есть β1 = 2. Определим число независимости β1 с помощью Logic Converter.

Запишем логическое выражение по методу Магу для рис. 1.38:

(A → B C)(С→ B)(B → C D)(D → B).

Преобразуя, получим:

(A B C)(С B)(B C D)(D B).

Вводим логическое выражение в Logic Converter (рис. 1.39, 1.40).

Рис. 1.39. Ввод логического выражения в Logic Converter

Рис. 1.40. Минимизация логического выражения в Logic Converter

34

Например, A’B’ – это C, D

B’C’ – это AD, A’C’D’ – это всего одна дуга. Следовательно, максимальное значение равно двум, β1 = 2:

β0 = 3, β1 = 2, α1 = 3, α0 = 2.

Проверим:

α0 + β0 = 2 + 3, α1 + β1 = 3 + 2.

Вроде, сходится!

Нахождение множества внешней устойчивости орграфа

Запишем логическое выражение по методу Магу для графа на рис. 1.28:

(A B) (B C D) C D (E C).

Введём это выражение в Logic Converter (рис. 1.41).

Рис. 1.41. Ввод логического выражения внешней устойчивости в Logic Converter

35

Минимизируем (рис. 1.42).

Рис. 1.42. Минимизация логического выражения внешней устойчивости в Logic Converter

Получили:

(A B) C D = A C D B C D,

т.е. подмножества на рис. 1.43, или на рис. 1.44.

36

2. РЕШЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ НА ГРАФАХ

Другая экстремальная задача – задача нахождения кратчайшего пути в графе (не цикла, как в задаче Гамильтона!) может быть решена с помощью алгоритма Дейкстры (Dijkstra’s algorithm) – алгоритма, предложенного нидерландским ученым

культет теоретической физики Лейденского университета. В 1951 году увлёкся программированием, поступил на трёхнедельные компьютерные курсы в Кембридже, с 1952 года работал программистом в Математическом центре Амстердама.

Уже в 1952 году принял решение окончательно специализироваться на программировании, но курс теоретической физики окончил. В 1956 году принял участие в разработке ЭВМ X1. Эта машина была создана тремя энтузиастами за год. Именно для оптимизации разводки плат для X1 был придуман алгоритм поиска кратчайшего пути на графе, известный как «алгоритм Дейкстры».

В 1957 году Дейкстра женился. Как вспоминал он сам, в графе «профессия» анкеты, которую положено заполнять при бракосочетании, он написал «программист», и его заставили переписывать доку-

37

менты, заявив, что такой профессии не существует. В результате, как писал Дейкстра, «хотите – верьте, хотите – нет, но в графе „профессия“ моего свидетельства о браке значится забавная запись „физик-теоретик“!».

Когда советское правительство приняло решение о переходе советской промышленности к копированию модельного ряда IBM/360, Дейкстра (работавший в то время в конкурировавшей с IBM фирме Burroughs) назвал это решение величайшей победой

Запада в холодной войне, а выбранную для клонирования модель IBM/360 (прообраз советской ЕС ЭВМ) – величайшей диверсией Запада против СССР.

Алгоритм Дейкстры в принципе соответствует концепции динамического программирования Беллмана – одного из подхода к сокращению перебора вариантов.

Ричард Эрнст Беллман – американский математик, один из ведущих специалистов в области математики и вычислительной техники.

2.1.Нахождение кратчайшего пути в графе

срёбрами единичной длины

Вспомним разметку графа задачи о Ханойской башне для n = 2 (рис. 2.1) для определения кратчайшего пути из исходной вершины с координатами (0,1/2) в целевую (1/2, 0). В этом графе все рёбра имеют единичную длину, т.е. это задача определения кратчайшего пути в графе с рёбрами единичной длины.

Целевую вершину помечаем индексом 0, это значит, что при её достижении задача решена (рис. 2.2).

Смежные вершине с индексом 0 вершины приобретут индекс 1, смежные вершинам с индексом 1 вершины приобретут индекс 2, смежные вершинам с индексом 3 вершины приобретут индекс 3, и процесс разметки закончится – все вершины имеют индексы. Индекс

38

исходной вершины равен 3, это значит, что кратчайший путь из этой вершины в целевую (с индексом 0) имеет длину 3. Кратчайший путь находят путём движения из исходной вершины в направлении уменьшения (на 1) индекса (рис. 2.3).

Рис. 2.3. Кратчайший путь в графе задачи о Ханойской башне для n = 2

39

Также может быть найден кратчайший путь из любой другой вершины в целевую, имеющую индекс 0.

Решим задачу о Ханойской башне (рис. 2.4) с помощью программы GRaph INterface (GRIN). Создаём граф задачи о Ханойской башне (для n = 2).

Рис. 2.4. Графе задачи о Ханойской башне для n = 2, построенный в GRaph INterface (GRIN)

Задаём: Свойства – Сеть – Кратчайший путь, получаем решение

(рис. 2.5).

Рис. 2.5. Решение задачи о Ханойской башне для n = 2 в GRaph INterface (GRIN)

40