1237

Условия для инициализации, приращения, завершения и прочие помещаются внутри символа в начале или в конце в зависимости от типа цикла. Символы могут быть вычерчены в любой ориентации, но предпочтительной является горизонтальная ориентация.

Внутрь символа помещают обозначения или описания операций. Символы могут быть отмечены идентификаторами или порядковыми номерами.

Идентификатор представляет собой букву или букву с цифрой и должен располагаться слева над символом.

Направления линий связи слева направо и сверху вниз считаются стандартными, и линии связи изображаются без стрелок, в противоположном случае – со стрелками.

Линии могут соединяться одна с другой, но не могут разветвляться.

Реализация схемы алгоритма конечным автоматом

Схемы алгоритмов и графы переходов используются в теории алгоритмов и автоматов. Для задания простейших управляющих автоматов нам понадобятся символы начала и конца алгоритма, процессы, решения, линии, соединители и, возможно, комментарии.

Символом процесса будем кодировать самые элементарные действия – z, это будем называть микрооперациями. Несколько микроопераций в одном процессе (в процессе может быть одна или несколько z, говорят: «выполняемых в одном такте») называют микрокомандой. Символом решения будем кодировать логические условия – одну логическую переменную. Тогда вся схема алгоритма – микропрограмма. Реализация графа специального вида – схемы алгоритма конечным автоматом – подробно изложена в [3, 4].

Более сложные символы используются в программировании и пригодятся вам для курсовых работ и дипломного проектирования.

91

8. ПРИЛОЖЕНИЯ ТЕОРИИ ГРАФОВ В ТЕОРИИ ГРУПП

Теория групп, о которой уже шла речь в предыдущих учебных дисциплинах, широко используется в настоящее время в криптографических алгоритмах шифрования, в помехоустойчивом кодировании и др. Поэтому рассмотрим, как связана теория графов с этой теорией.

8.1. Группа S3

Как известно из курса дискретной математики, для трех элементов х1, х2, х3 существуют шесть вариантов последовательностей – перестановок:

х1х2х3, х2х3х1, х1х3х2, х3х1х2, х2х1х3, х3х2х1.

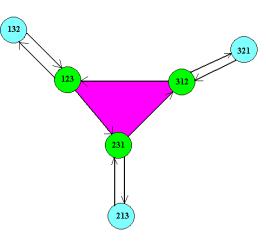
Изобразим граф перестановок, которые обозначим 123, 231, 132, 312, 213, 321 в виде (рис. 8.1).

Рис. 8.1. Граф перестановок 123, 231, 132, 312, 213, 321

На рис. 8.1 вершины 123, 231, 312 образуются путём циклического сдвига влево последовательности 123, вершины 132, 321, 213

92

получены путём перестановок последних двух позиций соответст-

вующих кодов 123, 231, 312.

Если соединить вершины 132, 321, 213, получим ещё один цикл

(рис. 8.2).

Рис. 8.2. Граф перестановок 123, 231, 132, 312, 213, 321

с внешним циклом

Также можно ввести ещё дополнительные дуги, связывающие, например, 213 и 123, – это перестановки первых двух позиций и т.д.

Запишем порождение вариантов перестановок следующим образом:

x1x2 x3 .

x2 x3 x1

Эта запись означает, что х1 переходит (отображается) в х2, х2 – в х3, х3 – в х1.Обозначим возможные подстановки:

93

Произведением подстановок назовем последовательное выполнение сначала первой, а затем второй из перемножаемых подстановок. Подстановка Θ – это нейтральный элемент или единица по умножению.

Таким образом, имеем алгебру <П, >, где П – множество подстановок {Θ,1,2,3,4,5}, « » – бинарная операция П П П или П2 П.

Очевидно, что умножение на нейтральный элемент Θ приводит к тому же номеру перестановки: Θ i=i, в частности, Θ Θ=Θ.

Получим вторую строку таблицы умножения:

94

Получим четвёртую строку таблицы умножения:

95

Получим пятую строку таблицы умножения:

Получим последнюю, шестую строку таблицы умножения:

96

Как было показано в курсе дискретной математики, такая алгебра является группой.

Иногда перестановки записывают в виде матриц, в каждой строке которых одна единица (используется так называемый унитарный код), например 123, выглядит так:

100

010 .001

В другом виде (с использованием матриц унитарного кода) таблица умножения 6 6 выглядит так (рис. 8.3).

97

Рис. 8.3. Таблица Кэли группы с использованием матриц унитарного кода

Это называется таблица Кэли симметрической группы S3 (таблица умножения матриц перестановок).

Как видно, табл. 8.1 не симметрична относительно главной диагонали, т.е. группа не абелева (рис. 8.4).

Рис. 8.4. Несимметрия перестановок в группе S3

98

Тем не менее группа S3 называется симметрической в силу своеобразной симметрии соответствующего ей графа.

8.2. Группа S4

Имеется всего 24 перестановки четырёх элементов 1234, соответствующий граф (граф Кэли) изображён на рис. 8.5.

Рис. 8.5. Граф Кэли симметрической группы S4

Знакопеременной группой подстановок степени n (An) называется подгруппа симметрической группы Sn степени n, содержащая только чётные перестановки.

Ещё более симметрична диэдральная группа (Dn, группа диэдра) – группа симметрии правильного многоугольника, включающая

99

как вращения, так и осевые симметрии, граф «снежинка» хороший пример (рис. 8.6).

Рис. 8.6. Снежинка – графическое изображение некоторой диэдральной группы Dn

Диэдральные группы являются простейшими примерами конечных групп и играют важную роль в теории групп, геометрии, и химии.

Вот, например, как изображаются некоторые операции в такой группе для восьмиугольника – знака «Стоп» (рис. 8.7).

Рис. 8.7. Операции вращения и отражения для восьмиугольника – знака «Стоп»

Первая строка показывает восемь вращений, а вторая – восемь отражений.

Имеются также и циклические группы Сn.

100