
Дискретная математика & математическая логика
..pdf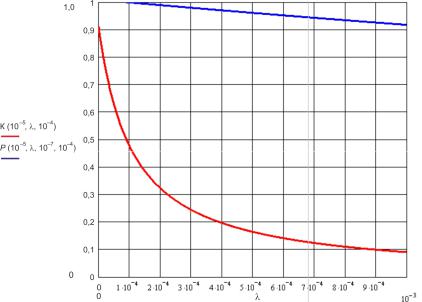
kг = |
|
|
|
φ+ δ |
|
|
|
|
|
= Р(δ, λ, φ, µ). |
||||
φ( |
φ |
+ |
|
δ |
+ |
δ |
+ |
λ |
) |
|
||||
|
|
|
|
|
||||||||||
µ |
|
φ |
|
µ |
|
|
||||||||
|
|
|
|
µ |
|
|
|
|
|
|||||
Обозначим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К(δ, λ, µ) = |
|
|
|
|
1 |
. |
||||||
|
|
|
|
|
||||||||||
|
|
1 + |
λ + δ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
µ |
|
Получим графики сравнения двух марковских цепей для
δ = 10-5 , φ = 10−7 , µ = 10−4 , λ = 0...10−3 (рис. 3.36).
Рис. 3.36. Изменение коэффициентов готовности марковской цепи
(рис. 3.33 – К и рис. 3.35 – Р; δ = 10−5 , φ = 10−7 , µ = 10−4 , λ = 0...10−3 )
111
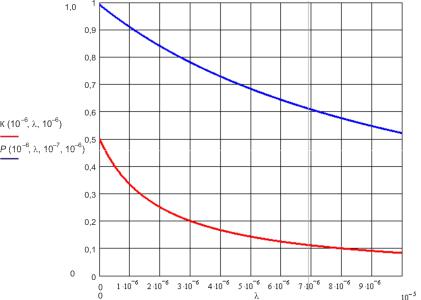
Получим графики для δ = 10-6 , φ = 10−7 , µ = 10−6 , λ = 0...10−5
(рис. 3.37).
Рис. 3.37. Изменение коэффициентов готовности марковской цепи
(рис. 3.33 – К и рис. 3.34 – Р; δ= 10−6 , φ = 10−7 , µ = 10−6 , λ = 0...10−5 )
Получим выражение для оценки вероятности нахождения в состоянии 2:
р2 = О(δ,λ,φ,µ) = |
|
|
µδ |
||
|
|
|
. |
||
|
δ |
|
|||
(µ + |
µ + δ+ λ)φ |
||||
φ |
|||||
|
|
|
|
||
Соответствующий график изображён на рис. 3.38.
112
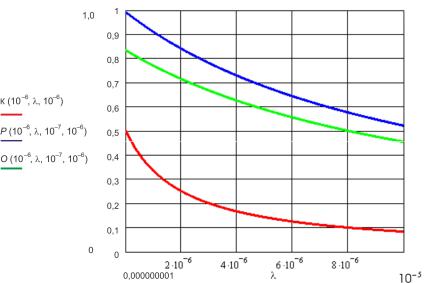
Рис. 3.38. Изменение коэффициента готовности марковской цепи (рис. 3.33 – К и рис. 3.35 – Р, О – вероятности нахождения в состоянии 2;
δ = 10−6 , φ = 10−7 , µ = 10−6 , λ = 10−9...10−5 )
3.9. ПЕРЕЧИСЛЕНИЕ ГРАФОВ
Перечисление графов может быть осуществлено, например, с использованием кодирования матриц смежности. Матрица смежности неориентированного графа без петель а – b из двух вершин:
|
a |
b |
a |
0 |
1 |
b |
1 |
0 |
Матрица смежности неориентированного графа без петель «треугольник»:
113

|
a |
b |
c |
a |
0 |
1 |
1 |
b |
1 |
0 |
1 |
c |
1 |
1 |
0 |
Матрица смежности неориентированного графа без петель «квадрат с диагоналями»:
|
a |
b |
c |
d |
a |
0 |
1 |
1 |
1 |
b |
1 |
0 |
1 |
1 |
c |
1 |
1 |
0 |
1 |
d |
1 |
1 |
1 |
0 |
Код F731 задает полуматрицу смежности полного графа без петель из пяти вершин. Матрица смежности неориентированного полного графа без петель «пятиугольник с диагоналями»:
|
a |
b |
c |
d |
e |
|
a |
0 |
1 |
1 |
1 |
1 |
F |
b |
1 |
0 |
1 |
1 |
1 |
7 |
c |
1 |
1 |
0 |
1 |
1 |
3 |
d |
1 |
1 |
1 |
0 |
1 |
1 |
e |
1 |
1 |
1 |
1 |
0 |
– |
Аналогично может быть задан и ориентированный граф. Процедура, порождающая соответствующие коды, например F731, будет перечисляющей процедурой для графов указанного числа вершин.
Перечисление графов-деревьев [9]
Теорема Кэли. Число деревьев с n вершинами, пронумерованными числами от 1 до n, nn − 2 .
Так, для n = 2 получаем 1 вариант, для n = 3 получаем 3 варианта, а для n = 4 получаем 16 вариантов – рис. 3.39.
При перечислении таких помеченных деревьев используется комбинаторное понятие «транспозиция» – перестановка, которая меняет местами только два элемента.
114
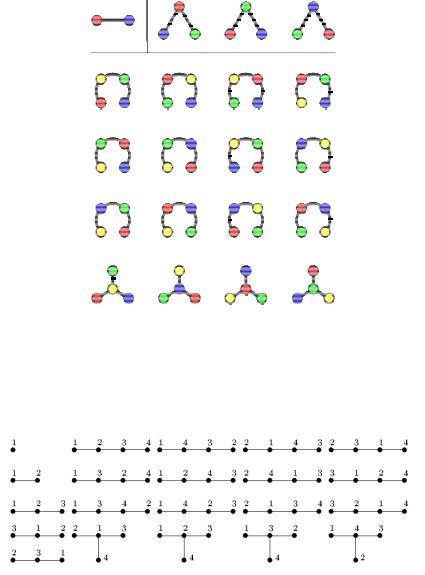
Рис. 3.39. Деревья с помеченными вершинами (2, 3, 4)
Рассмотрим сопоставление с каждым деревом некоторого кода [9]. На рис. 3.40 – 2-, 3-, 4- деревья представлены иначе, чем на рис. 3.39 – здесь указаны номера вершин:
Рис. 3.40. Деревья с помеченными вершинами (1, 2, 3 и 4)
115
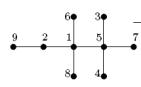
Возьмём дерево, вершины которого помечены цифрами от 1 до n. Оказывается, каждому варианту дерева с n вершинами можно сопоставить последовательность из n – 2 символов с индексами от 1 до n, обозначаемых, например, х.
Закодируем, например, дерево из 9 вершин (рис. 3.41):
Рис. 3.41. Дерево из 9 вершин
Возьмём в дереве (см. рис. 3.41) лист с минимальным номером и возьмём в качестве первого индекса номер вершины, с которой соединён это лист. Затем удалим это лист. Второй буквой будет номер вершины, с которой соединён минимальный лист в оставшемся дереве. Это лист тоже удалим и будем повторять эту операцию до тех пор, пока не останется дерево из двух вершин – ребро.
Получаем
x5 x5 x1 x5 x1 x1 x2 = x52 x1 x5 x12 x2 .
Это так называемый код (моном) Прюфера (1918), по шагам процесс кодирования дерева на рис. 3.41 представлен на рис. 3.42.
По любой последовательности длиной n – 2 можно восстановить соответствующее помеченное дерево. Степень (валентность) каждой вершины на единицу больше частоты, с которой переменная, индекс которой является номером этой вершины, встречается в этой последовательности. Вершины, номера которых не встречаются в последовательности, являются листьями.
Взяв первый элемент последовательности, проведём ребро, соединяющее лист с минимальным номером и вершину, в которой стоит индекс этого первого элемента.
116
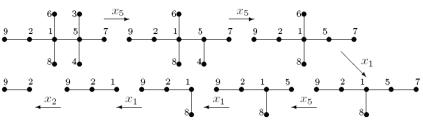
Рис. 3.42. Получение кода Прюфера для некоторого дерева
из 9 вершин: x5 x5 x1 x5 x1 x1 x2 = x52 x1 x5 x12 x2
Затем первый элемент последовательности стираем и повторяем процедуру для новой последовательности (с учётом того, что один лист уже использован, а степень вершины с номером, равным индексу первого элемента последовательности, уменьшилась на 1).
Последнее ребро соединяет две вершины, степени которых ещё не закончены.
Тем самым установлено взаимно однозначное соответствие между помеченными деревьями на n вершинах и так называемыми упорядоченными мономами в разложении выражения
(x1 + x2 + ... + xn )n−2 .
Из этого выражения получаем и выражение теоремы Кэли: (1+1+ ... +1)n−2 = nn−2 .
Второй способ подсчёта числа помеченных деревьев основан на производящих функциях.
Рассмотрим в качестве примера перечисление корневых деревьев [9].
Корневым графом называется граф с выделенной вершиной, называемой корнем, т.е. корневой граф – это пара (G, v), где G – граф, а v – некоторая его вершина. Два корневых графа называются изоморфными, если существует взаимно однозначная функция, отображающая множество вершин одного графа на множество вершин другого, которая сохраняет не только смежность, но и переводит корень одного графа в корень другого графа.
117
Пусть
∞
T (x) = ∑Tp x p
p=1
производящая функция для корневых деревьев. Таким образом, Tp представляет собой число корневых деревьев порядка p.
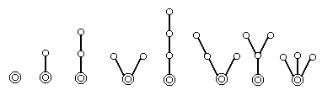
Корневые деревья 1, 2, 3, 4 показаны на рис. 3.43:
Рис. 3.43. Корневые деревья 1, 2, 3, 4
Четыре первых слагаемых производящей функции T(x) в методе Пойа даются соотношением
T (x) = x + x2 + 2x3 + 4x4 + ....
Нахождение подобных производящих функций для графов основывается на так называемой теореме перечисления Г. Пойа. Теорема стала широко известна в начале 1960-х годов, как основной инструмент для решения проблем изоморфизмов в теории графов.
118
4. ОПТИМИЗАЦИЯ
Задачей оптимизации в математике является нахождение экстремума (минимума или максимума) действительной функции в некоторой области. Иногда эти задачи называют экстремальными.
Дискретное программирование (дискретная оптимизация) – раздел математического программирования. В противоположность задачам оптимизации с непрерывными переменными, переменные
взадачах дискретного программирования принимают только дискретные значения, например целочисленные.
Задачи комбинаторной оптимизации можно решить с помощью методов дискретного программирования. Одним из основных методов решения задач дискретного программирования является метод ветвей и границ и его модификации.
Пример экстремальной задачи – нахождение максимального потока в частном классе графов – сетях (алгоритм Форда – Фалкерсона). Задача о назначениях – построение паросочетаний с минимальной суммой весов пар. Экстремальная задача на множестве перестановок – это задача коммивояжера.
Комбинаторная оптимизация – область теории оптимизации
вприкладной математике, связанная с исследованием операций, теорией алгоритмов и теорией вычислительной сложности. В комбинаторной оптимизации используются как математические подходы, так и методы искусственного интеллекта. Алгоритмы комбинаторной оптимизации, одним из наиболее популярных среди них является метод ветвей и границ, позволяют уменьшать пространство допустимых решений с помощью эффективной процедуры поиска.
119
4.1. ПОЛНЫЙ ПЕРЕБОР
Полный перебор (или метод «грубой силы», англ. brute force) – метод решения задачи путем перебора всех возможных вариантов. Сложность полного перебора зависит от размерности пространства всех возможных решений задачи.
В криптографии на сложности полного перебора основывается оценка криптостойкости шифров. В частности, шифр считается криптостойким, если не существует метода взлома существенно более быстрого, чем полный перебор всех ключей.
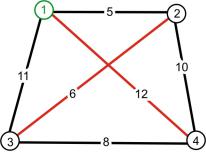
Задача коммивояжера – задача самого дешевого обхода вершин графа с возвратом в исходную вершину, например вершину 1. Граф нагружен условными единицами стоимости проезда из пункта впункт(рис. 4.1).
Рис. 4.1. Задача коммивояжера
Для полного перебора маршрутов будем строить дерево обхода вершин, каждую вершину дерева будем обозначать последовательностью из номеров уже пройденных вершин (рис. 4.2).
Таким образом, лучшие маршруты (1, 2, 3, 4, 1) и (1, 4, 3, 2, 1) «стоят» 31 условную единицу. Здесь в скобках указаны последовательности вершин графа.
«Жадный» алгоритм – алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, при допущении, что конечное решение также окажется оптимальным.
120
