Дискретная математика & математическая логика

Больше вариантов нет. Переходим к раскрытию вершины 6. Исходное положение при раскрытии вершины № 6:

–3 1

Первый вариант раскрытия вершины № 6:

Это мы получим вершину № 10. Определим эвристическую функцию для этой вершины. Не на своём месте расположены кубики 2, 1 (2). Место, которое должны занять кубики 1, 2, не заняты (0), над кубиком № 3 – нет кубиков (0), над кубиком № 2 – нет (0), над кубиком № 1 – нет (0):

231

Получаем второй вариант раскрытия вершины № 6:

Это мы получим вершину № 11. Определим эвристическую функцию для этой вершины. Не на своём месте расположены кубики 3, 2, 1 (3). Места, которые должны занять кубики 1, 2, 3, не заняты (0), над кубиком № 3 – нет кубиков (0), над кубиком № 2 – один (1), над кубиком № 1 – два (2):

= 3 + 0 + 3 = 6, а оценочная функция (это уже третий шаг!)

232

Получаем третий вариант раскрытия вершины № 6:

Это уже было – вершина № 3 (первый шаг, оценка 5), да третий шаг – получаем оценочную функцию 7.

Четвёртый вариант раскрытия вершины № 6:

Это тоже было – вершина № 5 (первый шаг, оценка 6), да третий шаг – получаем оценочную функцию 7.

Больше вариантов нет, получаем минимальное значение – вершина № 10:

Исходное положение при раскрытии вершины № 10:

Первый вариант раскрытия вершины № 10:

Тут уже всё ясно – не на своём месте только кубик № 1, и ему ничего не мешает!

233

= 1 + 0 + 0 = 1, а оценочная функция (это уже четвёртый шаг!)

Он уже был на втором шаге – у него оценочная функция была 6, станет8 (+ 2 шага).

Четвёртый вариант раскрытия вершины № 10:

Он также был – на предыдущем шаге. Оценочная функция была 9, станет 10.

Таким образом, выбираем: Вершина 12. Исходное положение:

234

Здесь достигается целевое состояние:

Задача решена. Итак, последовательность шагов такая: исходное положение:

Первый шаг:

Второй шаг:

Третий шаг:

Четвёртый шаг:

235

Пятый шаг, целевое состояние:

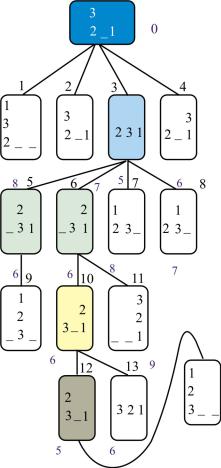
Граф решения задачи имеет вид (рис. 8.2):

Рис. 8.2. Граф решения задачи перестановки кубиков

236

Алгоритм называется гарантирующим, если для произвольного графа состояний он заканчивает работу построениям оптимального пути. Алгоритм, использующий описанные оценочные функции, является гарантирующим, если для всех вершин выполняется

положительное число.

Для сравнения разных эвристических алгоритмов используют

меньшеечисловершин.

237

9. СЛОЖНОСТЬ АЛГОРИТМОВ

Будем рассматривать временную сложность. Это функция, которая каждой входной длине n ставит в соответствие минимальное время, затрачиваемое алгоритмом на решение всех однотипных индивидуальных задач этой длины на абстрактной модели алгоритма (например, намашинеТьюринга). Времяизмеряется вчисле шагов.

Из курса математического анализа известно, что функция f (n) есть О(g(n)), если существует константа с такая, что |f (n)| ≤ c (g(n)) для всех n ≥ 0.

O(n) – сложность порядка n, n – параметр исходных данных алгоритма. O(n2 ) – сложность порядка n2 .

Сложность бывает минимальной, средней и максимальной. При построении функции сложности исходят из наиболее

худшего случая (worst-case analysis).

Например, временная сложность некоторого алгоритма на графахвзависимостиотчиславершин

T (n) = 5n2 +15n −14.

Решение задачи коммивояжёра при переборе всех комбина-

ций: Т(n) = с(n–1).

Сложностью задачи называется сложность наилучшего алгоритма.

Полиномиальным алгоритмом (или алгоритмом полиномиальной временной сложности) называется алгоритм, у которого временная сложность равна О(Р(n)), где Р(n) – некоторая полиномиальная функция от входной длины n.

Алгоритмы, для временной сложности которых не существует такой оценки, называются экспоненциальными. А(n!)?

Любая неполиномиальная функция сложности может быть представлена в виде

238

T (n) = 2 p (n) ,

где n – размерность задачи; р(n) – некоторый полином. Полиномиальные алгоритмы – « хорошие». Экспоненциаль-

ные – « плохие». Это разделение условно, так как при большой степени (более 4) полиномиальный алгоритм становится «плохим».

Задача считается труднорешаемой, если для нее не существует разрешающего полиномиального алгоритма.

Итак, основные классы сложности таковы: а) Полиномиальная сложность.

P(n) – полином от n. O(P(n)) – сложность задач класса Р. Полиномиальные задачи: степень полинома не зависит от n. Например: O(P(n)) – линейная, O(P(n2 )) – квадратичная,

O(P(n3 )) – кубическая.

б) Экспоненциальная сложность.

O(P(xn )),

класс Е – экспоненциальный.

O(P(2n )).

Например:

– построение булеана,

n

O(P(22 ));

– нахождение всех переключательных функций от n переменных. При больших n задача становится практически нерешаемой.

Асимптотические оценки сложности алгоритма

Практически нет необходимости в построении точной функции сложности, поэтому часто используют асимптотические оценки. Сравнивают поведение реальной функции f (n) и идеализированной (более простой) g(n), когда n→ ∞ .

239

Говорят, что функция f (n) = О(g(n)), если существует константа с такая, что |f (n) | ≤ c (g (n)) для всех n ≥ 0:

lim f (n) = c > 0 .

n→∞ g(n)

Пусть

T (n) = 5n2 +15n −14,

тогда

T (n) = O(n2 ),

поскольку

lim 5n2 +15n −14 = 5.

n→∞ n2

Говорят, что функция f (n) = О(g(n)), если

lim f (n) = 0.

n→∞ g(n)

Пусть

T (n) = 5n2 +15n −14,

f (n) = О(g(n)) – верхняя граница сложности, т.е. время работы алгоритма растёт не быстрее, чем g(n).

240