Дискретная математика & математическая логика

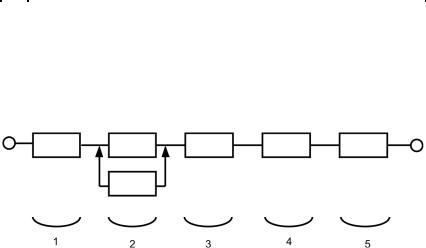
Начнём увеличивать ВБР всей системы, учитывая условие

Wс ≤ Wсзад – табл. 4.8, 4.9. Исходное: 0-й шаг – каналы: 1, 1, 1, 1, 1.

Вводим ещё один канал на каждом участке, а на первом – ещё два.

Получаем 3, 2, 2, 2, 2.

(δ1i )* = δ12 , значит, очередной элемент надо добавить на 2-м участке. Следовательно, ССНдляшагаj = 1 будетиметьвид– рис. 4.22:

Рис. 4.22. ССН для первой итерации увеличения вероятности безотказной работы

Pс1 = 0,9·0,9375·0,82·0,8·0,9 = 0,49815.

Wс1 = Wс0 + W2 = 78 < Wсзад ,

161

т.е. увеличиваем резерв только на 2-м участке, остальные без изменений. Вторая итерация – табл. 4.10, 4.11. Исходное: 1-й шаг – увеличиваем резерв только на 2-м участке, остальное без изменений. Каналы 1, 2, 1, 1, 1. 2-й шаг – опять увеличиваем резервы, в том числе и на 2-м. Получаем 3, 3, 2, 2, 2.

Таблица 4 . 1 0

Вторая итерация задачи Б

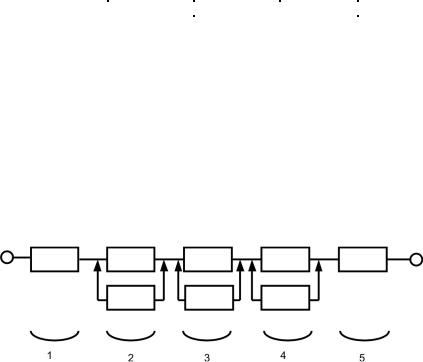
(δi2 )* = δ24 . Очередной элемент добавим на 4-м участке. Следовательно, ССН для шага j = 2 будет иметь вид (рис. 4.23):

Рис. 4.23. ССН для второй итерации увеличения вероятности безотказной работы (задача Б)

Pс2 = 0,9·0,9375·0,82·0,96·0,9 = 0,59778,

Wс2 = Wс1 + W4 = 90 < Wсзад .

162

Таким образом, увеличиваем резерв только на 4-м участке, остальные без изменений. Третья итерация – табл. 4.12, 4.13. Исходное: 2-й шаг – увеличиваем резерв только на 4-м участке, остальное без изменений. Каналы 1, 2, 1, 2, 1. 3-й шаг – опять увеличиваем резервы, в том числе и на 4-м. Получаем 3, 3, 2, 3, 2.

Таблица 4 . 1 2

Третья итерация задачи Б

Таблица 4 . 1 3

Определение наиболее выигрышного участка для 3-й итерации задачи Б

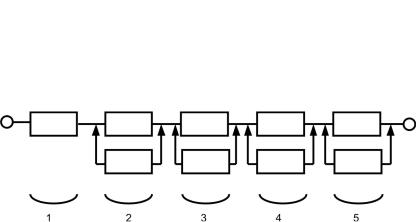
(δ3i )* = δ33 , значит, очередной элемент надо добавить на 3-м участке. Следовательно, ССНдляшагаj = 3 будетиметьвид(рис. 4.24):

Рис. 4.24. ССН для 3-й итерации увеличения вероятности безотказной работы (задача Б)

Pс3 = 0,9·0,9375·0,9676·0,96·0,9 = 0,705,

Wс3 = Wс2 + W3 = 103 < Wсзад .

163

Таким образом, увеличиваем резерв только на 3-м участке, остальные без изменений. 4-я итерация – табл. 4.14, 4.15. Исходное: 3-й шаг – увеличиваем резерв только на 3-м участке, остальное без изменений. Каналы 1, 2, 2, 2, 1. 4-й шаг – опять увеличиваем резервы, в том числе и на 3-м. Получаем 3, 3, 3, 3, 2.

Таблица 4 . 1 4 Третья итерация задачи Б (окончание)

Таблица 4 . 1 5

Определение наиболее выигрышного участка для 3-й итерации задачи Б (окончание)

(δi4 )* = δ54 , значит, очередной элемент надо добавить на 5-м участке. Следовательно, ССНдляшагаj = 4 будетиметьвид(рис. 4.25):

Рис. 4.25. ССН для 4-й и последней итерации увеличения вероятности безотказной работы

164

Pс4 = 0,9·0,9375·0,9676·0,96·0,99 = 0,776.

Стоимость реализации системы на 4-м шаге оптимизации

Wс4 = Wс3 + W5 = 118 < Wсзад .

При следующих шагах значение Wс гарантированно выйдет

за допустимые пределы.

Итак, максимальное значение Pc(t) = 0,776 при стоимости реализации системы Wс = 118 меньше заданной 120. Значение небольшое, но прибыль существенная.

165

5. ТЕОРИЯ АВТОМАТОВ

Теория автоматов – раздел дискретной математики и математической кибернетики, изучающий математические модели преобразователей дискретной информации, называемые автоматами. Такими преобразователями являются как реальные устройства (вычислительные машины, автоматы, живые организмы и т.д.), так

иабстрактные системы (математические машины, аксиоматические теории и т.д.) [5].

Теория автоматов возникла в середине ХХ века с изучением конечных автоматов как математических моделей нервных систем

ивычислительных машин. Она тесно связана с теорией алгоритмов, в частности с теорией абстрактных машин, поскольку автоматы можно рассматривать как частный случай последних.

Автомат можно охарактеризовать как устройство, имеющее входной и выходной каналы и находящееся в каждый дискретный момент в одном из внутренних состояний. По входному каналу в такие моменты поступают сигналы-воздействия. В те же моменты по выходному каналу устройство выдает в среду сигналы реакции. Так возникают алфавиты состояний входных и выходных сигналов. Законы взаимодействия букв этих алфавитов задаются двумя функциями – функцией переходов и функцией выходов, отображающих пары «состояние – выходная буква» в состояния и выходные буквы соответственно. Входной средой для автомата является множество слов во входном алфавите, а внутренней и выходной средами являются множества слов в алфавитах состояний и выходном.

Автомат побуквенно перерабатывает слова из входной среды в слова двух других сред. Эта переработка носит название «поведение автомата». Указанные параметры – алфавиты и функции – своими свойствами определяют различные типы автоматов. Так, при конечности всех алфавитов получают автомат конечный, при снятии этого ограничения – автомат бесконечный.

166

При замене функций на отношения получают автоматы частичные и недетерминированные, при допущении случайных функций приходят к автомату вероятностному. При интерпретации входной среды термами или графами приходят к автоматам над термами и автоматам в лабиринтах и т.п. Большинство задач – общие для основных видов управляющих систем. К ним относятся задачи анализа и синтеза автоматов, задачи полноты, минимизации, эквивалентных преобразований автоматов и др.

Задача анализа состоит в том, чтобы по заданному автомату описать его поведение или по неполным данным об автомате и его функционировании установить те или иные его свойства. Задача синтеза автоматов состоит в построении автомата с наперед заданным поведением или функционированием. К этой задаче примыкают проблемы, связанные с оценкой сложности автоматов, обладающих заданным поведением, а также с построением алгоритмов, дающих в определенном смысле оптимальные автоматы.

Кроме того, применительно к классам исходных автоматов или автоматных отображений возникает проблема полноты. Задача эквивалентных преобразований ставится как для автоматов, так и для различных заданий их поведения. Помимо перечисленных постановок задач, общих для многих управляющих систем, в теории автоматов имеются специфические проблемы.

Так, в зависимости от условий задачи поведение автоматов удобно задавать на разных языках (регулярные выражения, канонические уравнения, язык логики предикатов и т.д.), в связи с чем важными задачами являются выбор достаточно удобного адекватного языка и перевод с одного языка на другой. В тесной связи с задачами синтеза и эквивалентных преобразований находится задача минимизации числа состояний автомата, а также получения соответствующих оценок. Для конечных автоматов выработаны достаточно простые алгоритмы, позволяющие по регулярным выражениям получать автоматы, представляющие соответствующие события и имеющие минимально возможное число состояний. Близкий круг вопросов возникает в связи с моделированием пове-

167

дения автоматов одного класса автоматами другого класса. Представляют интерес вопросы минимизации моделирующих автоматов

иоценки их сложности. Например, при переходе от недетерминированного автомата, представляющего регулярное множество слов, к конечному автомату, представляющему это же множество, число состояний может возрастать как показательная функция.

Специальный раздел связан с так называемыми экспериментами с автоматами. Основная задача здесь состоит в том, чтобы получить определенные сведения о строении автомата путем наблюдения его реакции на те или иные внешние воздействия. При этом возникает большой круг задач, связанный с классификацией экспериментов

ис вопросами разрешимости задач определенными видами экспериментов, а также с оценками длин минимальных экспериментов, достаточных для решения тех или иных задач. Понятие эксперимента с автоматами используется также в задачах контроля автоматов.

При изучении коллективов и игр автоматов, поведения автоматов в случайной среде рассматриваются вопросы взаимодействия автоматов друг с другом или с определенными внешними средами.

5.1. ЭКВИВАЛЕНТНОСТЬ АВТОМАТОВ. ТЕОРЕМА МУРА

Цепочки входных символов

Пусть ∑ – алфавит, конечное множество входных символов Х автомата [11].

∑* – множество цепочек из алфавита ∑. Будем использовать символ пустой цепочки λ – не содержащей символов. Введем операцию конкатенации (склеивания) цепочек: . Тогда ааb bа = ааbаb.

Знак конкатенации часто не указывают. Цепочки обычно обозна-

чают малымигреческимибуквами: α, β, ν, ….

Очевидно, чтопустаяцепочка λ является каклевой, таки правой единицейв алгебраическом смысле: α λ = λ α = α.

168

Расширенные функции переходов и выходов

Пусть A = < X , Y , Z , y0 , φ, ψ > – конечный автомат. Расширенными функциями переходов и выходов автомата называются функции, определённые не на входных символах, а на цепочках входных символов Х*:

φ* ( y, λ) = y;φ* ( y, aα) = φ* (φ( y, a), α),

ψ* ( y, λ) = y; ψ* ( y, aα) = ψ( y, a) ψ* (φ( y, a)α).

Достижимые и недостижимые состояния автомата

Если в некоторые состояния автомата нет пути из начального состояния, то они называются недостижимыми, иначе – достижимыми. Недостижимые состояния для инициального автомата (у которого определено начальное состояние) можно удалить – они не влияют на поведение автомата.

Итак, некоторое состояние y автомата

A = < X , Y , Z , y0 , φ, ψ > .

называют достижимым тогда и только тогда, когда существует цепочка α, приводящая к нему из начального состояния:

Достижимо_ y ↔ ( α X * )[φ* (y0 =, α) y].

Состояние y автомата называют недостижимым тогда и только тогда, когда не существует цепочки α, приводящей к нему из начального состояния:

Недостижимо_ y ↔ Неверно, что( α X * )[φ* (y0 =, α) y].

169

Иначе:

Недостижимо_ y ↔ ( α X * )[φ* (y≠ ,α) y].

0

Эквивалентность автоматов

Определение. Конечные автоматы А:

A = < X A , YA , Z A , y0A , φA , ψA >

и В:

B = < X B , YB , ZB , y0B , φB , ψB >

эквивалентны в случае:

1)если их входные алфавиты совпадают: X A = X B = X ,

2)реализуемые ими отображения совпадают:

( α X * )[ψ*A (y0A , α=) ψ*Β (y0B , α)].

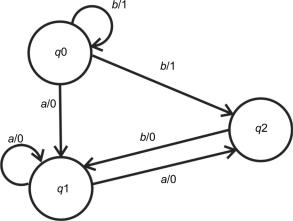
Пример [11]. Два конечных автомата А (рис. 5.1) и В (рис. 5.2) имеютразноечисло состоянийионипо-разному называются.

Автомат А:

Рис. 5.1. Некоторый автомат А

170