Дискретная математика & математическая логика
..pdf

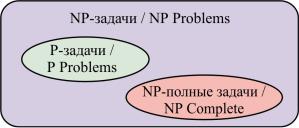
Рис. 9.2. Классы сложности при условии P ≠ NP
Эвристические алгоритмы
Одним из путей к решению NP-полных задач является разработка приближённых, эвристических алгоритмов.
В эвристических алгоритмах используют для этого некоторую дополнительную информацию – эвристики, позволяющие находить решения, лишь на 10–15 % хуже оптимальных. Эвристики – совокупности разумных соображений, использование которых предположительно позволяет получить решение, близкое к оптимальному.
Тем не менее NP-сложные задачи не имеют гарантированных оценок времени решения. Даже незначительное изменение исходных данных приводит к его резкому увеличению.
Генетические алгоритмы
В настоящее время активно развивается направление так называемых генетических алгоритмов («эволюционных вычислений»). Это направление использует в борьбе с перебором вариантов опыт развития природы и человека. При этом применяется и соответствующая терминология: «популяция» – некоторое множество вариантов; «скрещивание» вариантов путем определенного комбинирования «хромосом особей» из исходной популяции и получение «потомков»; «эволюция» сцельюполучениялучшихрешений(см. подразд. 4.5).
244