
Дискретная математика & математическая логика
..pdf
мат из состояния 8, поскольку оно единственное в π2 и дальше дробиться не будет. Получаем табл. 5.3:
|
|
|
|
|
|
|
|
Таблица |
5 . 3 |
||||||||
|
|
Таблица переходов из разбиения π2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ y(t) |
|
Функции переходов и выходов |
|
|
|
π2 |
|
|
|
|
|||||||
|
ϕ y(t + 1) |
ψ z(t) |
|
|
ϕ y(t + 1) |
|
|
|
|
|
|||||||
|
а |
|
b |
а |
|
b |
|
а |
|
|
b |
|
π3 |
|
|||
1 |
3 |
|
6 |
1 |
|
0 |
|
С2 |
|
|
А2 |
|
А3 |
|
|
||
2 |
4 |
|
8 |
0 |
|
1 |
|
В2 |
|
|
D2 |
|
В3 |
|
|
||
3 |
1 |
|
4 |
1 |
|
0 |
|
А2 |
|
|
В2 |
|
|
D3 |
|
|
|
4 |
7 |
|
9 |
0 |
|
1 |
|
В2 |
|
|
С2 |
|
|
С2 |
|
|
|
5 |
9 |
|
1 |
1 |
|
0 |
|
С2 |
|
|
А2 |
|
|
А3 |
|
|
|
6 |
3 |
|
5 |
1 |
|
0 |
|
С2 |
|
|
А2 |
|
|
А3 |
|
|
|
7 |
4 |
|
3 |
0 |
|
1 |
|
В2 |
|
|
С2 |
|
|
С2 |
|
|
|
8 |
4 |
|
2 |
1 |
|
0 |
|
В2 |
|
|
В2 |
|
Е3 |
|
|
||
9 |
5 |
|
7 |
1 |
|
0 |
|
А2 |
|
|
В2 |
|
D3 |
|
|
||
Получаем разбиение
π3 = {А3 = <1, 5, 6>; В3 = <2>; С3 = <4, 7>; D 3 = <3, 9>; Е3 = <8>}.
Строим таблицу переходов из разбиения π4 (табл. 5.4):
|
|
|
|
|
|
|
|
Таблица |
5 . 4 |
||||||
|
|
Таблица переходов из разбиения π4 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ y(t) |
|
Функции переходов и выходов |
|
|
|
π4 |
|
|
|||||||
|
ϕ y(t + 1) |
ψ z(t) |
|
|
ϕ y(t + 1) |
|
|
|
|||||||
|
а |
|
b |
а |
|
b |
|
а |
|
|
b |
|
|
|
|
1 |
3 |
|
6 |
1 |
|
0 |
|
D3 |
|
|
А3 |
|
|
А4 |
|
2 |
4 |
|
8 |
0 |
|
1 |
|
С3 |
|
|
Е3 |
|
|
В4 |
|
3 |
1 |
|
4 |
1 |
|
0 |
|
А3 |
|
|
С3 |
|
|
С4 |
|
4 |
7 |
|
9 |
0 |
|
1 |
|
С3 |
|
|
D3 |
|
|
D4 |
|
5 |
9 |
|
1 |
1 |
|
0 |
|
D3 |
|
|
А3 |
|
|
А4 |
|
6 |
3 |
|
5 |
1 |
|
0 |
|
D3 |
|
|
А3 |
|
|
А4 |
|
7 |
4 |
|
3 |
0 |
|
1 |
|
С3 |
|
|
D3 |
|
|
D4 |
|
8 |
4 |
|
2 |
1 |
|
0 |
|
С3 |
|
|
В3 |
|
|
Е4 |
|
9 |
5 |
|
7 |
1 |
|
0 |
|
А3 |
|
|
С3 |
|
|
С4 |
|
181
Получаем разбиение
π4 = {А4 = <1, 5, 6>; В4 = <2>; С4 = <4, 7>; D 4 = <3, 9>; Е4 = <8>}.
π4 = π3, искомое разбиение найдено.
Минимальный автомат имеет 5 состояний, а его функции переходов и выходов определяются так (берём за основу разбиение π3):
ϕ(А3, а) = D3, ψ(А3, а) = 1 и т.д.
5.3.АВТОМАТЫ МИЛИ И МУРА
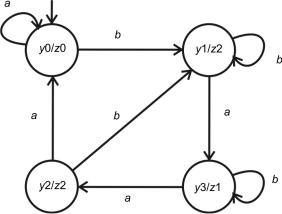
Пример конечного автомата Мура представлен на рис. 5.11 [11]. Выход автомата однозначно зависит только от значения входного сигнала.
Например, в состояние у1 можно попасть по трём переходам: из состояния у0 под воздействием b, из состояния у1 под воздействием b, из состояния у2 также под воздействием b.
Рис. 5.11. Автомат Мура
Очевидно, что каждому автомату Мура можно построить эквивалентный автомат Мили (рис. 5.12). Выходы автомата Мили за-
182
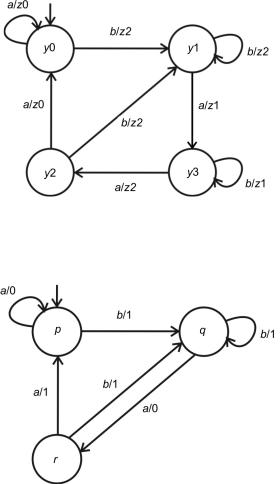
висят не только от значений входов, но и от состояния автомата в предыдущий момент времени.
Рис. 5.12. Эквивалентный автомат Мили
Не так очевидно обратное утверждение: каждому автомату Мили соответствует эквивалентный автомат Мура (рис. 5.13).
Рис. 5.13. Некоторый автомат Мили
Каждое состояния автомата Мили расщепляется на несколько эквивалентных, с каждым из которых связывается один выходной сигнал (рис. 5.14).
183
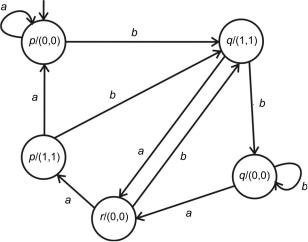
Рис. 5.14. Эквивалентный автомат Мура
5.4.РЕАКТИВНЫЕ СИСТЕМЫ
Впоследнее время для инженеров и исследователей, работающих в области информатики, стала ясна необходимость выделения особого класса систем, которые были названы «реактивными»
или «реагирующими» системами (reactive system) [11]. Это системы, взаимодействующие с окружением и реагирующие на поток внешних событий. Как правило, реактивные системы состоят из нескольких подсистем, и взаимодействие подсистем является частью взаимодействия системы с ее окружением. Например, это микрокалькулятор, система управления прохождения метро. Автоматная модель является удобным средством описания таких систем. Однако классическое графическое представление конечных автоматов страдает рядом недостатков. Главным недостатком является отсутствие параметров, в частности отсутствие понятия времени. Другие недостатки – отсутствие иерархии сосстояний, обобщения переходов, средств выражения прерываний и продолжения нормальной работы после их обработки.
184
Расширением модели классического автомата является введение понятия «внешнее событие», наступление которого можно считать условием перехода автомата из состояния и состояние. Например, событие срабатывания таймера. С этим типом событий естественно связывается понятие времени в автомате. Действительно, введение понятия времени проще всего связать с ограничением времени пребывания автомата в конкретном состоянии и такое ограничение задать таймером. Событие срабатывания таймера вызовет переход автомата в другое состояние.
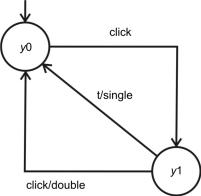
Рис. 5.15. Задача спецификации процесса
Рассмотрим и качестве примера задачу спецификации процесса, определяющего одинарный либо двойной щелчок мыши (рис. 5.15). Двойным щелчком считается пара нажатий на клавишу мыши, разделяемая менее чем τ = 250 мс. На рисунке представлен граф переходов автомата, решающего эту задачу. По первому щелчку мыши автомат переходит в состояние S1, и если до истечения следующих τ = 250 мс на вход автомата поступит еще один сигнал-событие сliск, то на выход будет выдан сигнал double, в противном случае – сигнал single.
185

5.5. КОЛЛЕКТИВЫ АВТОМАТОВ
Коллективы автоматов– множество взаимодействующих для решения общей задачи автоматов [9]. Эта область теории автоматов связа-
насименемМихаилаЛьвовичаЦетлина(1924–1966) – рис. 5.16:
Рис. 5.16. Михаил Львович Цетлин
Это яркий представитель плеяды отечественных ученых, создавших школу кибернетики в нашей стране. М.Л. Цетлин открыл но-
вое научное направление – коллективное поведение автоматов,
которое сейчас во многом определяет перспективные пути развития систем искусственного интеллекта; его работы в этой области представляют интерес не только для биологии и теории автоматов, но и для социологии. Начиная с 1961 года и до конца жизни М.Л. Цетлин напряженно занимался проблемами целесообразного поведения автоматов. Начав с простейших моделей поведения (по его любимому выражению, «маленького животного в большом мире»), он предложил конструкцию автомата, минимизирующего число неблагоприятных воздействий внешнего мира. В последующие годы М.Л. Цетлин рассматривал более сложные модели поведения, в частности поведение автомата в изменяющейся среде, где автомат вынужден непрерывно переучиваться.
186
Стратегия поведения каждого автомата определялась выигрышем всех, а выигрыш коллектива определялся как сумма выигрышей каждого.
Однородные среды
Системы распределенной обработки информации представляют собой воплощение идеи создания так называемых однородных сред (клеточных автоматов), предложенных Э.В. Евреиновым в 60-е годы. В начале предполагалось, что элементы таких сред – элементарные конечные автоматы [12].
В 1978 году были предложены так называемые систолические матрицы для высокоскоростной числовой обработки, содержащие множество простейших распределенных арифметических элементов. Они, например, применяются для умножения матрицы на вектор (последовательный ряд арифметических элементов), причем на вход ряда последовательно подаются элементы вектора, а в каждый элемент подаются элементы матрицы.
По мере развития интегральной технологии элементарные процессоры однородных сред постоянно усложнялись, что привело к созданию в 80-е годы ХХ века нового микроэлектронного прибора, называемого транспьютером.
Транспьютер – это высокопроизводительный микрокомпьютер с развитыми средствами связи с другими аналогичными микрокомпьютерами, предназначенный для построения однородной среды из десятков, сотни и даже тысяч подобных компонентов. Транспьютеры применяются, например, в задачах обработки изображений, распознавания образов.
Клеточный автомат
Клеточный автомат – набор клеток, образующих некоторую периодическую решетку с заданными правилами перехода, определяющими состояние клетки в следующий момент времени через состояние клеток, находящихся от неё на расстоянии не больше не-
187

которого, в текущий момент времени. Как правило, рассматриваются автоматы, где состояние определяется самой клеткой и ближайшими соседями. В качестве решётки обычно рассматривается кубическая решётка. Один из самых интересных примеров клеточного автомата – игра «Жизнь».
Джон Конвей (род. 1937) – рис. 5.17 – заинтересовался проблемой, предложенной в 1940-х годах известным математиком Джоном фон Нейманом, который пытался создать гипотетическую машину, которая может воспроизводить сама себя. Джону фон Нейману удалось создать математическую модель такой машины с очень сложными правилами.
Рис. 5.17. Джон Конвей
Конвей попытался упростить идеи Неймана и ему удалось создать правила, которые стали правилами игры «Жизнь» (рис. 5.18).
Место действия этой игры – « вселенная» – это размеченная на клетки поверхность – безграничная, ограниченная или замкнутая. В компьютерных реализациях игры чаще всего используют поверхность тора. Каждая клетка на этой поверхности может находиться в двух состояниях: быть живой или мёртвой. Клетка имеет восемь соседей.
188
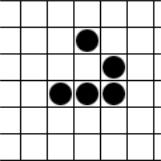
Рис. 5.18. Игра «Жизнь»
Распределение живых клеток в начале игры называется первым поколением. Каждое следующее поколение рассчитывается на основе предыдущего по таким правилам: пустая (мёртвая) клетка ровно с тремя живыми клетками-соседями оживает; если у живой клетки есть две или три живые соседки, то эта клетка продолжает жить;
впротивном случае (если соседок меньше двух или больше трёх) клетка умирает (от «одиночества» или от «перенаселённости»). Игрок не принимает прямого участия в игре, а лишь расставляет «живые» клетки, которые взаимодействуют согласно правилам уже без его участия. Эти простые правила приводят к огромному разнообразию форм, которые могут возникнуть в игре.
Вскоре после опубликования правил было обнаружено несколько интересных шаблонов (вариантов расстановки живых клеток
впервом поколении), в частности: r-пентамино и глайдер. Некоторые такие фигуры остаются неизменными во всех по-
следующих поколениях, состояние других периодически повторяется, в некоторых случаях со смещением всей фигуры. Существует фигура (diehard) всего из семи живых клеток, потомки которой существуют в течение 130 поколений, а затем исчезают.
Конвей первоначально предположил, что никакая начальная комбинация не может привести к неограниченному размножению, и предложил премию 50 долл. тому, кто докажет или опровергнет эту гипотезу.
189
Приз был получен группой из Массачусетсского технологического института, придумавшей неподвижную повторяющуюся фигуру, которая периодически создавала движущиеся глайдеры. Таким образом, количество живых клеток могло расти неограниченно. Затем были найдены движущиеся фигуры, оставляющие за собой «мусор» из других фигур.
К настоящему времени сложилась следующая классификация фигур:
–устойчивыефигуры: фигуры, которыеостаютсянеизменными;
–периодические фигуры: фигуры, у которых состояние повторяется через некоторое число поколений;
–двигающиеся фигуры: фигуры, у которых состояние повторяется, но с некоторым смещением;
–« ружья»: фигуры, у которых состояние повторяется, но дополнительно появляется двигающаяся фигура;
–« паровозы»: двигающиеся фигуры, которые оставляют за собой следы в виде устойчивых или периодических фигур;
–« пожиратели»: устойчивые фигуры, которые могут пережить столкновения с некоторыми двигающимися фигурами.
Пороговая логика
В 1943 году Уоррен Мак-Каллок и Уолтер Питтс предложили модель формального нейрона как переключательной функции.
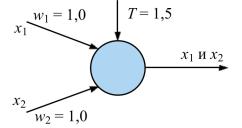
Каждый вход (синапс) хi учитывается с некоторым весом wi
(рис. 5.19).
Рис. 5.19. Схема нейрона, настроенного на моделирование логического И
190
