Дискретная математика & математическая логика

Поиск эйлерова цикла в графе

Будем рассматривать самый общий случай – случай ориентированного мультиграфа, возможно, с петлями. Мы предполагаем, что эйлеров цикл в графе существует и состоит хотя бы из одной вершины. Для поиска эйлерова цикла воспользуемся тем, что эйлеров цикл – это объединение всех простых циклов графа. Следовательно, наша задача – эффективно найти все циклы и эффективно объединить их в один.

Реализовать это можно, например, так, рекурсивно:

procedure find_all_cycles (v) var массив cycles

1.Пока есть цикл, проходящий через v, находим его, добавляем все вершины найденного цикла в массив cycles (сохраняя порядок обхода), удаляем цикл из графа.

2.Идем по элементам массива cycles, каждый элемент cycles[i] добавляем к ответу, из каждого элемента рекурсивно вызываем себя: find_all_cycles (cycles[i]). Достаточно вызвать эту процедуру из любой неодиночной вершины графа, и она обязательно найдет все циклы в графе, удалит их из графа и объединит их

водин эйлеров цикл. Для поиска цикла на шаге 1 используем поиск

вглубину.

Сложность полученного алгоритма равна O(M), т.е. линейна относительно количества ребер М в данном графе.

Гамильтонов граф

Гамильтонов граф в теории графов [3] – это граф, содержащий гамильтонову цепь или гамильтонов цикл.

Гамильтонова цепь – цепь, содержащая каждую вершину графа точно один раз. Гамильтонова цепь, начальная и конечная вершины которой совпадают, носит название гамильтонов цикл. Гамильтонов цикл является простым основным циклом.

101

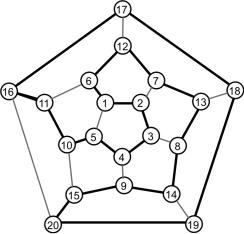
Гамильтоновы цепь, цикл и граф названы в честь ирландского математика У. Гамильтона, который впервые определил эти классы, исследовав задачу «кругосветного путешествия» по додекаэдру, узловые вершины которого символизировали крупнейшие города Земли, а рёбра – соединяющие их дороги (рис. 3.30).

Рис. 3.30. Гамильтонов граф

Условия существования гамильтонова цикла

Условие Дирака (1952). Пустьp – число вершин в данном графе. Если степень каждой вершины не меньше, чем p / 2 , то граф называ-

етсяграфом Дирака. ГрафДиракаотносится кгамильтоновым. Условие Оре (1960). Пусть p – количество вершин в данном

графе. Если для любой пары несмежных вершин x, y выполнено неравенство d (x) + d ( y) ≥ p , то граф называется графом Оре (сумма

степеней любых двух несмежных вершин не меньше общего числа вершин в графе). Граф Оре также гамильтонов.

Доказана теорема Бонди – Хватала, обобщающая утверждения Дирака и Оре. Вначале определим замыкание графа.

102

Пусть у графа Gn вершин. Тогда замыкание cl(G) однозначно строится по G добавлением для всех несмежных вершин u и v, у которых выполняется degree(v) + degree(u) ≥ n нового ребра uv. Граф является гамильтоновым тогда и только тогда, когда его замыкание – гамильтонов граф.

Решение задачи связано с существенным перебором вариантов и может быть найдено, например, методом генетического алгоритма, который обсуждается далее.

3.8. АНАЛИЗ ГРАФА МАРКОВСКОЙ ЦЕПИ

Марковские процессы

Рис. 3.31. Андрей Андреевич Марков

(1856–1922)

Андрей Андреевич Марков – выдающийся русский математик, внёсший большой вклад в теорию вероятности, математический анализ и теорию чисел – рис. 3.31. Академик Санкт-Петер- бургской Императорской Академии наук. В 1912 году математик подвергся отлучению от церкви, после того как написал, что не ус-

103

матривает разницы между иконами и идолами. Отец А.А. Марковамладшего – выдающегося советского математика – рис. 3.32.

Рис. 3.32. Андрей Андреевич Марков

(1903–1979)

Нормальный алгорифм Маркова – один из стандартизованных вариантов представления об алгорифме (алгоритме). Понятие нормального алгорифма введено А.А. Марковым в конце 1940-х годов. Это относится к теории алгоритмов, изучаемых в математической логике. Марковские процессы, марковские графы (цепи) – это А.А. Марков-старший.

Пример марковского графа [8]

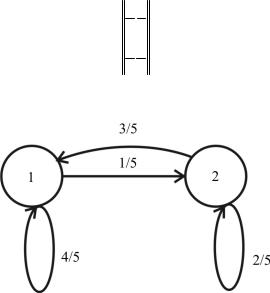
Пустьнекоторая фирма может быть в двухсостояниях: 1 – спрос на продукцию есть, 2 – спроса нет. С течением времени рынок изменяется так, что имеется вероятность 4/5, что фирма останется в состоянии 1. Если фирма оказывается в состоянии 2, то она принимает меры к улучшению продукции и с вероятностью 3/5 к концу года перейдёт всостояние 1. Тогдаматрицапереходовимеетвид

104

41

55

32

55

АцепьМарковаилиграфмарковскойцепиимеетвид– рис. 3.33.

Рис. 3.33. Граф марковской цепи

Обозначим вероятность нахождения системы на i-м шаге в состоянии j πij , а вероятность перехода из j-го состояния в k-е: p jk .

Тогда для первого шага марковского процесса, если начальное состояние 1 (шаг 0),

Для второго шага

105

Продолжим расчёты и получим таблицы – табл. 3.3, 3.4:

Таблица 3 . 3

Вероятности состояний при начальном состоянии 1 для 5 шагов марковского процесса

Таблица 3 . 4

Вероятности состояний при начальном состоянии 2 для 5 шагов марковского процесса

Если в марковской цепи существует предельное распределение вероятностей при n → ∞ и не зависящее от начального состояния, то это определяет установившийся режим системы.

Такая система называется статически устойчивой, а марковский процесс – эргодическим. Переход к эргодическому процессу – переходный процесс.

Марковская цепь – ориентированный граф, нагруженный вероятностями (или интенсивностями) переходов из состояния в состояние.

106

Пусть задана система, которая может находиться в двух состояниях: состояние 1 – состояние работоспособности, состояние 2 – состояние отказа(рис. 3.34).

Рис. 3.34. Пример марковской цепи

Заданы интенсивности переходов из состояния в состояние – параметром потока отказов ω = const (переход в состояние отказа 2) и интенсивность восстановления µ (переход в состояние работоспособности после ремонта).

По графу марковской цепи строится система алгебраических уравнений для установившегося режима путем анализа входящих и исходящих дуг, т.е. сумма меток входящих и исходящих дуг равна нулю:

0 = −P (t)ω+ P (t)µ,

1 2

1 = P (t) + P (t).

1 2

Второе уравнение определяет равенство единице суммы вероятностей всех состояний. Метка дуги является произведением вероятности соответствующегосостояния, из которогодугаисходит, на интенсивностьэтойдуги.

Далее для определения вероятностей состояний решается система уравнений

0 = −(1− P2 (t))ω+ P2 (t)µ, ω= P2 (t)[ω+ µ],

P2 (t) = ωω+ µ ,

107

Коэффициент готовности – это вероятность нахождения в состоянии 1:

гдеТо – времянаработкина отказ; Тв – среднее времявосстановления. Время восстановления определяется как

Тв = Тобнаружения + Тлокализации + Тзамены.

Таким образом, чем меньше отношение интенсивности отказов к интенсивности восстановления, тем более коэффициент готовности приближается к 1.

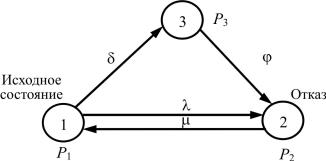
Рассмотрим марковскую модель, где одна из трех вершин представляет собой состояние отказа, т.е. вводится дополнительное работоспособное состояние (рис. 3.35).

Рис. 3.35. Граф марковского процесса для одного дополнительного состояния готовности Р3

Решение соответствующей системы алгебраических уравнений Колмогорова для установившегося режима может быть получено аналитически:

108

и позволяет получить коэффициент готовности – сумму вероятностей работоспособных состояний:

kг = р1 + р2 .

Выразим из второго уравнения p2 через p1:

р2 = δφр1 .

Получим из третьего уравнения

р3 = 1 − р1 − р2 .

Тогда р3 =1 − р1 − δφр1 .

Подставляем в первое уравнение:

(1 − р1 − δφр1 )µ = р1 (δ+ λ).

Получаем выражение для p1:

µ = µр1 + δφр1 µ + р1 (δ+ λ),

µ = р1 (µ + φδ µ + δ+ λ),

109

Сравним значения коэффициента готовности марковской цепи

(см. рис. 3.34)

К= 1

1+ µλ

скоэффициентом готовности для марковской цепи (см. рис. 3.35)

110